[每日一题]:C. Frog Jumps -- 二分

饭前点心:

  之前做过的一道题，当时做的时候一把过了，这次竟然想不起来了，唉，几天
  不思考，脑子锈掉了。

题目:

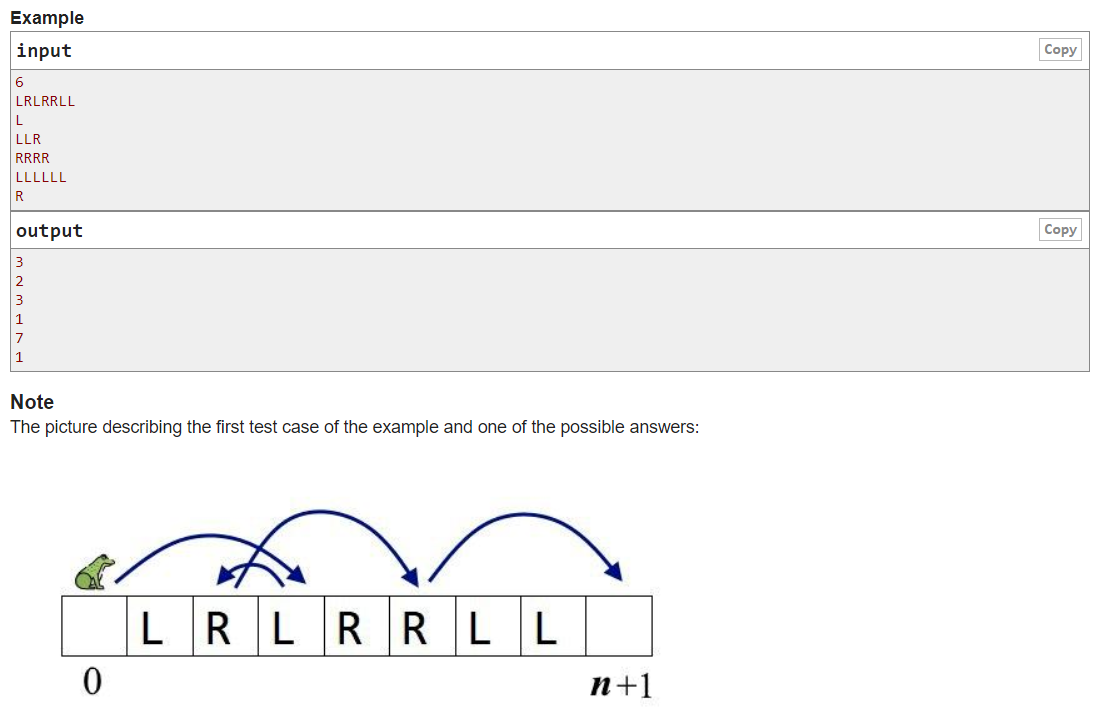
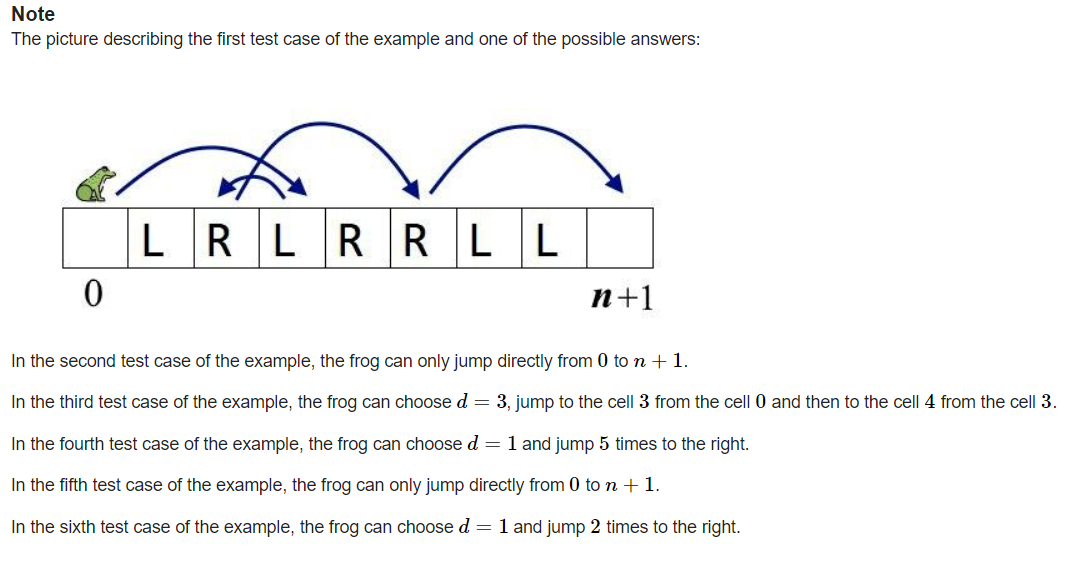
题目大意:

  找到一个最小值,满足按照序列给的方式走到终点。

侃侃：

  题目说一定存在这样一个值,而且是找一个最小值,显然这个最小值一定在
  1 ~ n + 1 之间,满足单调性,我们就可以二分了,假设某个值成立带进去
  看是否能走到终点,这个时候我们就需要去判断什么时候是一定能走到终点
  的,如果说所有 R 之间的距离都是 <= d 的,那么一定是可以走到终点的,
  能走到终点时说明可能还存在比假设的 d 更小的值存在,则 r = mid;
  否则 l = mid + 1;

Code:

#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = 2e5 + 10;

char a[maxn];

int t,len;

bool Check(int x) {
	bool flag = true;
	int idx = 0,ans;
	for(int i = 1; i <= len; i ++) {
		if(a[i] == 'R') {
			ans = i - idx;
			idx = i;
			// 假设的值如果成立必然满足任意两个相邻的 R 之间距离 <= x 
			if(ans > x) {
				return false;
			}
		}
	}
	// 边界需要特殊处理 
	if(idx + x >= len + 1) return true;
	else return false; 
}

int main(void) {
	scanf("%d",&t);
	while(t --) {
		scanf("%s",a + 1);
		len = strlen(a + 1);
		int l = 1,r = len + 1;
		while(l < r) {
			int mid = l + r >> 1;
			if(Check(mid)) r = mid;
			else l = mid + 1;
		}
		printf("%d
",r);
	}
	return 0;	
}