leetcode 121. Best Time to Buy and Sell Stock

leetcode 121. Best Time to Buy and Sell Stock

相关链接

leetcode

描述

  Say you have an array for which the ith element is the price of a given stock on day i.

  If you were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock), design an algorithm to find the maximum profit.

Note that you cannot sell a stock before you buy one.

Example 1:

Input: [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Not 7-1 = 6, as selling price needs to be larger than buying price.
Example 2:

Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

解决方法

solution1 one-pass

使用样例1给出的数据进行分析:

[7, 1, 5, 3, 6, 4]

我把所有数字绘成折线图:

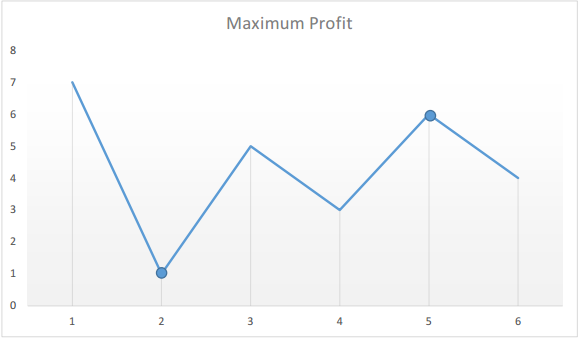
图片出处【LeetCode】
  我们需要关注谷底和顶峰，我只需要找出最低的谷底和其后面的一个最高顶峰。我们可以使用两个变量 minPrice和maxProfit来记录最低价和最大利润，遍历vector的时候，如果价格比当前的最低价格低，则替换最低价格，如果价格高于最低价格，计算利润，如果利润大于maxProfit则替换。

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        if(n == 0)
            return 0;

        int maxProfit = 0;
        int minPrice = 1000000;

        for(int i = 0; i < n; i++)
        {
            if( prices[i] < minPrice)
                minPrice = prices[i];
            else if (prices[i] - minPrice > maxProfit)
                maxProfit = prices[i] - minPrice;
        }
        return maxProfit;
    }
};

分析：时间复杂度O(N)
空间复杂度O(1)

solution2 暴力解法

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        if(n == 0)
            return 0;

        int maxProfit = 0;
        for(int i = 0; i < n; i++)
        {
           for(int j = i+1; j < n; j++)
               if(prices[j] - prices[i] > maxProfit)
                   maxProfit = prices[j] - prices[i];
        }
        return maxProfit;
    }
};

分析：时间复杂度O(N^2)
空间复杂度O(1)