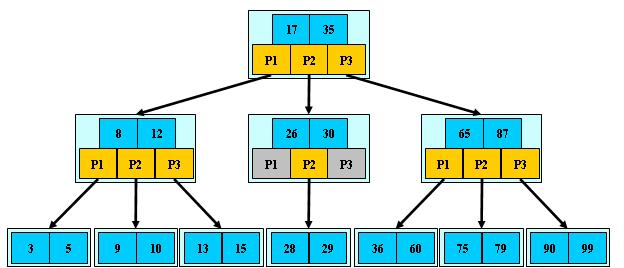
B树
如果数据装不下主存,那么这就意味着必须把数据结构放在磁盘上,此时,因为大O模型不再适应,所以导致规则发生了变化。
不平衡二叉树的最坏情形下它具有线性的深度,由于典型的AVL树接近到最优的高度,但二叉查找树不能进到低于LogN。一棵完全二叉树的高度大约为与log2N,而一棵完全M叉树的高度大约是logmN.
B树能保证少数的磁盘访问(B-树)
阶为M的B树是一棵具有下列特性的树
有关b树的一些特性,注意与后面的b+树区分:
1 关键字集合分布在整颗树中;
2 非叶节点存储直到M-1个关键字以指示搜索方向:关键字i代表子树i+1的最小的关键字
3 树和根或者是一片树叶,或者其儿子数在2到M之间
4 除根外,所有非树叶节点的儿子数在【M/2】和M之间
5 所有的树叶都在相同的深度上并有[L/2]和L之间个数据项
B树也是一种平衡的多路查找树,2-3树和2-3-4树都是B树的特例,我们把树中结点最大的孩子数目称为B树的阶,通常记为m
一棵m阶B树或为空树,或为满足如下特性的m叉树
1 树中每个结点至多有m棵子树(即至多包含m-1个关键字,两棵子树指针夹着一个关键字)
2 若根节点不是终端结点,则至少有两棵子树(至少一个关键字)
3 除根节点外的所有非叶结点只少有[m/2]棵子树。(即至少含有[m/2]-1个关键字)
4 关键字集合分布在整颗树中
有关b树的一些特性,注意与后面的b+树区分:
- 关键字集合分布在整颗树中;
- 任何一个关键字出现且只出现在一个结点中;
- 搜索有可能在非叶子结点结束;
- 其搜索性能等价于在关键字全集内做一次二分查找;
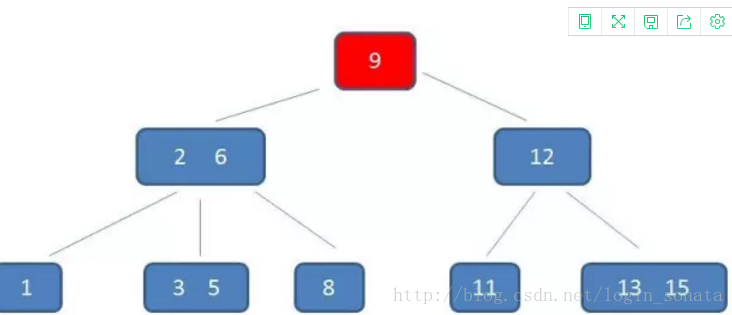
B+树

B+树和B树相比,主要的不同点在以下3项:
内部节点中,关键字的个数与其子树的个数相同,不像B树,子树的个数总比关键字个数多1个
所有指向文件的关键字及其指针都在叶子节点中,不像B树,有的指向文件的关键字是在内部节点中。换句话说,B+树中,内部节点仅仅起到索引的作用,
在搜索过程中,如果查询和内部节点的关键字一致,那么搜索过程不停止,而是继续向下搜索这个分支。
根据B+树的结构,我们可以发现B+树相比于B树,在文件系统,数据库系统当中,更有优势,原因如下:
B+树的磁盘读写代价更低
B+树的内部结点并没有指向关键字具体信息的指针。因此其内部结点相对B树更小。如果把所有同一内部结点的关键字存放在同一盘块中,那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说I/O读写次数也就降低了。
B+树的查询效率更加稳定
由于内部结点并不是最终指向文件内容的结点,而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同,导致每一个数据的查询效率相当。B+树更有利于对数据库的扫描
B树在提高了磁盘IO性能的同时并没有解决元素遍历的效率低下的问题,而B+树只需要遍历叶子节点就可以解决对全部关键字信息的扫描,所以对于数据库中频繁使用的range query,B+树有着更高的性能。
伸展树
一种自调整数据结构,它保证从空树开始连续M次对树的操作最多花费O(MlogN)时间,虽然这种保证并不排除任意单次操作花费O( N)时间的可能,而且这样的界也不如每次操作最坏情形的界为O(logN)时那么强,但是实际效果却是一样的;不存在坏的输入序列。
伸展树的摊还,当M次操作的序列总的最坏情形运行时间为O(Mf(N))时,我们就说它的摊还运行时间为O(f(N)),因此一棵伸展树每次操作的摊还代价是O(logN)。
伸展树的基本想法是:当一个节点被访问后,它就要经过一系列AVL树的旋转被推倒根上。注意,如果一个节点很深,那么在其路径上就存在许多也相对较深的节点,通过重新构造可以减少对所有这些节点的进一步访问所花费的时间。因此,如果节点过深,那么我们要求重新构造应具有平衡这棵输(到某种程度)的作用。
伸展树还不要求保留高度和平衡信息,因此它在某种程度上节省空间并简化代码(特别是当实现例程经过审慎考虑而被写出的时候)
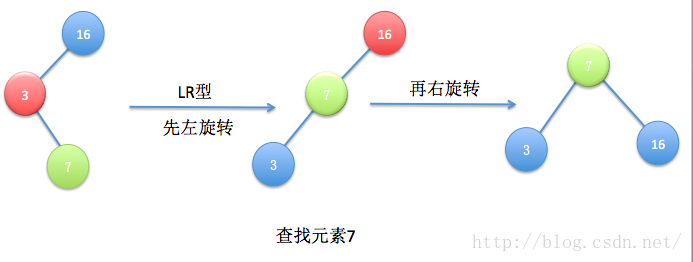
伸展树原理
伸展树的出发点是这样的:考虑到局部性原理(刚被访问的内容下次可能仍会被访问,查找次数多的内容可能下一次会被访问),为了使整个查找时间更小,被查频率高的那些节点应当经常处于靠近树根的位置。这样,很容易得想到以下这个方案:每次查找节点之后对树进行重构,把被查找的节点搬移到树根,这种自调整形式的二叉查找树就是伸展树。每次对伸展树进行操作后,它均会通过旋转的方法把被访问节点旋转到树根的位置。
为了将当前被访问节点旋转到树根,我们通常将节点自底向上旋转,直至该节点成为树根为止。“旋转”的巧妙之处就是在不打乱数列中数据大小关系(指中序遍历结果是全序的)情况下,所有基本操作的平摊复杂度仍为O(log n)。
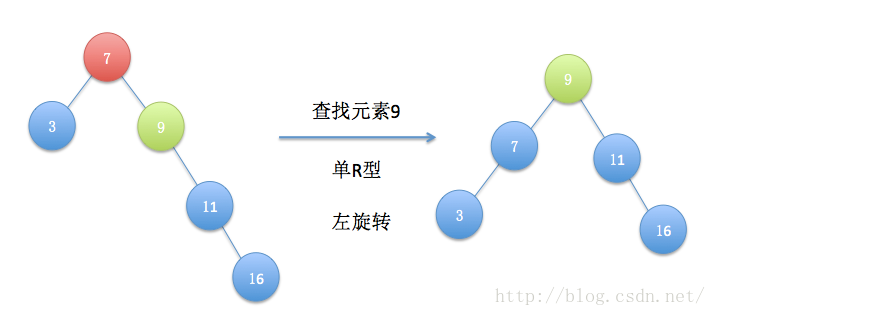
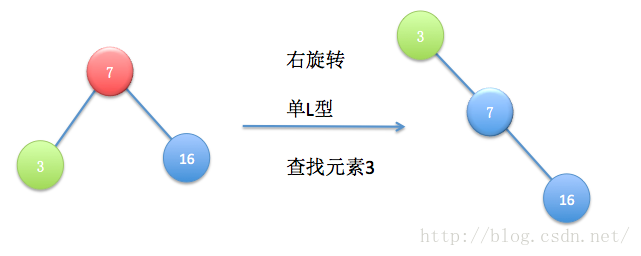
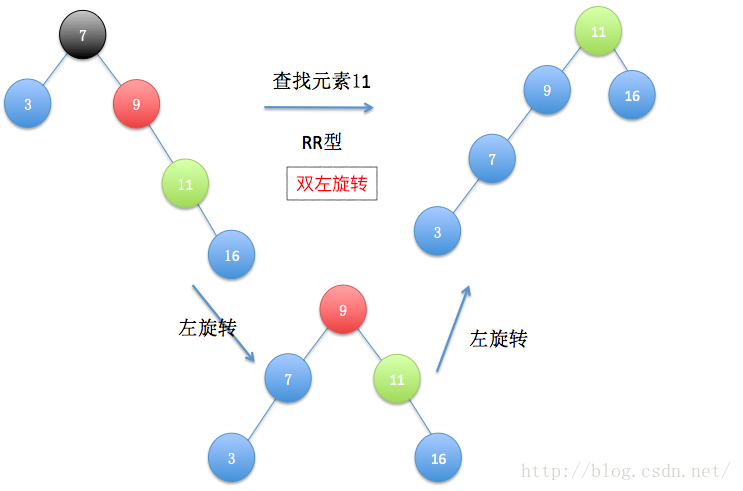
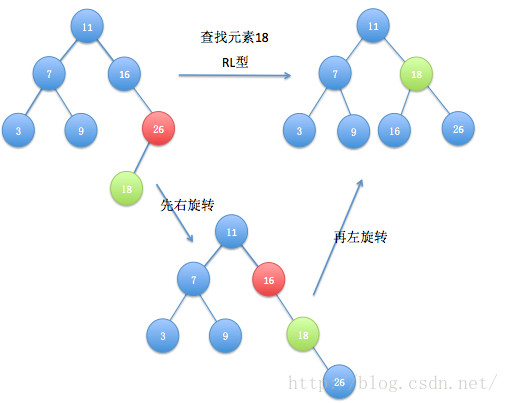
以下是伸展树的几种旋转情况