hdu--4336--概率dp

其实 概率dp最后得到的期望 你是 顺序递推 还是 逆序递推 就是取决于你对于 dp[x]这个数组是如何去定义的

这边 逆序递推的 思想 可以去看下

　　　　传送   感觉这篇博客下方的评论 讲得还可以

至于顺序递推的 可以参照下 porker给我的这个公式 

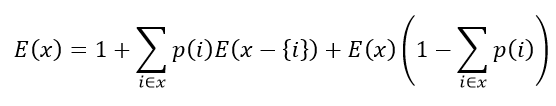
dp[x]就是表示 抽完x这个状态下所有的卡片 所需要的次数 - 所以初始化就可以定义 dp[0] = 0 了

你可以看到 当期望存在线性的递推关系的时候 我们不是按照 signma( p[i] * x[i] )来计算E(i)下的期望 而是通过 期望的状态转移来进行计算

就是说 通过算出 E(a) - > E (b)  满足该情况的p[a->b]来完成  就是上一状态通过概率为p[a->b]来实现对于目前状态的转移  当然也有一定概率p[b->b]就是还是保持原状态

我先放 逆序的代码  后面的就是顺序的代码

#include <iostream>
#include <iomanip>
using namespace std;

int n;
const int size = 25;
double p[size];
double dp[1<<size];

void solve( )
{
    double sum , sumP;
    for( int i = (1<<n)-2 ; i>=0 ; i-- )
    {
        sum = sumP = 0;
        for( int j = 0 ; j<n ; j++ )
        {
            if( ( i & (1<<j) )  )
            {
                continue;
            }
            sum += p[j] * dp[ i ^ (1<<j) ];
            sumP += p[j];
        }
        dp[i] = ( sum + 1.0 ) / sumP;
    }
}

int main()
{
    cin.sync_with_stdio(false);
    while( cin >> n )
    {
        for( int i = 0 ; i<n ; i++ )
        {
            cin >> p[i];
        }
        dp[(1<<n)-1] = 0;
        solve( );
        cout << setiosflags(ios::fixed);
        cout << setprecision(5) << dp[0] << endl;
    }
    return 0;
}

#include <iostream>
#include <iomanip>
using namespace std;

int n;
const int size = 25;
double p[size];
double dp[1<<size];

void solve( )
{
    double sum , sumP;
    for( int i = 1 ; i<=(1<<n)-1 ; i++ )
    {
        sum = sumP = 0;
        for( int j = 0 ; j<n ; j++ )
        {
            if( ( i & (1<<j) ) == 0 )
            {
                continue;
            }
            sum += p[j] * dp[ i ^ (1<<j) ];
            sumP += p[j];
        }
        dp[i] = ( sum + 1.0 ) / sumP;
    }
}

int main()
{
    cin.sync_with_stdio(false);
    while( cin >> n )
    {
        for( int i = 0 ; i<n ; i++ )
        {
            cin >> p[i];
        }
        dp[0] = 0;
        solve( );
        cout << setiosflags(ios::fixed);
        cout << setprecision(5) << dp[(1<<n)-1] << endl;
    }
    return 0;
}

他们实在很相似 就是定义与转移的区别 想起来 真的狠头痛 ..;

这边 在放一个XX论文的题目 但他那边没给出状态转移 我这边也写下

„„在2003年6月之前购买的百事任何饮料的瓶盖上都会有一个百事球星的名字。只要凑齐所有百事球星的名字，就可以参加百事世界杯之旅的抽奖活动，获取球星背包、随身听，更可以赴日韩观看世界杯。还不赶快行动！„„” 你关上电视，心想：假设有n个不同球星的名字，每个名字出现的概率相同，平均需要买几瓶饮料才能凑齐所有的名字呢？

dp[0] = 0

dp[x] = (n-x)/n*dp[x] + x/n*dp[x-1]+1

dp[x] = dp[x-1]+n/x;

dp(0)=0
dp(1)=dp(0)+n/1
dp(2)=dp(1)+n/2
.....
dp(n)=dp(n-1)+n/n

可以得到dp[n] = n * (1/1+1/2+1/3+...1/n)

或者

dp[n]=0

dp[x] = x/n*dp[x]+(n-x)/n*dp[x+1]+1

dp[x] = dp[x+1]+n/(n-x)