递归函数 原理
《数据结构》
p56
p129
小结:
1、

2、
回推+递推
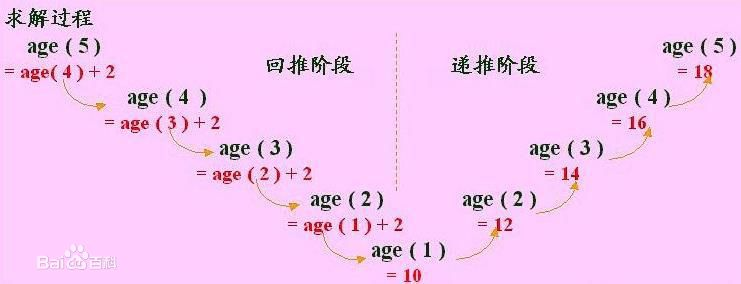
3、
程序调用自身的编程技巧称为递归( recursion)。递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。一般来说,递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时,递归前进;当边界条件满足时,递归返回。
递归,就是在运行的过程中调用自己。
构成递归需具备的条件:
函数嵌套调用过程示例
函数嵌套调用过程示例
1. 子问题须与原始问题为同样的事,且更为简单;
2. 不能无限制地调用本身,须有个出口,化简为非递归状况处理。
在数学和计算机科学中,递归指由一种(或多种)简单的基本情况定义的一类对象或方法,并规定其他所有情况都能被还原为其基本情况。
递归典型问题
梵塔问题(汉诺塔问题)
已知有三根针分别用A, B, C表示,在A中从上到下依次放n个从小到大的盘子,现要求把所有的盘子
从A针全部移到B针,移动规则是:可以使用C临时存放盘子,每次只能移动一块盘子,而且每根针上
不能出现大盘压小盘,找出移动次数最小的方案.
例2 楼梯有n阶台阶,上楼可以一步上1阶,也可以一步上2阶,编一程序计算共有多少种不同的走法.
1.求数组中的最大数
2.1+2+3+...+n
3.求n个整数的积
4.求n个整数的平均值
5.求n个自然数的最大公约数与最小公倍数
6.有一对雌雄兔,每两个月就繁殖雌雄各一对兔子.问n个月后共有多少对兔子
7.已知:数列1,1,2,4,7,13,24,44,...求数列的第 n项.
2.3典型例题
例3 快速排序
快速排序的思想是:先从数据序列中选一个元素,并将序列中所有比该元素小的元素都放到它的右边或左边,再对左右两边分别用同样的方法处之直到每一个待处理的序列的长度为1,处理结束.
def factorialA(n):
global r
print('n-factorialA', n)
if n == 0 or n == 1:
# 边界条件 出口
return
else:
r *= n
factorialA(n - 1)
def factorialB(n):
global r
print('n-factorialB', n)
if n == 0:
# 边界条件 出口
return 1
else:
rtn = n
r *= factorialB(n - 1)
return rtn
for i in range(1, 7, 1):
r = 1
factorialA(i)
print('A-{}!='.format(i), r)
r = i
factorialB(i)
print('B-{}!='.format(i), r)
def display(n):
'''
问题解法按递归算法实现。
这类问题虽则本身没有明显的递归结构,但用递归求解比迭代求解更简单,如Hanoi问题。
:param n:
:return:
'''
# 边界条件
if n > 1:
display(n - 1)
print(n, end='-')
for i in range(1, 7, 1):
print(' ', i)
display(i)
"C:Program FilesPython37python.exe" D:/ds/recursionHand.py n-factorialA 1 A-1!= 1 n-factorialB 1 n-factorialB 0 B-1!= 1 n-factorialA 2 n-factorialA 1 A-2!= 2 n-factorialB 2 n-factorialB 1 n-factorialB 0 B-2!= 2 n-factorialA 3 n-factorialA 2 n-factorialA 1 A-3!= 6 n-factorialB 3 n-factorialB 2 n-factorialB 1 n-factorialB 0 B-3!= 6 n-factorialA 4 n-factorialA 3 n-factorialA 2 n-factorialA 1 A-4!= 24 n-factorialB 4 n-factorialB 3 n-factorialB 2 n-factorialB 1 n-factorialB 0 B-4!= 12 n-factorialA 5 n-factorialA 4 n-factorialA 3 n-factorialA 2 n-factorialA 1 A-5!= 120 n-factorialB 5 n-factorialB 4 n-factorialB 3 n-factorialB 2 n-factorialB 1 n-factorialB 0 B-5!= 20 n-factorialA 6 n-factorialA 5 n-factorialA 4 n-factorialA 3 n-factorialA 2 n-factorialA 1 A-6!= 720 n-factorialB 6 n-factorialB 5 n-factorialB 4 n-factorialB 3 n-factorialB 2 n-factorialB 1 n-factorialB 0 B-6!= 30 1 1- 2 1-2- 3 1-2-3- 4 1-2-3-4- 5 1-2-3-4-5- 6 1-2-3-4-5-6- Process finished with exit code 0