往前翻几个编号相邻的题目翻到了这么一道题,感觉很好奇就做了一下
(upd:我下午问了下出题人做法,他就把题隐藏了……这不太友好啊……所以我补一下题意:)
题意
给你两个整数 $x$ 和 $y$,求 $x^y$ 和 $y^x$ 的大小关系。输出 $-1$ 表示前者大,$1$ 表示后者大,$0$ 表示一样大。
$0le xle 10^{3000}, -100le yle 10^{3000}$
题解
首先特判 $x$ 或 $y$ 为 $0$,$y=-1$ 以及 $ylt -1$ 的情况。
对于剩下的正常情况,显然幂可以取对数转化为乘数。
即把 $x^y$ 取 $ln$ 转化为 $yln{x}$,$y^x$ 取 $ln$ 转化为 $xln{y}$
然后 $x^y$ 和 $y^x$ 的大小关系等于 $yln{x}$ 和 $xln{y}$ 的大小关系
移项,可得等于 $frac{ln{x}}{x}$ 和 $frac{ln{y}}{y}$ 的大小关系
咋一看,$ln{x}$ 的变化速率显然比 $x$ 小很多啊!那我们是否可以大胆猜测,$x$ 越大,$frac{ln{x}}{x}$ 越小呢?
但我们没有给 $x$ 的定义域。
我们直觉上认为 $x$ 的定义域为 $[1,infty)$ 的整数。
但我们没有证明这个结论,下面用实践来检验一下。
我们画一下 $y=frac{ln{x}}{x}$ 的图象
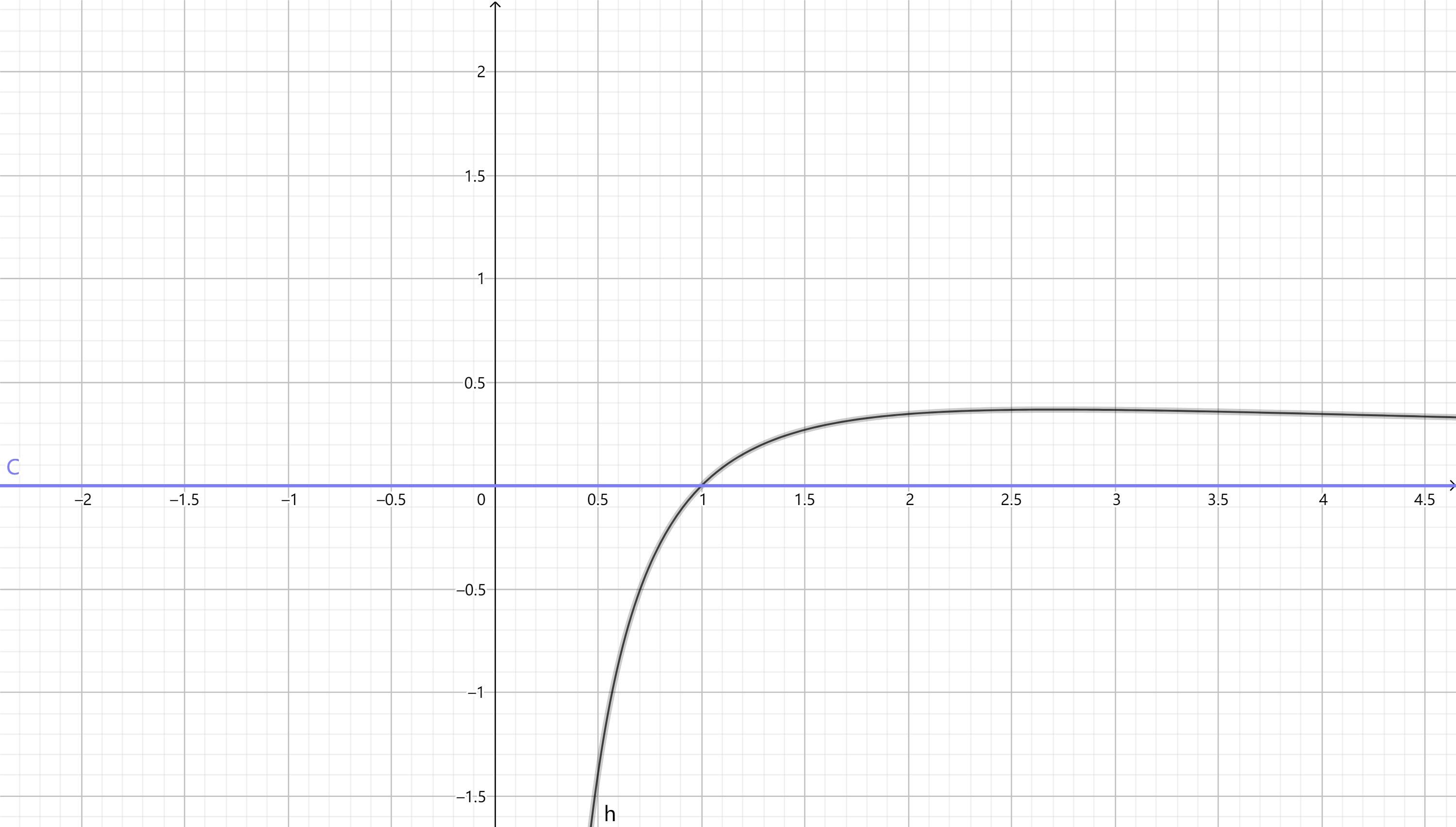
有没有观察到最高点的横坐标为 $e$?
那我们之前猜的那个结论好像就不对了
这是偶然吗?我们把 $log$ 的底数换成 $10$ 画一下看看
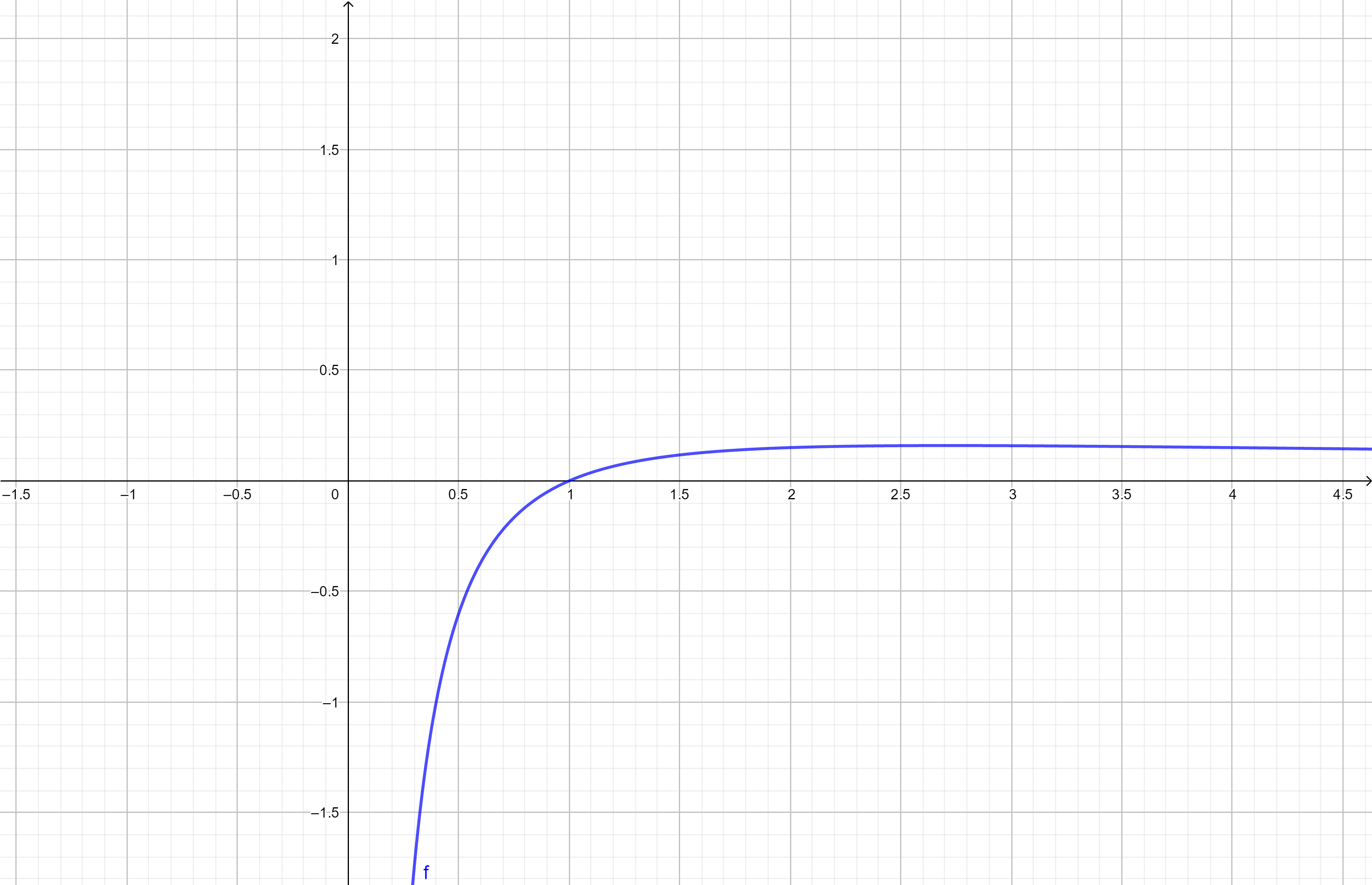
再把底数换成 $2$ 看看
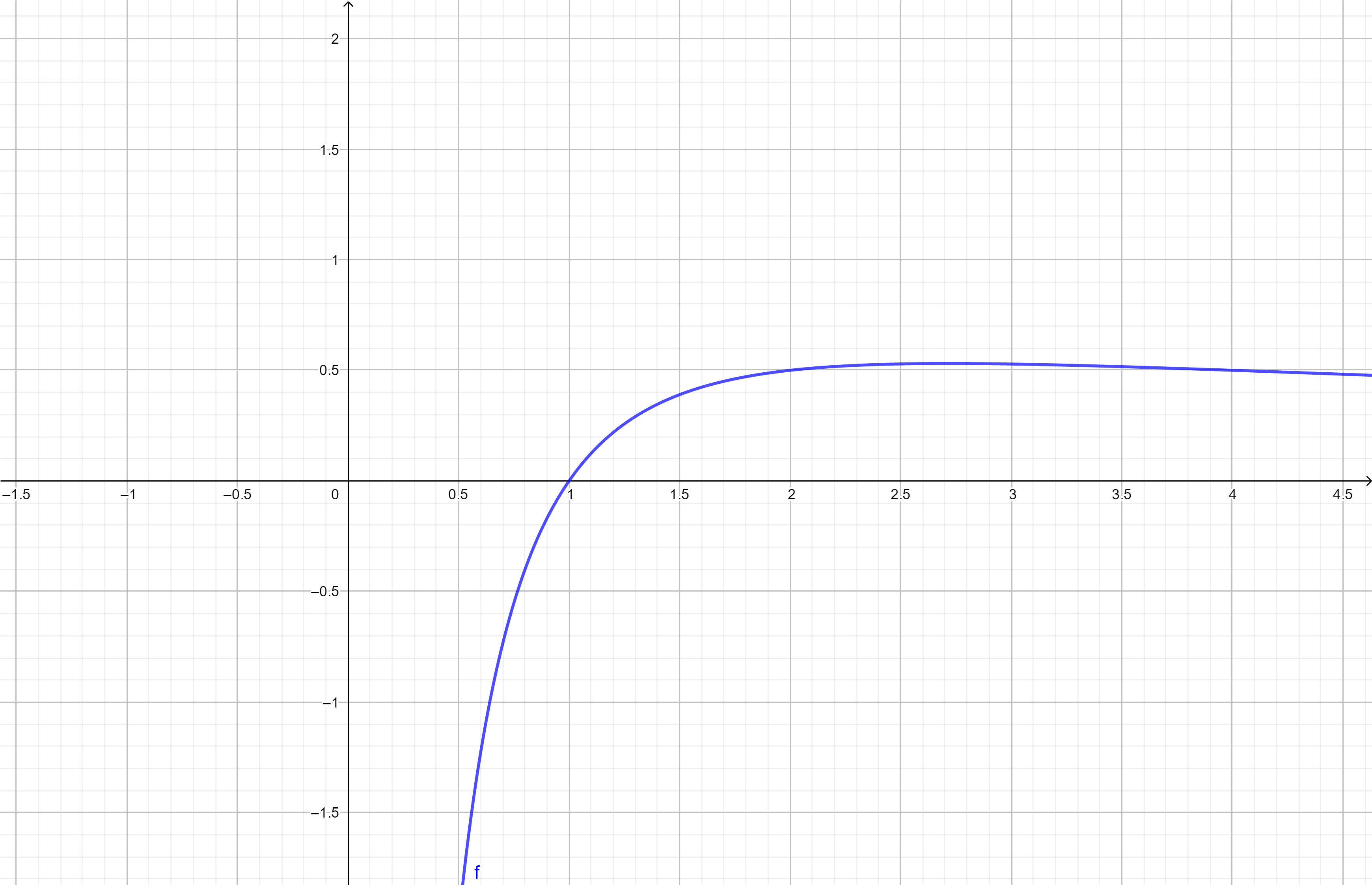
为什么无论底数是几,最高点的横坐标都是 $e$?
咱们来脑残证明一波:
首先,换底只会使图象沿 $y$ 轴成比例伸缩,不会改变最高点。因为假设把底数 $a$ 换成 $b$,那根据换底公式可得 $log_b{x} = log_a{x} imes log_b{a}$,$log_b{a}$ 是个与 $y$ 无关的常数,所以 $y=frac{log_a{x}}{x}$ 的图象只沿 $y$ 轴伸长 $log_b{a}$ 倍,最高点横坐标不变。
但是这个结论是封闭的,即我们需要找到一个 $x$,使得 $y=frac{log_a{x}}{x}$ 的图象最高点能通过其它方式求出来。
当 $x=e$ 时就可以证明这个图象的最高点的横坐标是 $e$,证明方法:
考虑求导,分数的导数公式为 $(frac{u}{v})' = frac{u'v-uv'}{v^2}$
令 $u=ln{x}$,$v=x$
$y=ln{x}$ 的导数为 $y'=frac{1}{x}$(至于这个核心公式怎么证,您们还是去查吧,这里篇幅不够且我能力有限),所以 $u'=frac{1}{x}$,$v'=1$。
推得 $(frac{ln{x}}{x})' = frac{1-ln{x}}{x^2}$
因为该函数只有最大值,没有最小值,所以图象上导数为 $0$ 的点就是最高点。
于是最高点的横坐标就是 $frac{1-ln{x}}{x^2} = 0$ 的解,容易解得 $x=e$。
至此我们证明了当 $x=e$ 时就可以证明这个图象的最高点的横坐标是 $e$,根据前文可知换底不会改变图象最高点,故无论底数 $a$ 为多少,$y=frac{log_a{x}}{x}$ 的图象最高点的横坐标都是 $e$。
综上,函数在 $[1,e]$ 区间递增,$[e,infty)$ 区间递减。
我们再求一下图象上与横坐标为 $2$ 的点的纵坐标相同的另一点,即求解 $2^x=x^2$。这个通过枚举就可以解得 $x=4$。所以图象在 $x=2$ 与 $x=4$ 处的纵坐标相同。
有了函数的分段变化情况,我们就可以判断 $frac{ln{x}}{x}$ 和 $frac{ln{y}}{y}$ 的大小关系了。
大力分类讨论即可。