树链剖分【模板】

参考博客

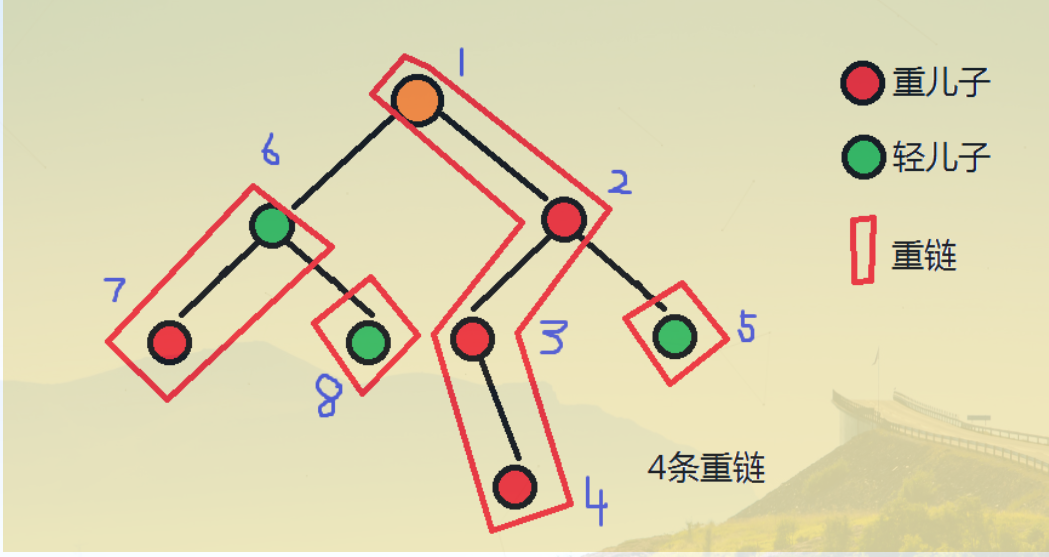
• 重儿子：对于每一个非叶子节点，它的儿子中 以那个儿子为根的子树节点数最大的儿子 为该节点的重儿子
• 轻儿子：对于每一个非叶子节点，它的儿子中 非重儿子 的剩下所有儿子即为轻儿子
• 叶子节点没有重儿子也没有轻儿子（因为它没有儿子。。）
• 重边：一个父亲连接他的重儿子的边称为重边 //原写法：连接任意两个重儿子的边叫做重边
• 轻边：剩下的即为轻边
• 重链：相邻重边连起来的 连接一条重儿子 的链叫重链
  • 对于叶子节点，若其为轻儿子，则有一条以自己为起点的长度为1的链
  • 每一条重链以轻儿子为起点

妙wa

博客上讲的挺详细的，也比较简单易懂

【树链剖分】

感觉挺妙的，其实树剖并不是很难，就是代码有些繁琐。

/*
 * @Author: zhl
 * @Date: 2020-10-13 20:36:59
 */
#include<bits/stdc++.h>
#define rep(i,a,b) for(int i = a;i <= b;i++)
#define repE(i,u) for(int i = head[u];i;i = E[i].next)
#define mid (l+r>>1)
#define lo (o<<1)
#define ro (o<<1|1)

using namespace std;
const int N = 4e5 + 10;
int A[N];
int n, m, root, mod;

struct Edge {
	int to, next;
}E[N << 1];

int head[N], tot;
void addEdge(int from, int to) {
	E[++tot] = Edge{ to,head[from] };
	head[from] = tot++;
}

int fa[N], sz[N], Tfa[N], dep[N], son[N];

//dfs1处理dep,sz,fa,son(重儿子)
void dfs1(int u, int p) {
	fa[u] = p;
	dep[u] = dep[p] + 1;
	sz[u] = 1;
	int mx = -1;
	repE(i, u) {
		int v = E[i].to;
		if (v == p)continue;
		dfs1(v, u);
		sz[u] += sz[v];
		if (sz[v] > mx)mx = sz[v], son[u] = v;
	}
}

int cnt;
int id[N], val[N], top[N];
//dfs2 剖分数链
void dfs2(int u, int topf) {
	id[u] = ++cnt;
	val[cnt] = A[u];
	top[u] = topf;
	if (!son[u])return;
	dfs2(son[u], topf);
	repE(i, u) {
		int v = E[i].to;
		if (v == fa[u] or v == son[u])continue;
		dfs2(v, v);
	}
}

int sum[N << 2], lz[N << 2];
int x, y, z;
void push_down(int o, int l, int r) {
	if (!lz[o])return;
	lz[lo] += lz[o];
	lz[ro] += lz[o];
	sum[lo] = (sum[lo] + lz[o] * (mid - l + 1)) % mod;
	sum[ro] = (sum[ro] + lz[o] * (r - mid)) % mod;
	lz[o] = 0;
}

void build(int o, int l, int r) {
	if (l == r) {
		sum[o] = val[l];
		return;
	}
	build(lo, l, mid);
	build(ro, mid + 1, r);
	sum[o] += sum[lo] + sum[ro];
}

void updt(int o, int l, int r) {
	if (x <= l and r <= y) {
		lz[o] = (lz[o] + z) % mod;
		sum[o] = (sum[o] + z * (r - l + 1)) % mod;
		return;
	}
	push_down(o, l, r);
	if (x <= mid)updt(lo, l, mid);
	if (y > mid)updt(ro, mid + 1, r);
	sum[o] = (sum[lo] + sum[ro]) % mod;
}

int query(int o, int l, int r) {
	if (x <= l and r <= y) {
		return sum[o];
	}
	int ans = 0;
	push_down(o, l, r);
	if (x <= mid)ans = (ans + query(lo, l, mid)) % mod;
	if (y > mid)ans = (ans + query(ro, mid + 1, r)) % mod;
	return ans;
}

int query_path(int a, int b) {
	int ans = 0;
	while (top[a] != top[b]) {
		if (dep[top[a]] < dep[top[b]])swap(a, b);
		x = id[top[a]]; y = id[a];
		ans = (ans + query(1, 1, cnt)) % mod;
		a = fa[top[a]];
	}
	if (dep[a] > dep[b])swap(a, b);
	x = id[a]; y = id[b];
	ans = (ans + query(1, 1, cnt)) % mod;
	return ans;
}
void updt_path(int a, int b, int k) {
	k %= mod;
	while (top[a] != top[b]) {
		if (dep[top[a]] < dep[top[b]])swap(a, b);
		x = id[top[a]]; y = id[a]; z = k;
		updt(1, 1, cnt);
		a = fa[top[a]];
	}
	if (dep[a] > dep[b])swap(a, b);
	x = id[a]; y = id[b]; z = k;
	updt(1, 1, cnt);
}

int main() {
	scanf("%d%d%d%d", &n, &m, &root, &mod);
	for (int i = 1; i <= n; i++)scanf("%d", A + i);

	for (int i = 1; i < n; i++) {
		scanf("%d%d", &x, &y);
		addEdge(x, y); addEdge(y, x);
	}
	dfs1(root, 0);
	dfs2(root, root);
	build(1, 1, cnt);
	while (m--) {
		int op; scanf("%d", &op);
		int a, b, c;
		if (op == 1) {//a,b 路径 + c
			scanf("%d%d%d", &a, &b, &c);
			updt_path(a, b, c);
		}
		if (op == 2) {//a,b 路径sum
			scanf("%d%d", &a, &b);
			printf("%d
", query_path(a, b));
		}
		if (op == 3) {//a的subtree + c
			scanf("%d%d", &a, &c);
			x = id[a]; y = id[a] + sz[a] - 1;
			z = c;
			updt(1, 1, cnt);
		}
		if (op == 4) {
			scanf("%d", &a);
			x = id[a]; y = id[a] + sz[a] - 1;
			printf("%d
", query(1, 1, cnt));
		}
	}
}

/*
5 50 2 24000
7 3 7 8 0
1 2
1 5
3 1
4 1
*/

我 debug 一晚上的罪魁祸首。

代码一刻钟，

debug两小时

bug 一字符