【leetcode】1292. Maximum Side Length of a Square with Sum Less than or Equal to Threshold

题目如下：

Given a m x n matrix mat and an integer threshold. Return the maximum side-length of a square with a sum less than or equal to threshold or return 0 if there is no such square. 

Example 1:

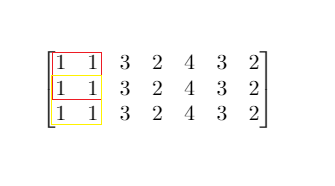
Input: mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
Output: 2
Explanation: The maximum side length of square with sum less than 4 is 2 as shown.

Example 2:

Input: mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
Output: 0

Example 3:

Input: mat = [[1,1,1,1],[1,0,0,0],[1,0,0,0],[1,0,0,0]], threshold = 6
Output: 3

Example 4:

Input: mat = [[18,70],[61,1],[25,85],[14,40],[11,96],[97,96],[63,45]], threshold = 40184
Output: 2 

Constraints:

• 1 <= m, n <= 300
• m == mat.length
• n == mat[i].length
• 0 <= mat[i][j] <= 10000
• 0 <= threshold <= 10^5

解题思路：记grid[i][j]为左上顶点坐标是(0,0)，右下顶点坐标为(i,j) 组成的矩形中每个坐标的和，grid很容易通过遍历一次mat求得。接下来就只要求mat中每个子矩形的和，如下图所示，要求绿色部分的矩形和，假设绿色矩形的右下顶点坐标是(i,j)只需要用grid[i][j] 减去两个黄色部分的矩形和，因为红色部分是两个黄色部分共有，因此做减法的时候多减了一次，需要再加回去，最终计算公式有：grid[i][j]  - 两个黄色子矩形和 + 红色子矩形和。

 代码如下：

class Solution(object):
    def maxSideLength(self, mat, threshold):
        """
        :type mat: List[List[int]]
        :type threshold: int
        :rtype: int
        """
        grid = [[0] * len(mat[0]) for _ in mat]
        for i in range(len(mat)):
            amount = 0
            for j in range(len(mat[i])):
                amount += mat[i][j]
                grid[i][j] = amount
                if i > 0:
                    grid[i][j] += grid[i-1][j]
        #print grid

        res = 0
        for i in range(len(grid)):
            for j in range(len(grid[i])):

                low,high = res,min(len(grid),len(grid[0]))
                while low <= high:
                    mid = (low + high)/2
                    if i + mid >= len(grid) or j + mid >= len(grid[0]):
                        high = mid - 1
                        continue
                    val = grid[i + mid][j + mid]
                    if j - 1 >= 0:
                        val -= grid[i + mid][j - 1]
                    if i - 1 >= 0:
                        val -= grid[i - 1][j + mid]
                    if i - 1 >= 0 and j - 1 >= 0:
                        val += grid[i - 1][j - 1]
                    if val <= threshold:
                        res = max(res, mid + 1)
                        low = mid + 1
                    else:
                        high = mid - 1

        return res