今天继续介绍——线段树之延迟标记
接上期《数据结构》线段树入门(一):http://www.cnblogs.com/shadowland/p/5870339.html
在上期介绍了线段树的最基本内容(线段树单点修改,区间查询),这次将介绍:区间修改,区间查询。
Question:
给你N个数,有两种操作:
1:给区间[a,b]的所有数增加X
2:询问区间[a,b]的数的和。
输入描述:
第一行一个正整数n,接下来n行n个整数,再接下来一个正整数Q,每行表示操作的个数,如果第一数是1,后接3个正整数,表示在区间[a,b]内每个数增加X,如果是2,表示操作2询问区间[a,b]的和是多少。
输入样例:
5
5 4 3 2 1
2
1 1 3 2
2 3 5
样例输出:
8
分析:
看到这个问题,我们能立刻想到,在主函数中添加一个循环,就像这样:
for ( int p=l ; p<=r ;++p )Update_Tree ( p , val , 1 );
进行r-l+1 次单点修改实现区间修改,但是仔细想想,对单个元素修改时间复杂度为O(Log2(n)), 所以对单个区间修改的复杂度为O(n*Log(n))——甚至比朴素的模拟算法还慢!
这里就将使用一种新方法:延迟标记(Lazy Tag)。
延迟标记就是在递归过程中,如果当前区间被需要修改的目标区间完全覆盖,那么就要停止递归,并且在上面做一个标记。但是这个信息没有更新到每个元素(即叶子节点),下次查询时可能无法得到足够的信息。我们不能忘了,之前在一个区间上打了一个标记,这个标记不仅仅是这个节点的性质,此性质作用于整个子树中。假设我们另一个查询中包含了当前区间的子孙区间,显然,这个标记也要对之后的查询产生影响。
仔细思考,第一期中元素的修改都是在叶节点中实现,不会对后续节点产生影响,类比这种想法,Lazy_Tag应运而生。如果如果当前区间被需要修改的目标区间完全覆盖,打一个标记。如果下一次的查询或更改包含此区间,那么将这个标记分解,并且传递给其左右儿子。
简单的说,延迟标记在我们需要时,才向下传递信息,如果没有用到,则不再进行操作。这个思想使处理的复杂度依然保持在O(log2(n))左右,相比朴素算法大大地降低了复杂度。
为了完成这种操作,我们可以在结构体中,增加一个add数组存储区间的延迟变化量。
举个例子:
这是一棵初始的线段树,其中,sum是我们维护的区间和,add是延迟修改量。add初值为0。

样例中有第一个操作:1 1 3 2 ,即在区间[1 , 3]加上2。
我们将3号节点add值加上2,sum值加上2*3,即2*区间长度,如图所示:
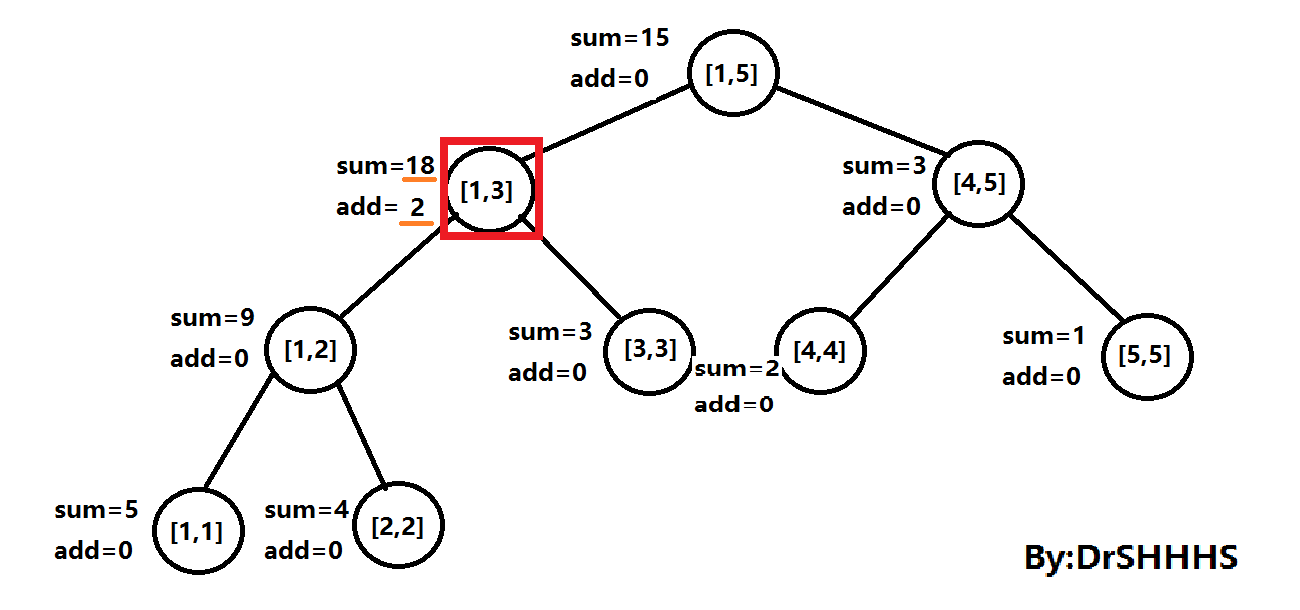
样例中第二个操作为 2 3 5 ,即查询区间[ 3 , 5 ]区间和。
在向下查找的过程中发现,路径上有一个add值不等于0的点,于是进行Push_Down操作(将区间分解并下传),如图所示。
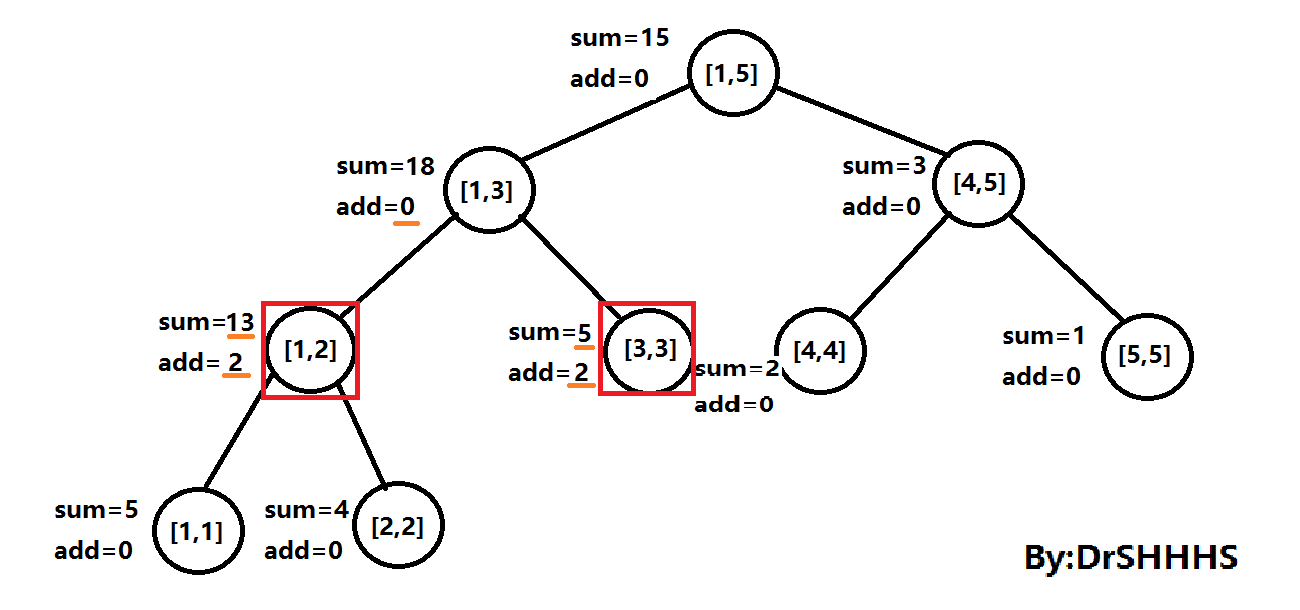
这时再返回[ 3 , 3 ]与[ 4 , 5 ]的值ans = 5 + 3 = 8;如图所示:

这时便完成了两次操作。
建议结合代码理解延迟标记,代码如下:
1 struct Tree 2 { 3 int l, r; 4 long long sum, add; 5 } tr[maxN << 2];
建树:
建树的过程同上期。
1 void Build_Tree ( int x , int y , int i) 2 { 3 tr[i].l = x ; 4 tr[i].r = y ; 5 if( x == y )tr[i].sum = arr[x]; 6 else 7 { 8 ll mid = ( tr[i].l + tr[i].r ) >> 1 ; 9 Build_Tree ( x , mid , i << 1); 10 Build_Tree (mid + 1 , y , i << 1 | 1 ); 11 tr[i].sum = tr[i << 1].sum + tr[i << 1 | 1].sum ; 12 } 13 }
标记下传:
1 void Push_down ( int i , int m )//i是当前结点编号,m = (tr[i].r - tr[i].l +1) 2 { 3 if(tr[i].add)//如果该节点有延迟标记 4 { 5 tr[i << 1].add += tr[i].add;//延迟标记给左儿子 6 tr[i << 1 | 1].add += tr[i].add;//延迟标记给右儿子 7 tr[i << 1].sum += tr[i].add * ( m - ( m >> 1 ) );//维护左儿子 8 tr[i << 1 | 1].sum += tr[i].add * ( m >> 1) ;//维护右儿子 9 tr[i].add = 0 ;//重要!!!,最后一定要清零!! 10 } 11 12 }
维护树:
1 void Update_Tree (int q , int w , int i) //[ q , w ]是目标区间,val是修改量 2 { 3 if( w >= tr[i].r && q <= tr[i].l) //当前区间被目标区间完全覆盖 4 { 5 tr[i].add += val; //延迟修改量+val 6 tr[i].sum += val * (tr[i].r - tr[i].l + 1); //加上维护区间总和=修改量*区间长度 7 return ; 8 } 9 else 10 { 11 Push_down( i , tr[i].r - tr[i].l + 1 ); //分解下传延迟信息 12 ll mid = (tr[i].l + tr[i].r ) >> 1; 13 if( q > mid ) 14 { 15 Update_Tree ( q , w , i << 1 | 1); //递归右区间 16 } 17 else if ( w <= mid ) 18 { 19 Update_Tree ( q , w , i << 1); //递归左区间 20 } 21 else //左右区间都有分布 22 { 23 Update_Tree ( q , w , i << 1 | 1); 24 Update_Tree ( q , w , i << 1); 25 } 26 tr[i].sum = tr[i << 1].sum + tr[i << 1 | 1].sum ; //回溯 27 } 28 }
查询树:
与单点修改区间查询基本类似。
1 long long Query_Tree (int q , int w , int i )//i当前结点,[ q ,w ]目标区间 2 { 3 if( w >= tr[i].r && q <= tr[i].l)//被目标区间完全覆盖,直接返回 4 { 5 return tr[i].sum; 6 } 7 else 8 { 9 Push_down( i , tr[i].r - tr[i].l + 1 );//查询也要下传延迟修改信息 10 long long mid = (tr[i].l + tr[i].r ) >> 1;//取中值 11 if( q > mid ) 12 { 13 return Query_Tree ( q , w , i << 1 | 1); 14 } 15 else if ( w <= mid ) 16 { 17 return Query_Tree ( q , w , i << 1); 18 } 19 else 20 { 21 return Query_Tree ( q , w , i << 1 | 1) + Query_Tree ( q , w , i << 1); 22 } 23 } 24 }
主程序:
1 int main ( ) 2 { 3 int N, M, op, l, r; 4 scanf("%d", &N); 5 for(int i = 1; i <= N; ++i)scanf("%d", &arr[i]) ; 6 Build_Tree ( 1 , N , 1 ); 7 scanf("%d", &M); 8 while (M--) 9 { 10 scanf("%d", &op); 11 if (op == 1) 12 { 13 scanf("%d%d%d", &l, &r, &val); 14 Update_Tree ( l , r , 1); 15 } 16 17 else 18 { 19 scanf("%d%d", &l, &r); 20 printf("%lld ", Query_Tree ( l , r , 1 )) ; 21 } 22 } 23 return 0 ; 24 }
其实上期的单点修改,区间查询只是 l==r 时的特例,单点查询Query_Tree ( l , l , 1 )同样可以完成单点查询。
PS:动态修改的RMQ问题(区间最值),也可以用带延迟标记的线段树完成。
(本期完)
To Be Continued ;