最大似然估计和最大后验估计（转）

本文主要介绍三类参数估计方法-最大似然估计MLE、最大后验概率估计MAP及贝叶斯估计。

 个人认为：三个参数估计的方法可以总结为如下：

我们知道贝叶斯公式是这样写的：

然后就可以通过这个公式来求解最大似然估计MLE、最大后验估计MAP和贝叶斯估计了。

最大似然估计：实际上是求了红线框起来的部分。认为参数是固定的

最大后验估计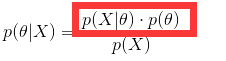：，实际上是去求了红线框起来的部分。比最大似然估计多了一个参数的概率，即我们认为参数也是有概率的。

贝叶斯估计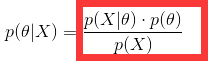：，求全部，此时不直接估计参数的值，而是允许参数服从一定概率分布。即也要求出p(x)来。

贝叶斯及贝叶斯派思考问题的固定模式

先验分布 + 样本信息  后验分布

上述思考模式意味着，新观察到的样本信息将修正人们以前对事物的认知。换言之，在得到新的样本信息之前，人们对的认知是先验分布，在得到新的样本信息后，人们对的认知为。

一. 频率学派与贝叶斯学派的区别

　　在查找“极大似然估计”有关知识点的时候，经常会碰到“频率学派”和“贝叶斯学派”这两个虽故事深厚，但是对于我们实际使用参数估计法并没有什么暖用的词，然而随着这两个词的曝光增多，它犹如一个没有解决的问题一样，潜伏在脑海深处，于是就在网上搜了一些结果，加工处理总结于此处。 
　　知乎上的回答[1]：

　　简单地说，频率学派与贝叶斯学派探讨「不确定性」这件事时的出发点与立足点不同。频率学派从「自然」角度出发，试图直接为「事件」本身建模，即事件A在独立重复试验中发生的频率趋于极限p，那么这个极限就是该事件的概率。举例而言，想要计算抛掷一枚硬币时正面朝上的概率，我们需要不断地抛掷硬币，当抛掷次数趋向无穷时正面朝上的频率即为正面朝上的概率。 
　　贝叶斯学派并不从试图刻画「事件」本身，而从「观察者」角度出发。贝叶斯学派并不试图说「事件本身是随机的」，或者「世界的本体带有某种随机性」，而只是从「观察者知识不完备」这一出发点开始，构造一套在贝叶斯概率论的框架下可以对不确定知识做出推断的方法。

　　豆瓣上的回答[２]：

　　这个区别说大也大，说小也小。往大里说，世界观就不同，频率派认为参数是客观存在，不会改变，虽然未知，但却是固定值；贝叶斯派则认为参数是随机值，因为没有观察到，那么和是一个随机数也没有什么区别，因此参数也可以有分布，个人认为这个和量子力学某些观点不谋而合。 
　　往小处说，频率派最常关心的是似然函数，而贝叶斯派最常关心的是后验分布。我们会发现，后验分布其实就是似然函数乘以先验分布再normalize一下使其积分到1。因此两者的很多方法都是相通的。贝叶斯派因为所有的参数都是随机变量，都有分布，因此可以使用一些基于采样的方法（如MCMC）使得我们更容易构建复杂模型。频率派的优点则是没有假设一个先验分布，因此更加客观，也更加无偏，在一些保守的领域（比如制药业、法律）比贝叶斯方法更受到信任。　

　　结合以上以及其他知乎上的回答，做一个总结，频率学派认为事物本身冥冥之中是服从一个分布的（至于是什么，只有上帝知道），这个分布的参数是固定的，因此，反过来想，上帝用这个分布制造了一些数据给了频率学派，频率学派的出发点是上帝在制造这些数据的时候那个参数是唯一固定的，我们要做的就是考虑哪个值最有可能是那个参数值呢，于是就有了“最大似然”和“置信区间”这样的概念，从名字就可以看出来他们关心的就是我有多大把握去圈出那个唯一的真实参数。然而贝叶斯学派认为，我们并没有上帝视角，怎么能够确定这些数据是用哪个固定参数值造出来的，因此他们关心的是参数空间的每一个值，给这些值一些他们自己认为合理的假设值（先验分布），然后在去做实验（证据），不断地调整自己的假设，从而得到最后结果（后验分布），但是又反过来想，既然我们不是上帝，那么这个先验假设又怎么能做出来了呢。 
　　频率学派太过于看中事实（太现实了），以至于容易被现实欺骗，比如掷硬币，掷了无数次都是正面，从频率学派的角度就会认为正面出现的概率为1；贝叶斯学派太过于幻想，以至于想象中的很多东西很难实现，例如很难准确判断参数的先验分布。总之，你我都不是上帝，所以也就没有绝对的孰对孰错。

有一点需要说明的，条件概率并不能说成是贝叶斯学派的，它只有结合先验概率并以求后验概率为目的的时候才能说成是贝叶斯的观点。

二. 频率学派的参数估计

1.极大似然估计

　　极大似然估计（Maximum Likelihood Estimate，MLE），也叫最 大似然估计，经过上述分析我们知道它是频率学派的思想，也就是为了求自认为的上帝的固定参数的，而尽量使这个参数接近真实。 
　　这里直接贴出[3]中的内容：

1) 离散随机变量的似然函数：

　　若总体X属离散型,其分布律P{X=x}=p(x;θ),θ∈Θ的形式为已知,θ为待估参数,Θ是θ可能的取值范围,设X1,X2,⋯,Xn是来自X的样本，则X1,X2,⋯,Xn的联合概率分布为

∏i=1np(x;θ)

　　设x1,x2,⋯,xn相应的样本值,易知样本X1,X2,⋯,Xn取到观察值x1,x2,⋯,xn的概率,亦即事件{X1=x1,X2=x2,⋯,Xn=xn}发生的概率为

L(θ)=L(x1,x2,⋯,xn;θ)=∏i=1np(x;θ)

　　这一概率随θ的取值而变化,它是θ的函数,L(θ)称为样本的似然函数(注意这里x1,x2,⋯,xn都是已知的样本值,它们都是常数) 
　　在θ可取的范围内挑选使似然函数L(x1,x2,⋯,xn;θ) 达到最大的参数值θ^ ,作为参数θ的估计值.即取θ^使:

L(x1,x2,⋯,xn;θ^)=argmaxθ∈ΘL(x1,x2,⋯,xn;θ)

2) 连续随机变量的似然函数：

　　若总体X属连续型,其概率密度f(x;θ),θ∈Θ的形式为已知,θ为待估参数,Θ是θ可能的取值范围,设X1,X2,⋯,Xn是来自X的样本，则X1,X2,⋯,Xn的联合概率密度为

∏i=1nf(x;θ)

　　设x1,x2,⋯,xn相应的样本值,则随机点X1,X2,⋯,Xn落在点x1,x2,⋯,xn的邻域(边长分别为dx1,dx2,⋯,dxn的n维立方体)内的概率近似为

∏i=1nf(x;θ)dxi

　　其值随θ的取值而变化,与离散的情况一样，取θ的估计值θ^使概率取到最大值,但因子∏ni=1dxi不随θ而变,故只需考虑函数

L(x1,x2,⋯,xn;θ^)=∏i=1nf(xi;θ)

的最大值，这里L(θ)就是样本的似然函数。

3) 最大似然估计一般求解过程：

　　(1) 写出似然函数； 
　　(2) 对似然函数取对数，并整理； 
　　(3) 求导数 ； 
　　(4) 解似然方程.

三. 贝叶斯学派的参数估计

1. 最大后验估计

　　最大后验估计（maximum a posteriori estimation，MAP），它与极大似然估计最大的区别就是，它考虑了参数本身的分布，也就是先验分布。 
　　这里直接贴出[4]中的内容 
　　最大后验估计是根据经验数据获得对难以观察的量的点估计。与最大似然估计类似，但是最大的不同时，最大后验估计的融入了要估计量的先验分布在其中（从第一节分析中我们可以得知这个先验分布可以理解为人们对事物的认识，也就是观察者的知识能力,先验分布的参数我们称为超参数(hyperparameter)）,故最大后验估计可以看做规则化的最大似然估计。 
　　假设x为独立同分布的采样，θ为模型参数,p为我们所使用的模型。那么最大似然估计可以表示为：

θ^MLE(x)=argmaxθp(x|θ)

　　现在，假设θ的先验分布为g。通过贝叶斯理论，对于θ的后验分布如下式所示：

p(θ|x)=p(x|θ)g(θ)∫θ∈Θp(x|θ′)g(θ′)dθ′

　　分母为x的边缘概率与θ无关，因此最大后验等价于使分子最大,故目标函数为：

θ^MAP(x)=argmaxθp(x|θ)g(θ)

2. 贝叶斯估计

　　请参考“Bayes估计”　 

参考：https://www.zhihu.com/question/20587681

其中，先验信息一般来源于经验跟历史资料。比如林丹跟某选手对决，解说一般会根据林丹历次比赛的成绩对此次比赛的胜负做个大致的判断。再比如，某工厂每天都要对产品进行质检，以评估产品的不合格率θ，经过一段时间后便会积累大量的历史资料，这些历史资料便是先验知识，有了这些先验知识，便在决定对一个产品是否需要每天质检时便有了依据，如果以往的历史资料显示，某产品的不合格率只有0.01%，便可视为信得过产品或免检产品，只每月抽检一两次，从而省去大量的人力物力。

而后验分布一般也认为是在给定样本的情况下的条件分布，而使达到最大的值称为最大后验估计。

1、最大似然估计MLE

首先回顾一下贝叶斯公式

这个公式也称为逆概率公式，可以将后验概率转化为基于似然函数和先验概率的计算表达式，即

最大似然估计就是要用似然函数取到最大值时的参数值作为估计值，似然函数可以写做

由于有连乘运算，通常对似然函数取对数计算简便，即对数似然函数。最大似然估计问题可以写成

这是一个关于的函数，求解这个优化问题通常对求导，得到导数为0的极值点。该函数取得最大值是对应的的取值就是我们估计的模型参数。

以扔硬币的伯努利实验为例子，N次实验的结果服从二项分布，参数为P，即每次实验事件发生的概率，不妨设为是得到正面的概率。为了估计P，采用最大似然估计，似然函数可以写作

其中表示实验结果为i的次数。下面求似然函数的极值点，有

得到参数p的最大似然估计值为

可以看出二项分布中每次事件发的概率p就等于做N次独立重复随机试验中事件发生的概率。

如果我们做20次实验，出现正面12次，反面8次

那么根据最大似然估计得到参数值p为12/20 = 0.6。

2、最大后验估计MAP

最大后验估计与最大似然估计相似，不同点在于估计的函数中允许加入一个先验，也就是说此时不是要求似然函数最大，而是要求由贝叶斯公式计算出的整个后验概率最大，即

注意这里P（X）与参数无关，因此等价于要使分子最大。与最大似然估计相比，现在需要多加上一个先验分布概率的对数。在实际应用中，这个先验可以用来描述人们已经知道或者接受的普遍规律。例如在扔硬币的试验中，每次抛出正面发生的概率应该服从一个概率分布，这个概率在0.5处取得最大值，这个分布就是先验分布。先验分布的参数我们称为超参数(hyperparameter)即

同样的道理，当上述后验概率取得最大值时，我们就得到根据MAP估计出的参数值。给定观测到的样本数据，一个新的值发生的概率是

下面我们仍然以扔硬币的例子来说明，我们期望先验概率分布在0.5处取得最大值，我们可以选用Beta分布即

其中Beta函数展开是

当x为正整数时

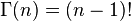
Beta分布的随机变量范围是[0,1],所以可以生成normalised probability values。下图给出了不同参数情况下的Beta分布的概率密度函数

我们取,这样先验分布在0.5处取得最大值，现在我们来求解MAP估计函数的极值点，同样对p求导数我们有

得到参数p的的最大后验估计值为

和最大似然估计的结果对比可以发现结果中多了这样的pseudo-counts,这就是先验在起作用。并且超参数越大，为了改变先验分布传递的belief所需要的观察值就越多，此时对应的Beta函数越聚集，紧缩在其最大值两侧。

如果我们做20次实验，出现正面12次，反面8次，那么

那么根据MAP估计出来的参数p为16/28 = 0.571,小于最大似然估计得到的值0.6，这也显示了“硬币一般是两面均匀的”这一先验对参数估计的影响。

3 贝叶斯估计

贝叶斯估计是在MAP上做进一步拓展，此时不直接估计参数的值，而是允许参数服从一定概率分布。回顾一下贝叶斯公式

现在不是要求后验概率最大，这样就需要求,即观察到的evidence的概率，由全概率公式展开可得

当新的数据被观察到时，后验概率可以自动随之调整。但是通常这个全概率的求法是贝叶斯估计比较有技巧性的地方。

那么如何用贝叶斯估计来做预测呢？如果我们想求一个新值的概率，可以由

来计算。注意此时第二项因子在上的积分不再等于1，这就是和MLE及MAP很大的不同点。

我们仍然以扔硬币的伯努利实验为例来说明。和MAP中一样，我们假设先验分布为Beta分布，但是构造贝叶斯估计时，不是要求用后验最大时的参数来近似作为参数值，而是求满足Beta分布的参数p的期望，有

注意这里用到了公式

当T为二维的情形可以对Beta分布来应用；T为多维的情形可以对狄利克雷分布应用

根据结果可以知道，根据贝叶斯估计，参数p服从一个新的Beta分布。回忆一下，我们为p选取的先验分布是Beta分布，然后以p为参数的二项分布用贝叶斯估计得到的后验概率仍然服从Beta分布，由此我们说二项分布和Beta分布是共轭分布。在概率语言模型中，通常选取共轭分布作为先验，可以带来计算上的方便性。最典型的就是LDA中每个文档中词的Topic分布服从Multinomial分布，其先验选取共轭分布即Dirichlet分布；每个Topic下词的分布服从Multinomial分布，其先验也同样选取共轭分布即Dirichlet分布。

根据Beta分布的期望和方差计算公式，我们有

可以看出此时估计的p的期望和MLE ，MAP中得到的估计值都不同，此时如果仍然是做20次实验，12次正面，8次反面，那么我们根据贝叶斯估计得到的p满足参数为12+5和8+5的Beta分布，其均值和方差分别是17/30=0.567, 17*13/(31*30^2)=0.0079。可以看到此时求出的p的期望比MLE和MAP得到的估计值都小，更加接近0.5。

综上所述我们可以可视化MLE,MAP和贝叶斯估计对参数的估计结果如下

个人理解是，从MLE到MAP再到贝叶斯估计，对参数的表示越来越精确，得到的参数估计结果也越来越接近0.5这个先验概率，越来越能够反映基于样本的真实参数情况。

原文地址：http://blog.csdn.net/yangliuy/article/details/8296481

参考文献

Gregor Heinrich, Parameter estimation for test analysis, technical report 

Wikipedia Beta分布词条 ,  http://en.wikipedia.org/wiki/Beta_distribution