题目链接:http://codeforces.com/contest/550
A、题意:给你一个串,问你这个串是否同时含有不相交的子串AB、BA
解:如果用类似dp的做法扫一遍就可以了。
也可以扫两遍:1、先找到一个AB,再在它后面找一个BA 2、先找到一个BA,在它后面找一个AB
代码用的是扫两遍的方法

1 /* 2 * Problem: 3 * Author: SHJWUDP 4 * Created Time: 2015/6/23 星期二 15:43:26 5 * File Name: 233.cpp 6 * State: 7 * Memo: 8 */ 9 #include <iostream> 10 #include <cstdio> 11 #include <cstring> 12 #include <algorithm> 13 14 using namespace std; 15 16 const int MaxA=1e5+7; 17 18 string str; 19 int main() { 20 #ifndef ONLINE_JUDGE 21 freopen("in", "r", stdin); 22 //freopen("out", "w", stdout); 23 #endif 24 while(cin>>str) { 25 int len=str.length(); 26 int pos=str.find("AB"); 27 if(pos!=string::npos && pos+2<=len && str.find("BA", pos+2)!=string::npos) { 28 puts("YES"); continue; 29 } 30 pos=str.find("BA"); 31 if(pos!=string::npos && pos+2<=len && str.find("AB", pos+2)!=string::npos) { 32 puts("YES"); continue; 33 } 34 puts("NO"); 35 } 36 return 0; 37 }
B、题意:给你一个有n道题的题库,每道题给出其难度,现在要你出题,要求是所有题目的难度总分数应当在[l, r]区间内,且最难的题与最简单题的难度差应大于等于x,问你总共有多少种出题方法
解:由于n很小,枚举所有出题方式即可

1 /* 2 * Problem: 3 * Author: SHJWUDP 4 * Created Time: 2015/6/23 星期二 16:20:37 5 * File Name: 233.cpp 6 * State: 7 * Memo: 8 */ 9 #include <iostream> 10 #include <cstdio> 11 #include <cstring> 12 #include <algorithm> 13 14 using namespace std; 15 16 const int INF=0x7f7f7f7f; 17 const int MaxA=15+7; 18 19 int N, L, R, X; 20 int arr[MaxA]; 21 int main() { 22 #ifndef ONLINE_JUDGE 23 freopen("in", "r", stdin); 24 //freopen("out", "w", stdout); 25 #endif 26 while(~scanf("%d%d%d%d", &N, &L, &R, &X)) { 27 for(int i=0; i<N; i++) { 28 scanf("%d", &arr[i]); 29 } 30 int lim=1<<N; 31 int ans=0; 32 for(int sta=0; sta<lim; sta++) { 33 int mx=-INF, mi=INF; 34 int sum=0; 35 for(int k=0; k<15; k++) { 36 if(sta&(1<<k)) { 37 mx=max(mx, arr[k]); 38 mi=min(mi, arr[k]); 39 sum+=arr[k]; 40 } 41 } 42 if(mx-mi>=X && L<=sum && sum<=R) { 43 ans++; 44 } 45 } 46 printf("%d ", ans); 47 } 48 return 0; 49 }
C、题意:给你一个长度最长为100位的十进制数,你可以去掉其中几位(或不去)使得这个数能被8整除
解:据说只要一个十进制数的后三位能被8整除,那么这个数能被8整除,那么我们就有了一个O(n^3)的算法
我是从后往前dp,用f[i][j]表示状态:到i位置模8余数为j,这样复杂度是O(8*n)

1 /* 2 * Problem: 3 * Author: SHJWUDP 4 * Created Time: 2015/6/23 星期二 16:20:37 5 * File Name: 233.cpp 6 * State: 7 * Memo: 8 */ 9 #include <iostream> 10 #include <cstdio> 11 #include <cstring> 12 #include <algorithm> 13 14 using namespace std; 15 16 const int INF=0x7f7f7f7f; 17 const int MaxA=100+7; 18 19 char str[MaxA]; 20 int arr[MaxA]; 21 int len; 22 int f[MaxA][8]; 23 bool vis[MaxA]; 24 int dfs(int u, int x, int base) {///base:10^t 25 if(x==0) return 1;///整除8 26 else if(u==-1) return 0; 27 else { 28 int& res=f[u][x]; 29 if(res!=-1) return res; 30 for(int i=u; i>=0; i--) { 31 int tmp=(x+base*arr[i])%8; 32 vis[i]=1; 33 if(dfs(i-1, tmp, base*10%8)) return res=1; 34 vis[i]=0; 35 } 36 return res=0; 37 } 38 } 39 int main() { 40 #ifndef ONLINE_JUDGE 41 freopen("in", "r", stdin); 42 //freopen("out", "w", stdout); 43 #endif 44 while(~scanf("%s", str)) { 45 len=strlen(str); 46 for(int i=0; i<len; i++) arr[i]=str[i]-'0'; 47 memset(f, -1, sizeof(f)); 48 memset(vis, 0, sizeof(vis)); 49 bool ok=0; 50 for(int i=len-1; i>=0; i--) { 51 int tmp=arr[i]%8; 52 vis[i]=1; 53 if(dfs(i-1, tmp, 10%8)) { 54 ok=1; 55 break; 56 } 57 vis[i]=0; 58 } 59 if(ok) { 60 puts("YES"); 61 for(int i=0; i<len; i++) { 62 if(vis[i]) printf("%d", arr[i]); 63 } 64 printf(" "); 65 } else puts("NO"); 66 } 67 return 0; 68 }
D、题意:给你一个k,问你k-regular图是否可以有桥,如果可以输出有桥的k-regular图(k-regular图:无向图,图上所有的点的度数均为k 桥:无向图上的一条边,去掉这条边,无向图会分成两块连通图)
解:我不知道怎么证明只知道有这么一种方法:
k为偶数时一定不行
先取一个点A作为桥上的一点,用k-1个点链接这个点,这k-1个点称为集合setA,现在用另外k-1个点setB中的每一个点与setA中的点相连,注意现在A和setA中点都已经满足k度,我们把setB中k-1个点两两相连,则它们也都满足k度

1 /* 2 * Problem: 3 * Author: SHJWUDP 4 * Created Time: 2015/6/23 星期二 17:13:43 5 * File Name: 233.cpp 6 * State: 7 * Memo: 8 */ 9 #include <iostream> 10 #include <cstdio> 11 #include <cstring> 12 #include <algorithm> 13 14 using namespace std; 15 16 int K; 17 int main() { 18 #ifndef ONLINE_JUDGE 19 freopen("in", "r", stdin); 20 //freopen("out", "w", stdout); 21 #endif 22 while(~scanf("%d", &K)) { 23 if(K%2==0) { 24 puts("NO"); continue; 25 } 26 puts("YES"); 27 printf("%d %d ", 4*K-2, 1+2*K*(K-1)+K-1); 28 int base=3; 29 printf("1 2 "); 30 for(int i=0; i<K-1; i++) { 31 printf("1 %d ", base+i); 32 for(int j=0; j<K-1; j++) { 33 printf("%d %d ", base+i, base+K-1+j); 34 } 35 } 36 for(int i=0; i<K-1; i+=2) { 37 printf("%d %d ", base+K-1+i, base+K-1+i+1); 38 } 39 base+=2*(K-1); 40 for(int i=0; i<K-1; i++) { 41 printf("2 %d ", base+i); 42 for(int j=0; j<K-1; j++) { 43 printf("%d %d ", base+i, base+K-1+j); 44 } 45 } 46 for(int i=0; i<K-1; i+=2) { 47 printf("%d %d ", base+K-1+i, base+K-1+i+1); 48 } 49 } 50 return 0; 51 }
E、题意:给你n个bool型值,你只能执行Implication和加括号两种操作,问你能不能得到false(Implication:
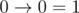

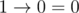
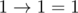
)
解:这个题感觉比D简单多了,有上面4个式子可以知道这些bool型值的最后一个一定是0,前面只要凑出一个1就可以了,大概是化成1->(0->(x))->0这样

1 /* 2 * Problem: 3 * Author: SHJWUDP 4 * Created Time: 2015/6/23 星期二 22:16:32 5 * File Name: 233.cpp 6 * State: 7 * Memo: 8 */ 9 #include <iostream> 10 #include <cstdio> 11 #include <cstring> 12 #include <algorithm> 13 14 using namespace std; 15 16 const int MaxA=1e6+7; 17 18 int N; 19 int arr[MaxA]; 20 int main() { 21 #ifndef ONLINE_JUDGE 22 freopen("in", "r", stdin); 23 //freopen("out", "w", stdout); 24 #endif 25 while(~scanf("%d", &N)) { 26 for(int i=0; i<N; i++) { 27 scanf("%d", &arr[i]); 28 } 29 if(arr[N-1]!=0) { 30 puts("NO"); continue; 31 } 32 int st=0; 33 while(st<N && arr[st]==1) st++; 34 if(st==N-1) { 35 puts("YES"); 36 if(st!=0) { 37 printf("1"); 38 for(int i=1; i<st; i++) { 39 printf("->%d", arr[i]); 40 } 41 printf("->"); 42 } 43 puts("0"); 44 } else if(st==N-2) { 45 puts("NO"); 46 } else { 47 puts("YES"); 48 if(st!=0) { 49 printf("1"); 50 for(int i=1; i<st; i++) { 51 printf("->%d", arr[i]); 52 } 53 printf("->"); 54 } 55 printf("(0->(%d", arr[st+1]); 56 for(int i=st+2; i<N-1; i++) { 57 printf("->%d", arr[i]); 58 } 59 puts("))->0"); 60 } 61 } 62 return 0; 63 }
