整除分块
此文章适合晚上阅读,因为是晚上写的,公式编辑器都是用的黑夜模式,白天看可能体验会差一点。
首先什么叫做整除分块:整除+分块.就是形如这个样子的式子:
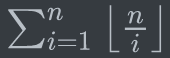
现在我们要求它的值,要求越快越好~
如果是实数除法可能就没法做了,但是这是整除啊,有很妙的性质呀,直接看一道例题吧。
余数之和:https://www.lydsy.com/JudgeOnline/problem.php?id=1257
题意概述:$n,k<=10^9$
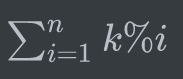
感觉这种题打表找规律是坠吼的。但是打完却没发现什么规律,只有一个小的优化,当$k<i$时,余数一定都是$k$。这样就把$n$变得最多和$k$一样大了,问题是$n,k$的范围是一样的,所以并没有什么用处...考虑展开:
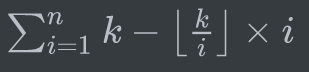
再展开一下:
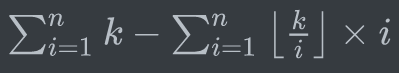
第一个和式可以$O(1)$算出来,关键是第二个。先不要管那个$*i$,把前面的除法打个表;
$k=10,n=10$

看起来好像有点规律?

相同的地方是可以一起算的,而且知道了块的任意一个元素就可以方便的知道结尾是什么,块的数量大约和$sqrt N$差不多,于是就做完了。

1 # include <cstdio> 2 # include <iostream> 3 4 using namespace std; 5 6 long long n,k,ans,ms; 7 8 int main() 9 { 10 cin>>n>>k; 11 if(n>k) ans+=(n-k)*k,n=k-1; 12 ans+=n*k; 13 int i=1; 14 while (i<=n) 15 { 16 ms=k/(k/i); 17 if(ms>n) ms=n; 18 ans-=(ms-i+1)*(i+ms)/2*(k/i); 19 i=ms+1; 20 } 21 printf("%lld",ans); 22 return 0; 23 }
当然整除分块能处理的问题远不止这些,否则就不会单独开一篇来写它了,下面还有一道难一点的整除分块题(不涉及任何其他算法):
模积和:https://www.lydsy.com/JudgeOnline/problem.php?id=2956
题意概述:$n,m<=10^9$
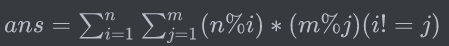
这题真是整除分块题....主要思路就是分块分块再分块。
现在来化一下式子,第二个和式中$n\%i$的值是一直不变的,可以提出来,但是因为$i!=j$的条件还要再容斥一下.
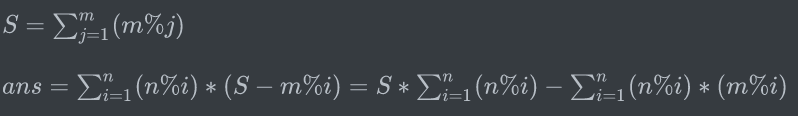
首先从简单的入手,先把$S$求出来,很显然的整除分块.现在求出$ans$的前半部分,对$n$进行分块后再乘上$S$即可.现在要求解的是$ans$的后半部分.
公式比较麻烦,所以下取整符号都没有打,这里面所有的分数格式都代表下取整.
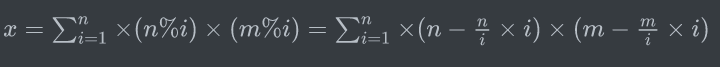
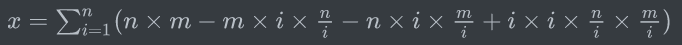

到了这里后,$x$的前三部分都可以运用整除分块求出来,而第四部分是一个很新奇的东西,以前没有见过.其实这里依旧很简单,因为$sqrt{N}$和$sqrt{M}$个块重叠在一起,即使每个分界线都不在同一点上最多会有$sqrt{N}+sqrt{M}$个块而已,在同一个块里$frac{n}{i}$和$frac{m}{i}$都是相同的,利用立方和公式求解即可.可以先写一个小程序把$2,6$的逆元求出来,就可以愉快的做模意义下的除法了.

1 # include <cstdio> 2 # include <iostream> 3 # define mod 19940417 4 # define ll long long 5 6 using namespace std; 7 8 ll n,m; 9 ll S=0,ans=0,x=0,inv2=9970209,inv6=3323403; 10 11 ll moo (ll n,ll m) //sum_{i=1}^n frac{m}{i}*i 12 { 13 ll ans=0; 14 ll x=1,l; 15 if(n>m) n=m; 16 while (x<=n) 17 { 18 l=min(m/(m/x),n); 19 ans=(ans+1LL*(l-x+1)*(x+l)%mod*inv2%mod*(m/x)%mod)%mod; 20 x=l+1; 21 } 22 return ans; 23 } 24 25 ll ipt() 26 { 27 ll ans=0; 28 ll mm,mn,l,x=1; 29 while (x<=n) 30 { 31 mm=m/x; 32 mn=n/x; 33 l=min(m/mm,min(n/mn,n)); 34 ans=(ans+mn*mm%mod*inv6%mod*(((l*(l+1)%mod*(2*l+1)%mod-(x-1)*x%mod*(2*x-1)%mod)%mod+mod)%mod)%mod)%mod; 35 x=l+1; 36 } 37 return ans; 38 } 39 40 int main() 41 { 42 scanf("%lld%lld",&n,&m); 43 if(n>m) swap(n,m); 44 S=((m*m%mod-moo(m,m))%mod+mod)%mod; 45 ans=((n*n%mod-moo(n,n))%mod+mod)%mod*S%mod; 46 x=n*n%mod*m%mod; 47 x=((x-m*moo(n,n))%mod+mod)%mod; 48 x=((x-n*moo(n,m))%mod+mod)%mod; 49 x=(x+ipt()); 50 ans=((ans-x)%mod+mod)%mod; 51 printf("%lld",ans); 52 return 0; 53 }
---shzr
