引言：当两类样本线性可分时，针对我们之前学习的感知机而言，存在多个超平面能将数据分开，这里要讨论什么样的分类面最好的问题。为此，我们形式化的定义了最优分类超平面，他有两点特征:1.能将训练样本没有错误的分开；2.在样本中距离超平面最近的样本与超平面之间的距离最大。
1.没有错误的分开：
对尺度影响的消除，可以将第一行式子中的0看成1e-6这种很小的数，而后下一个是式子则是对其进行放缩到1而得到的结果。
2.如果想要距离最大，首先要知道某一个样本点到分类面的距离表达式，（在线性判别函数那章讲过）
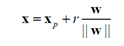
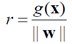
如果按照1.中所述，我们讨论的点中距离分类面最近的要落在|g(x)|=1上，那么
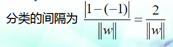
至此，我们得到了
一.线性可分支持向量机的数学表达形式：
求解上面这个优化问题：
1.将有约束优化问题通过拉格朗日乘子法转换为无约束的问题。（这里要讨论这个不等式约束与等式约束在向无约束问题进行转换时的异同，在PR&ML附录E（P708）中有详细讨论，过程略掉，结果是针对上述不等式约束问题，转换成了下面拉格朗日可变因子问题）
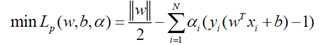
2.对 Lp中w,b令其一阶导数等于0，（注 ||w||的求导问题，有很多参考资料把目标函数写成||w||*||w||/2的形式了）
3.w,b带人Lp得得到其对偶形式Ld，及KKT条件，
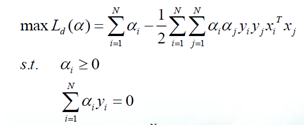
KKT条件:
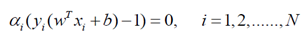
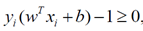
这里对alpha的求解可以看成是凸二次优化问题，理论讲解部分在《最优化理论方法》第九章中较为详细（没看懂），在matlab中有函数可以直接求解 ，把上面的函数对应到
中，然后使用 x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0)，进行求解即可。
4.得到alpha之后通过2.中的等式求解w
5.根据KKT条件中的第二个
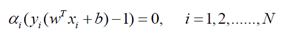
如果我们求解得到的alpha中，
，那么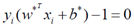
，这个时候的样本就是我们要找的支持向量。
二.线性支持向量机与软间隔最大化
同样要解其对偶问题
随之而来的问题就是如何选择C
