隐马尔可夫模型（二）

学习算法

训练数据集为观测序列，此外还可能有对应的状态序列（比如人工标注），如果包含了对应的状态序列则为监督学习，否则称非监督学习。

监督学习

设训练数据集包含S个长度相同的观测序列和对应的状态序列{(O₁,I₁), (O₂,I₂), ... , (O_s,I_s)}，那么可用极大似然估计法来估计隐马尔可夫模型的参数λ=(A,B,π)

注：这里暂不清楚为什么要观测序列长度相同，实际上不太可能做到观测序列的长度相同，当然，个人认为也没必要长度相同。

（1）转移概率的估计

设样本中从状态i转移到状态j的频数为A_ij（统计所有状态序列），那么状态转移概率的估计为

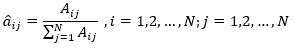  (1)

其中，右端分母表示从状态i转移到任何状态的频数总和，N表示所有可能的状态数

（2）观测概率的估计

b_i(m)表示处于状态i之下观测为m的条件概率，根据极大似然估计，则为样本中，处于状态i下观测为m的频数（B_im）与处于状态i下观测为任意值的频数之比，即

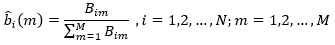  (2)

其中，M表示所有可能的观测数

（3）初始状态概率的估计

初始状态概率向量π维度为N，其中π_i为样本中状态i出现的频率，

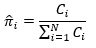                               (3)

其中C_i表示样本中状态 i 出现的频数

以上学习过程比较简单，不再赘述

非监督学习

Baum-Welch算法

设训练数据集仅包含S个长度为T的观测序列{O₁,O₂,...,O_s}，目标是学习隐马尔可夫模型的参数λ=(A,B,π)。

（注：这里为什么又是需要长度均为T？嗯...《统计学习方法》里面就是这样，我也没想明白，如果以后想明白了或者在其他地方看到关于这个的解释，再来这里补充吧。）

将观测序列数据看作观测数据O，状态序列数据看作不可观测的隐数据I，隐马尔可夫模型为一个含有隐变量的概率模型

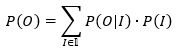        (4)

加上参数λ后的形式如下

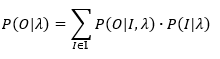  (5)

参数学习方法使用EM算法（如还不熟悉可以去这里温故知新一下）。观测数据O={o₁,o₂,...,o_T}，隐数据I={i₁,i₂,...,i_T}，完全形式数据为(O,I)=(o₁,o₂,...,o_T,i₁,i₂,...,i_T)，对数似然函数为logP(O,I|λ)

EM算法中Q函数为

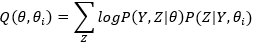
其中Y为观测数据，Z为隐变量数据，θ是参数，类比之下，我们可以写出隐马尔可夫模型的Q函数如下

   

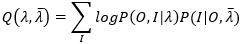
λ ̅ 是当前参数估计值，λ 是要极大化的隐马尔可夫模型参数。

观测序列与状态序列关于参数λ的联合概率分布为

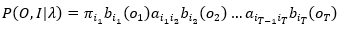            (7)

代入(6)式，并根据积的对数等于对数的和，得

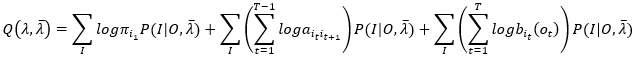 (8)

其中，T表示观测序列长度

 E步：计算(8)式得到Q(λ,λ ̅ )

 M步：极大化Q(λ,λ ̅ )求模型参数λ=(A,B,π)

由于三个参数分别在(8)式的三个子项中，所以对各项分别极小化

（1）第一项表示所有可能的状态序列求和，假设状态序列长度为T，所有可能的状态数量为N，则所有可能的状态序列的数量则为T^{^}N，第一项可以写成

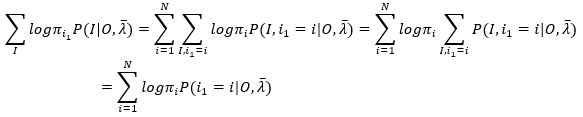    (9)

其中πi满足约束条件

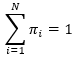                                                                                       (10)

注意(9)中的变换，(9)中第一个等号后的项表示两重求和，外层表示对第一个状态 i₁ 的所有可能状态求和，假设当前i₁=i，那么内层求和表示确定了第一个状态 i₁ 之后所有可能的状态序列的Sigma求和。

举个例子，状态序列为(i₁,i₂,i₃)，可能的状态为(a,b,c)三种，那么这个两重求和为

for i1 in [a,b,c]
    for i2,i3 in [(a,a),(a,b),(a,c),(b,a),(b,b),(b,c),(c,a),(c,b),(c,c)]
        ...
    end
end

再看第一个等号后的项，对内层求和，logπ_i 是常数，可以提到内层求和的外面，于是有(9)的第二个等号后的项，此时内层求和就表示 i₁=i的边缘概率分布，于是得到第三个等号后的项

(9)式利用拉格朗日乘子法，拉格朗日函数为

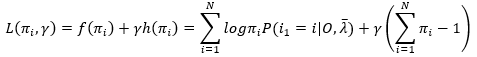       (11)

对π_i求偏导，令其等于0，得

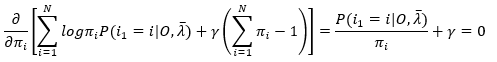   (12)

注意上式对任意的i，i=1,2,...,N均成立，求偏导时，求和符号可以去掉，因为在i为某一值时，π_i为自变量，而π_j(j!=i) 可以看作常数，所以，

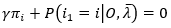                                                                   (13)

注意，上式对任意i, i=1,2,...,N均成立，所以对i求和，再根据(10)式和条件概率分布之和为1，有

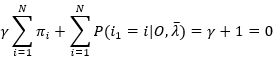      (14)

求得 γ = -1，代入(13)式，有

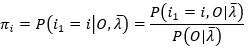           (15)

(15)式右端，分母表示在当前模型参数下，观测序列O出现的概率，这可以通过上一篇文章中关于概率问题的分析求得，分子表示在当前模型参数下，第一个状态为 i 时的观测序列出现的概率，显然这也是上一篇文章中分析的概率问题，分子分母满足如下关系，

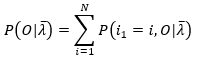                   (16)

（2）观察第二项，发现因子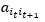，表示t时刻在i_t状态下转移到t+1时刻状态i_t+1的概率，所以对第二项的转换势必需要考虑状态对 state pair (i_t,i_t+1)的所有排列，令i_t=i, i_t+1=j，

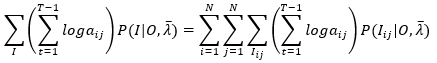            (17)

与上面的分析类似，将对I的所有排列的一重求和拆分成三重求和，最外层是对 i 的所有可能状态求和，次外层是对 j 的所有可能状态求和，第三层是已知 i 和 j 的情况下，对状态序列的所有排列(序列变量为I_ij)的求和，显然对第三层求和来说，上式中括号内的部分是常数，可以提到第三层的外面，即

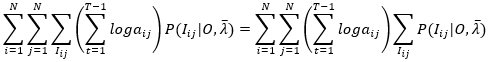  (18)

观察右端最右边的求和，可能我这里符号表示不是很清楚，看下面的等式就知道含义了

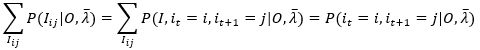    (19)

代入(18)式，得

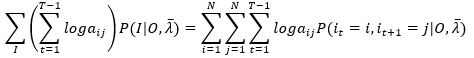     (20)

于是第二项的转换也完成

类似第一项的处理采用拉格朗日乘子法，注意到约束条件

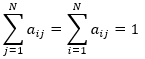      (21)

拉格朗日函数为

  (22)

对a_ij求偏导，令其等于0

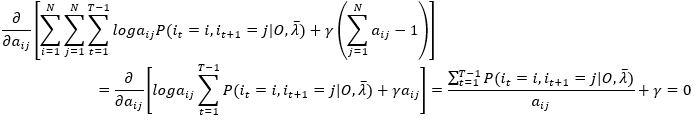 (23)

注意，上式的变换利用事实：对任意i=1,2,...N 和任意 j=1,2,...,N 均成立，a_ij为自变量，其他a_mn看作常数，于是

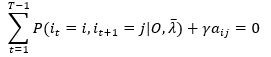        (24)

对 j 求和并利用 (21)的约束条件，有

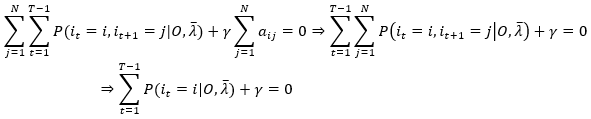
上式推导中，i_t和i_t+1看成是二维随机变量，其联合概率分布P(i_t=i,i_t+1=j)，对 j 的求和就得到i_t=i的边缘概率。于是

                     (25)

代入(24)式，得

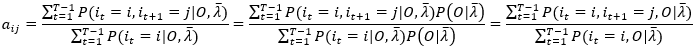
上式，由于条件概率不容易直接求得，所以分子分母同时乘以一个常数P(O|λ ̅)进行变换得到t时刻状态i和观测序列O的联合概率比较容易求得，所以

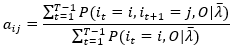                   (26)

 上式的计算可以通过上一篇文章中概率问题分析计算得到，比如分母表示给定模型参数λ ̅，出现观测序列O且t时刻状态为i的概率，可通过前向算法和后向算法得到。

 （3）有了前两项的转换分析，相信第三项的变换也不难了，这里不再赘述，直接给出推导过程

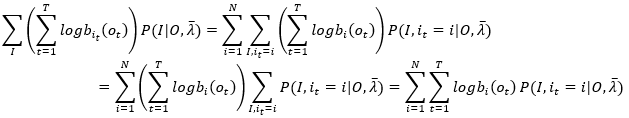  (27)

 约束条件为

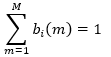                           (28)

其中，m=1,2,...,M，M为所有可能的观测值数量，约束条件的含义是处于状态 i 总是会出现一个观测值（概率为1）

类似地，利用拉格朗日乘子法，拉格朗日函数为

 

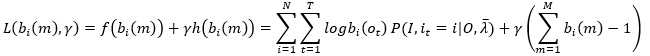
观察上式，发现t时刻观测值o_t不一定等于观测值v_m（m表示观测值在观测值列表中的下标），因为我们使用bi(m)作为自变量，所以当o_t!=v_m时，b_i(o_t)就成了自变量，否则可以看作常数，所以在对拉格朗日函数求b_i(m)的偏导时，引入指示函数(indicator function)：

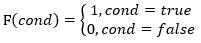
（见谅，这里函数名写成F而不是常见的I，是为了与状态序列I 区分）

于是

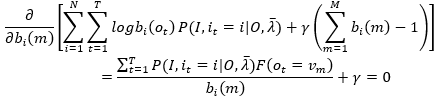
变换得，

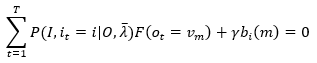        (29)

 根据(28)的约束条件，对上式m求和，m=1,2,...,M，得

 

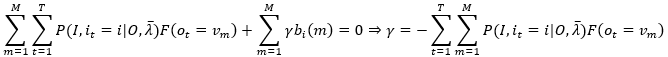
注意最右端内层求和，由于观测值列表中不可能有重复的值，所以只有一个观测值假设下表为k，即m=k时，o_t=v_m，指示函数F输出为1，其他情况F 输出为0，所以

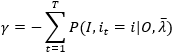
代入(29)式，得

          

由于分子分母为条件概率，乘以常数P(O|λ ̅)，变换为联合概率容易计算，所以

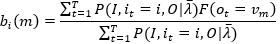       (30)

这样分子分母的计算就可以通过上一篇文章的概率问题分析计算得到。

总结

Baum-Welch模型参数估计公式：

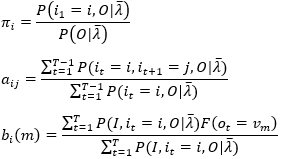     (31)

步骤

输入：观测数据O，长度为T

输出：隐马尔可夫模型参数

1. 初始化，选择λ=(A,B,π)的初值，初值的选择可以根据最大熵原理，即每个事件等可能出现，概率为均值。
2. 递推，对n=1,2,...，利用(31)公式组计算更新模型参数
3. 结束，得到最终模型参数λ=(A,B,π)

实际中，观测数据O肯定不止一组，比如非监督学习一开始设定的是S组，此时如何学习呢？

对于观测数据O不止一组的情况下，比如S组观测序列，这里我目前还没有去找资料求证过，也还没深入思考过，不过我认为可以如下计算：

1. 对这S组观测序列分别使用非监督学习计算各自的模型参数
2. 利用预测算法计算S组观测序列各自的状态序列（下一篇文章中讨论预测算法）
3. 利用监督学习方法计算得到一个总的模型参数

ref

统计学习方法，李航