Poj 1654--Area(叉积)

Area

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 17377		Accepted: 4827

Description

You are going to compute the area of a special kind of polygon. One vertex of the polygon is the origin of the orthogonal coordinate system. From this vertex, you may go step by step to the following vertexes of the polygon until back to the initial vertex. For each step you may go North, West, South or East with step length of 1 unit, or go Northwest, Northeast, Southwest or Southeast with step length of square root of 2. 

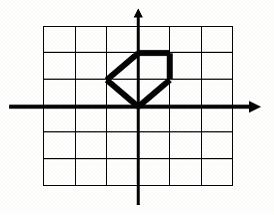
For example, this is a legal polygon to be computed and its area is 2.5: 

Input

The first line of input is an integer t (1 <= t <= 20), the number of the test polygons. Each of the following lines contains a string composed of digits 1-9 describing how the polygon is formed by walking from the origin. Here 8, 2, 6 and 4 represent North, South, East and West, while 9, 7, 3 and 1 denote Northeast, Northwest, Southeast and Southwest respectively. Number 5 only appears at the end of the sequence indicating the stop of walking. You may assume that the input polygon is valid which means that the endpoint is always the start point and the sides of the polygon are not cross to each other.Each line may contain up to 1000000 digits.

Output

For each polygon, print its area on a single line.

Sample Input

4
5
825
6725
6244865

Sample Output

0
0
0.5
2

Source

POJ Monthly--2004.05.15 Liu Rujia@POJ

 

叉积（二维坐标）：c(a, b);   d(e, f);   c X d = a*f - b*e;  智商问题  无限wrong.

#include <cstdio>
#include <cstring>
const int MAXN = 1000001;
char str[MAXN];
int ac[10][2]={0, 0, -1, -1, 0, -1, 1, -1, -1, 0, 0, 0, 1, 0, -1, 1, 0, 1, 1, 1};
int main(){
    int T;
    scanf("%d", &T);
    while(T--){
        scanf("%s", str);
        long long sum = 0;
        int a = ac[str[0]-'0'][0];
        int b = ac[str[0]-'0'][1];
        for(int i = 1; i < strlen(str); i++){
            int c = a + ac[str[i]-'0'][0];
            int d = b + ac[str[i]-'0'][1];
            sum += a*d - b*c;
            a = c; b = d;
        }
        if(sum < 0)
            sum = -sum;
        printf("%lld", sum/2);
        if(sum%2)
            printf(".5");
        printf("
");
    }
    return 0;
}