CV 之基于特征的配准（1）—— 2D 和 3D 特征的配准

首先引入几何配准和标定的例子：

基于特征的配准是从两个或者多个匹配的 2D 或 3D点的集合中估计运动的问
题。

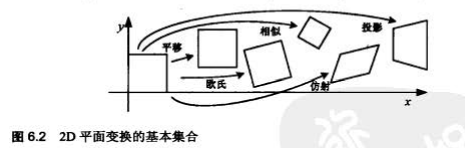
一、使用最小二乘的 20 配准

给定匹配的特征点集合(｛ X_i，x_{i}^{'}｝)和以下形式的平面参数变换：

[x^{'} = f left( x ; p ight) ]

为了最好地估计运动参数 ，常用的方法是最小二乘法，也就是最小化残差平方和。

对于不同的变换对应的矩阵和雅可比矩阵总结如下：

二、应用：全景图

图像配准一个最简单的应用是一种特殊形式的图像拼接，称为“全景图”．在全景图里，在用简单的平均进行融合之前，图像会被平移， 可能还有旋转和缩放。

例如下图：

旋转和缩放变换的公式：

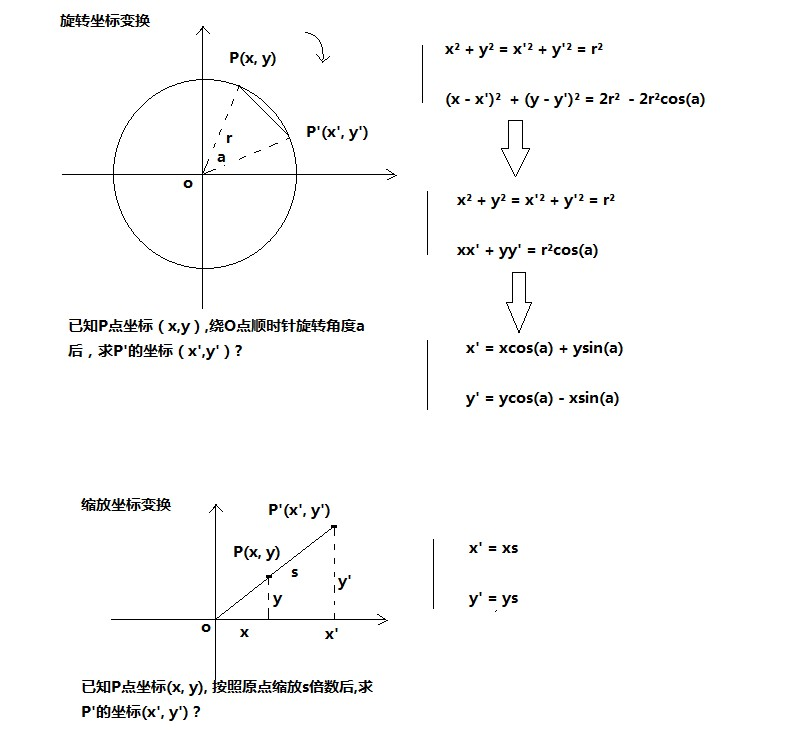
三、迭代算法

线性最小二乘是最简单的参数估计方法，然而在计算机视觉中大多数问题在测
量值和未知值之间不存在简单的线性关系．在这种情况下得到的问题称为“非线性最小二乘”（non-linear least squares）或者“非线性回归’（non-linnear regression).

四、鲁棒最小二乘和 RANSAC

常规的最小二乘对其中噪声符合正态（高斯）分布的量测来说是一个合适的选择。然而在对应点中有外点时，需要更鲁棒的最小二乘．在这种情况下，绿好用*** M-估计**（它对残差施加一个鲁棒惩罚函数 (p(r)) 来代替它们的平方。）

M-估计常常能够减少外点的影响，但是一些情况中，从太多外点起步会
使得 IRLS（或者其他梯度下降算法）不能收敛到全局最优。更好地方法是寻找一个岂不对应的内点集合，也就是与主动运动估计一致的点。主要有两种方法（均为先随机选择 k 个对应点子集，然后计算出事的估计 (p), 再计算对应点全集的残差）;

1. Random Sample Consensus
2. 最小中位方差

五、3D 配准

不同于 2D 图像特征配准，很多计算机视觉应用需要配准3D 点，在 3D变换对运动参数是线性的情况下，eg.平移、相似和仿射变换，可以使用常规的最小二乘法。

对于欧式运动的情况，被称为“绝对方向”问题，需要采用以下两种方法：

1. 正交 Procrustes 算法：通过计算 3×3 相关矩阵的 singular value decomposition（SVD）分解，得到旋转矩阵。
2. 绝对方向算法：估计对应与旋转矩阵 (R) 的单位四元组，找到具有最大正特征值的特征向量。

有实验将其他两种方法对比，证明以上两种方法的精度差可以忽略不计。