NOIP2017DAY1T3——逛公园

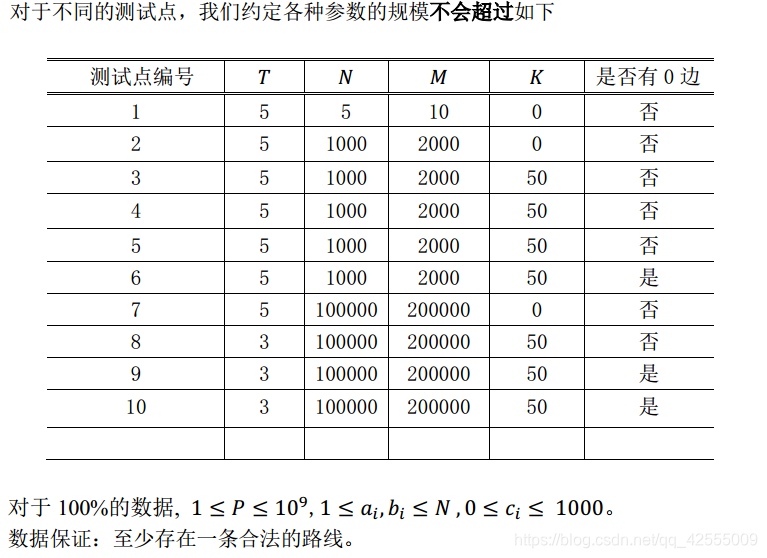
输入
第一行包含一个整数 T, 代表数据组数。
接下来T组数据，对于每组数据：
第一行包含四个整数 n, m, k, p， 每两个整数之间用一个空格隔开。 接下来m行，每行三个整数ai,bi, ci， 代表编号为ai, bi的点之间有一条权值为 ci的有 向边，每两个整数之间用一个空格隔开
输出
输出文件包含 T行，每行一个整数代表答案。
样例输入
2
5 7 2 10
1 2 1
2 4 0
4 5 2
2 3 2
3 4 1
3 5 2
1 5 3
2 2 0 10
1 2 0
2 1 0
样例输出
3
-1
提示
对于第一组数据，最短路为 3。 1 – 5, 1 – 2 – 4 – 5, 1 – 2 – 3 – 5 为 3 条合法路径。

肯定要先跑最短路嘛

然后我们可以发现k的范围很小

可以直接枚举k的大小

发现对于两个相连点$u$、$v$

u可以将其方案继承给v

所以考虑dp

$f[i][j]$表示到点$i$,比1到$i$的最短路长$j$的方案数

可以发现其实就是一个类完全背包的模型

所以直接从后往前搜就可以了

注意判0环的情况

我在网上搜到的好几篇都是这样记忆化搜索的

但是有些的写法是有一些问题的

比如直接给1赋dp的值

而dp的时候是直接遇到一个访问过的点就return点的值

但直接给1点赋dp初值会处理不了1在环里的情况

所以单独建了个虚点

只和1相连

给虚点赋dp初值

这样搜到1的时候就会继续搜下去

就不会出问题了

#include<bits/stdc++.h>
using namespace std;
#define mk make_pair
#define ll long long
inline int read(){
 char ch=getchar();
 int res=0,f=1;
 while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
 while(isdigit(ch))res=(res<<3)+(res<<1)+(ch^48),ch=getchar();
 return res*f;
}
const int M=200005;
const int N=100005;
int T,n,m,k,p,cnt,adj[N],nxt[M],len[M],to[M],in[N],val[M],dis[N],nec[M],head[N],go[M],tot;
bool vis[N][55],flag;
ll f[N][55],ans;
inline void clear(){
 memset(adj,0,sizeof(adj));
 memset(to,0,sizeof(to));
 memset(val,0,sizeof(val));
 memset(f,-1,sizeof(f));
 memset(nxt,0,sizeof(nxt));
 memset(vis,0,sizeof(vis));
 memset(nec,0,sizeof(nec));
 memset(len,0,sizeof(len));
 memset(go,0,sizeof(go));
 memset(head,0,sizeof(head));
 flag=cnt=ans=0;
}
inline void addedge(int u,int v,int w){
 nxt[++cnt]=adj[u],adj[u]=cnt,to[cnt]=v,val[cnt]=w;
 nec[cnt]=head[v],head[v]=cnt,go[cnt]=u,len[cnt]=w;
}
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >q;
inline void dijkstra(){
 memset(dis,127/3,sizeof(dis));
 dis[1]=0,q.push(mk(dis[1],1));
 while(!q.empty()){
  int u=q.top().second;q.pop();
  for(int e=adj[u];e;e=nxt[e]){
   int v=to[e];
   if(dis[u]+val[e]<dis[v]){
    dis[v]=dis[u]+val[e];
    q.push(mk(dis[v],v));
   }
  }
 }
}
inline int dfs(int u,int s){
 if(~f[u][s])return f[u][s];
 f[u][s]=0,vis[u][s]=1;
 for(int e=head[u];e;e=nec[e]){
  int v=go[e],pos=s+dis[u]-len[e]-dis[v];
  if(pos<0)continue;
   if(vis[v][pos])flag=1;
   f[u][s]+=dfs(v,pos),f[u][s]%=p;
 }
 vis[u][s]=0;
 return f[u][s];
}
int main(){
 T=read();
 while(T--){
  clear();
  n=read(),m=read(),k=read(),p=read();
  for(int i=1;i<=m;i++){
   int u=read(),v=read(),w=read();
   addedge(u,v,w);
  }
  dijkstra();
  addedge(n+1,1,0);
  f[n+1][0]=1;dis[n+1]=0;
  for(int i=0;i<=k;i++)ans+=dfs(n,i),ans%=p;
  if(flag)cout<<"-1"<<'
';
  else cout<<ans<<'
';
 }
}