Codeforces 1485C

Codeforces Round #701 (Div. 2) C. Floor and Mod

题意

给定(x,y)，询问当(1le ale x, 1le ble y)时，(lfloor frac a b floor=a mod b)的对数

限制

(1le x,yle 10^9)

思路

（想法有很多种，本文主要通过分块求解）

（并没有那么难，但为什么总是往难的方向想呢……）

读懂题意后如果用公式化简

根据(a mod b=a-lfloor frac a b floor*b)，最多只能够化到(a=(b+1)*lfloor frac a b floor)

可得(frac a {b+1}=lfloor frac a b floor)

明显，(b+1)一定是(a)的因子

（然后就想不到其他规律了）

---

那么我们枚举(b)，再枚举(b+1)的倍数进行打表

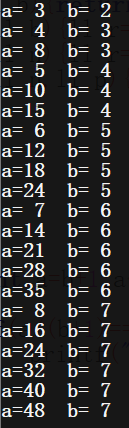
得到规律：

对于任意大于(2)的正整数(b)

满足题意的(a)最多有(b-1)项，每一项都是(b+1)的倍数，最大项为((b-1)*(b+1))

---

所以对于每个(b)，我们可以先求出(1)到(x)内有多少(b+1)的倍数（即(lfloorfrac x {b+1} floor)个）

在计算答案时，根据规律需要将其与(b-1)取小

但是这种方法的时间复杂度为(O(y=10^9))，不可行

考虑优化，发现如果((b-1)*(b+1)gt x)，即(lfloorfrac x {b+1} floor lt b-1)时

受(x)的限制，会有一段段连续的(b)对应的答案数量相同，且答案均为(lfloorfrac x {b+1} floor)

直接考虑分块，令(t=lfloorfrac x {b+1} floor)表示当前段的答案，再通过(lfloorfrac x t floor)来求出满足答案为(t)的最大的(b+1)的值

故此时最大的(b)应为(lfloorfrac x t floor-1)，注意与(y)取小即可

该段的答案即段长度*t，其后让(b)直接成为右端点(+1)即可

当((b-1)*(b+1)le x)时，对于每个(b)的答案数量均为(b-1)

故我们可以求出满足((b-1)*(b+1)le x)以及(ble y)的最大的(b)

那么答案就是(1+2+3+cdots +(b-1))，直接等差求和公式即可

对于这个最大的满足((b-1)*(b+1)le x)的(b)，先忽略条件(ble y)，结论是(maxb=lfloorsqrt x floor)或(maxb=lfloorsqrt x floor +1)

或者这里也可以打表找规律

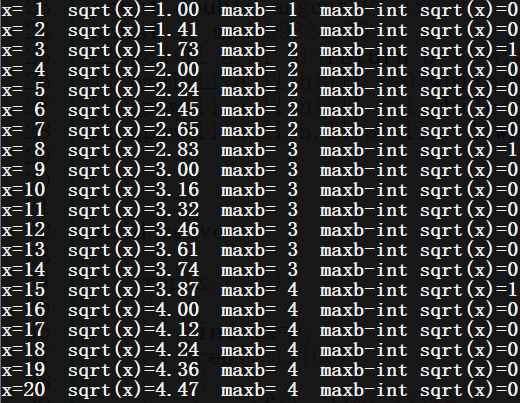
对于(maxb+1)到(y)，还是分块处理

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

void solve()
{
    int x,y;
    scanf("%d%d",&x,&y);
    
    int b=sqrt(x)+1;
    if(1LL*(b-1)*(b+1)>x)
        b--;
    b=min(b,y); //注意与y取小
    ll ans=1LL*b*(b-1)/2;
    
    for(b++;b<=y;)
    {
        int t=x/(b+1);
        if(t==0)
            break;
        
        int nxt=min(x/t-1,y); // 注意x/t是对于b+1的最大值
        ans+=1LL*(nxt-b+1)*t;
        
        b=nxt+1;
    }
    printf("%lld
",ans);
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
        solve();
    return 0;
}