数据结构：两栈共享空间

两栈共享空间方法：

---

数组有两个端点，两个栈有两个栈底，让一个栈的栈底为数组的始端，即下标为0处，另一个的栈底为数组的末端，即下标为n-1处。这样，如果两个栈增加元素，就是两端点向中间延伸。当top1 + 1 == top2 的时候为栈满。

但是这只是针对两个具有相同数据类型的栈的一个设计上的技巧，这种数据结构适合一个栈增长一个栈同时在缩短的情况，就像有卖的同时一定有买，有输的同时一定有赢，适合一种零和博弈。

两栈共享空间的代码实现：

---

#include <iostream>
#include <stdlib.h>
using namespace std;

#define MAXSIZE 20

typedef int SElemType;
typedef struct 
{
    SElemType data[MAXSIZE];
    int top1;//栈1的栈顶指针
    int top2;//栈2的栈顶指针
}SqDoubleStack;

/*初始化栈1和栈2*/
bool InitStack(SqDoubleStack *ds)
{
    cout << "Init Stack ..." << endl;
    ds->top1 = -1;
    ds->top2 = MAXSIZE;

    return true;
}

/*将栈清空*/
bool ClearStack(SqDoubleStack *ds)
{
    cout << "Clear Stack ..." << endl;
    ds->top1 = -1;
    ds->top2 = MAXSIZE;

    return true;
}

/*判断栈是否为空*/
bool IsStackEmpty(SqDoubleStack ds)
{
    if(ds.top1 == -1 && ds.top2 == MAXSIZE)
    {
        return true;
    }
    return false;
}
/*返回栈中元素个数*/
int StackLength(SqDoubleStack ds)
{
    cout << "Stack Length: ";
    return (ds.top1 + 1) + (MAXSIZE - ds.top2);
}
/*插入元素e为新的栈顶元素*/
bool Push(SqDoubleStack *ds, SElemType e, int stackNumber)
{
    if(ds->top1 + 1 == ds->top2)/*栈已满*/
    {
        return false;
    }

    if(stackNumber == 1)
    {
        ds->data[++ds->top1] = e;
    }
    else if(stackNumber == 2)
    {
        ds->data[--ds->top2] = e;
    }

    return true;
}
/*删除栈顶元素，用e返回其值*/
bool Pop(SqDoubleStack *ds, SElemType *e, int stackNumber)
{
    if(stackNumber == 1)
    {
        if(ds->top1 == -1)
        {
            return false;
        } 
        *e = ds->data[ds->top1--];
    }
    else if(stackNumber == 2)
    {
        if(ds->top2 == MAXSIZE)
        {
            return false;
        }
        *e = ds->data[ds->top2++];
    }
    return true;
}
/*获取栈顶元素*/
bool GetTop(SqDoubleStack ds, SElemType *e, int stackNumber)
{
    if(stackNumber == 1)
    {
        if(ds.top1 != -1)
        {
            *e = ds.data[ds.top1];
            cout << "Get Top1 Item: " << *e << endl; 
            return true;
        }
        return false;
    }
    else if(stackNumber == 2)
    {
        if(ds.top2 != MAXSIZE)
        {
            *e = ds.data[ds.top2];
            cout << "Get Top2 Item: " << *e << endl; 
            return true;
        }
        return true;
    }
    else
    {
        cout << "Stack Num must be 1 or 2!" << endl;
        return false;
    }
}//GetToop()
/*遍历整个栈，一次输出各个元素*/
bool StackTraverse(SqDoubleStack ds)
{
    cout << "Traverse Stack ..." << endl;
    if(IsStackEmpty(ds))
    {
        return false;
    }
    cout << "Stack 1: ";
    for(int i = ds.top1; i >= 0; i--)
    {
        cout << ds.data[i] << ' ';
    }
    cout << endl;

    cout << "Stack 2: ";
    for(int j = ds.top2; j < MAXSIZE; j++)
    {
        cout << ds.data[j] << ' ';
    }
    cout << endl;
     
    return true;
}

void main()
{
    SqDoubleStack ds;
    InitStack(&ds);

    for(int i = 0; i < 5; i++)
    {
        Push(&ds, i, 1);
    }
    for(int j = 5; j < 10; j++)
    {
        Push(&ds, j, 2);
    }

    StackTraverse(ds);

    int result;
    Pop(&ds, &result, 1);
    Pop(&ds, &result, 2);
    StackTraverse(ds);
    GetTop(ds, &result, 1);
    GetTop(ds, &result, 2);
    if (!IsStackEmpty(ds))
    {
        cout << StackLength(ds) << endl;
    }
    ClearStack(&ds);

    system("pause");
}

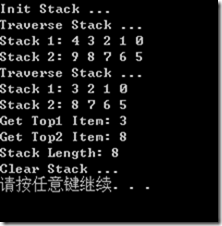
执行结果：