802. 找到最终的安全状态 力扣（中等） 拓扑，开始没想到

802. 找到最终的安全状态

在有向图中，以某个节点为起始节点，从该点出发，每一步沿着图中的一条有向边行走。如果到达的节点是终点（即它没有连出的有向边），则停止。

对于一个起始节点，如果从该节点出发，无论每一步选择沿哪条有向边行走，最后必然在有限步内到达终点，则将该起始节点称作是 安全 的。

返回一个由图中所有安全的起始节点组成的数组作为答案。答案数组中的元素应当按 升序 排列。

该有向图有 n 个节点，按 0 到 n - 1 编号，其中 n 是 graph 的节点数。图以下述形式给出：graph[i] 是编号 j 节点的一个列表，满足 (i, j) 是图的一条有向边。 

示例 1：

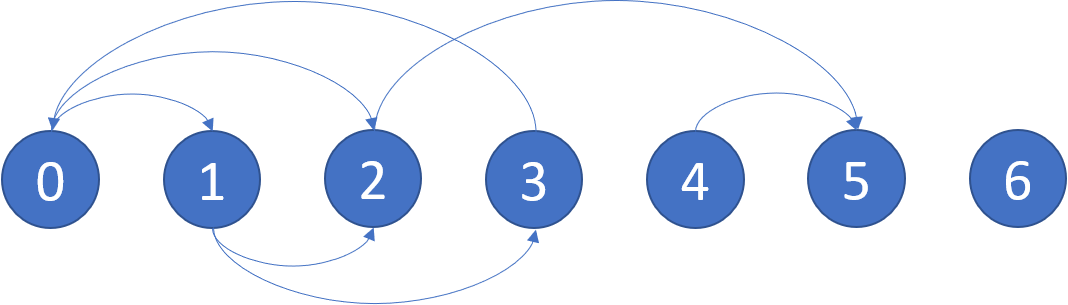
输入：graph = [[1,2],[2,3],[5],[0],[5],[],[]]
输出：[2,4,5,6]
解释：示意图如上。

题解：

学习要点：拓扑排序可以判断是否有环

构建反向的图，拓扑。从终点开始寻找安全点

代码：

class Solution {
public:
    vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
     int f[10005];
     memset(f,0,sizeof(f));
     vector<int>  a[10005],res;
     for(int i=0;i<graph.size();i++)   //反向建图，反向拓扑
       for(auto j: graph[i])
       {
           f[i]++;
           a[j].push_back(i);
       }
           
    queue<int> Q;
    for(int i=0;i<graph.size();i++)
       if (f[i]==0)  {Q.push(i);  res.push_back(i);}  // 将入度为0的点，放入队列中
    while(!Q.empty())
    {
        int p=Q.front();
        Q.pop();
        for(auto i:a[p])   //  删去p节点指向的所有边
        {
            f[i]--;
            if(f[i]==0) 
            {
                Q.push(i);    // 加入入度为0的点
                res.push_back(i);   //  该点可以到达最终点，即该点为安全点
            }
        }
    }
    sort(res.begin(),res.end());
    return res;
    }
};