题目
题目链接:https://www.luogu.com.cn/problem/P4292
X 国遭受了地震的重创, 导致全国的交通近乎瘫痪,重建家园的计划迫在眉睫。X 国由 (N) 个城市组成, 重建小组提出,仅需建立 (N-1) 条道路即可使得任意两个城市互相可达。于是,重建小组很快提出了一个包含 (N-1) 条道路的方案,并满足城市之间两两可达,他们还计算评估了每条道路 (e) 建设之后可以带来的价值 (v(e))。
由于重建计划复杂而艰难,经费也有一定限制。因此,政府要求第一期重建工程修建的道路数目为 (k) 条,但需满足 (L leq k leq U),即不应少于(L) 条,但不超过 (U) 条。同时,为了最大化利用率,要求建设的这些道路恰好组成一条简单路径,即所建设的 (k) 条路径可以构成一个排列 (e_1 = (p_1, q_1), e_2 = (p_2, q_2), cdots , e_k = (p_k, q_k)), 对于 (1 leq i < k), 有((q_i = p_{i+1}))。
重建小组打算修改他们的原有方案以满足要求,即在原有的 (N-1) 条道路中寻找一条路径 (S) 作为新的方案,使得新方案中的道路平均价值
最大。这里 (v(e)) 表示道路 (e) 的价值,(|S|) 表示新方案中道路的条数。请你帮助重建小组寻找一个最优方案。 注: 在本题中 (L) 和 (U) 的设置将保证有解。
(nleq 100000)。
思路
首先很显然需要套上一个二分答案,边权减去 (mid) 后转化为求路径长度在 ([L,R]) 中的最大值。
长剖,对于点 (x),先把他的长儿子跑一遍,然后考虑他的轻儿子 (y) 的贡献。
枚举 (y) 的子树中链的深度 (j),那么 (x) 其他已经便利过的子树中所取的链长度应该在 ([max(0,L-j-1),min( ext{maxd}_x,R-j-1)]) 中,其中 ( ext{maxd}_x) 表示 (x) 子树中深度最大的点到 (x) 的距离。
那么问题变为如何在 (O(log n)) 的时间内得到 (x) 已经便利过子树中距离 (x) 长度在区间内的路径的边权最大值。
维护一棵线段树,对于一个 (x) 子树已经遍历过的节点 (z),记 ( ext{id}_z) 表示 (z) 在长剖后的 dfs 序。那么线段树上区间 ([ ext{id}_z, ext{id}_z]) 则表示下图红框中所有节点到 (x) 的距离最大值。
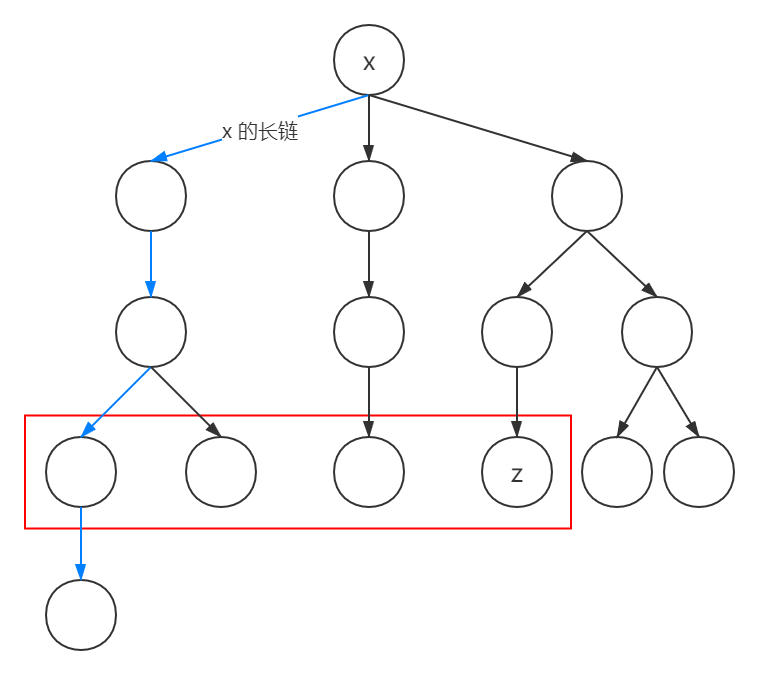
也就是在 (z) 之前遍历到,(x) 子树内所有与 (z) 深度相同的点,到 (x) 距离的最大值。
这样的话有两个优点:同一条长链上的,深度连续的点在线段树上的编号连续;且我们每次从一个轻儿子回到其父亲节点的时候不用清空线段树,并且信息可以正确继承。
然后线段树维护区间最大值即可。
我们枚举的深度之和就是所有长链的长度之和,显然是 (O(n)) 的,所以对于一次 check 我们的复杂度是 (O(nlog n)) 的,再算上二分,最终的时间复杂度是 (O(nlog nlog r)) 的,其中 (r) 是二分上界。
代码
#include <bits/stdc++.h>
using namespace std;
const int N=100010;
const double eps=1e-5,Inf=1e18;
int n,L,R,tot,head[N],dep[N],maxd[N],son[N],id[N],pos[N];
double ans,dis[N];
struct edge
{
int next,to,dis1;
double dis;
}e[N*2];
void add(int from,int to,int dis)
{
e[++tot]=(edge){head[from],to,dis,0.0};
head[from]=tot;
}
struct SegTree
{
double maxv[N*4];
void clear(int x,int l,int r)
{
maxv[x]=-Inf;
if (l==r) { pos[l]=x; return; }
int mid=(l+r)>>1;
clear(x*2,l,mid); clear(x*2+1,mid+1,r);
}
void update(int x,int l,int r,int k,double v)
{
maxv[x]=max(maxv[x],v);
if (l==r) return;
int mid=(l+r)>>1;
if (k<=mid) update(x*2,l,mid,k,v);
else update(x*2+1,mid+1,r,k,v);
}
double query(int x,int l,int r,int ql,int qr)
{
if (ql<=l && qr>=r) return maxv[x];
int mid=(l+r)>>1; double res=-Inf;
if (ql<=mid) res=max(res,query(x*2,l,mid,ql,qr));
if (qr>mid) res=max(res,query(x*2+1,mid+1,r,ql,qr));
return res;
}
}seg;
void prework()
{
ans=-Inf; tot=0;
seg.clear(1,1,n);
}
void dfs1(int x,int fa)
{
dep[x]=dep[fa]+1;
for (int i=head[x];~i;i=e[i].next)
{
int v=e[i].to;
if (v!=fa)
{
dfs1(v,x);
if (maxd[v]+1>maxd[x])
maxd[x]=maxd[v]+1,son[x]=i;
}
}
}
void dfs2(int x,int fa)
{
id[x]=++tot;
if (son[x])
{
int v=e[son[x]].to;
dis[v]=dis[x]+e[son[x]].dis;
dfs2(v,x);
}
seg.update(1,1,n,id[x],dis[x]);
for (int i=head[x];~i;i=e[i].next)
{
int v=e[i].to;
if (i!=son[x] && v!=fa)
{
dis[v]=dis[x]+e[i].dis;
dfs2(v,x);
for (int j=0;j<=maxd[v];j++)
{
int ql=id[x]+max(0,L-j-1),qr=id[x]+min(maxd[x],R-j-1);
ans=max(ans,seg.maxv[pos[id[v]+j]]+seg.query(1,1,n,ql,qr)-2.0*dis[x]);
}
for (int j=0;j<=maxd[v];j++)
seg.update(1,1,n,id[x]+j+1,seg.maxv[pos[id[v]+j]]);
}
}
ans=max(ans,seg.query(1,1,n,id[x]+L,id[x]+min(maxd[x],R))-dis[x]);
}
int main()
{
memset(head,-1,sizeof(head));
scanf("%d%d%d",&n,&L,&R);
for (int i=1,x,y,z;i<n;i++)
{
scanf("%d%d%d",&x,&y,&z);
add(x,y,z); add(y,x,z);
}
dfs1(1,0);
double l=0,r=1e6,mid;
while (r-l>eps)
{
prework();
mid=(l+r)/2.0;
for (int i=1;i<=2*(n-1);i++)
e[i].dis=1.0*e[i].dis1-mid;
dfs2(1,0);
if (ans>=0) l=mid;
else r=mid;
}
printf("%.3lf",l);
return 0;
}