HDU 4328 Cut the cake

Cut the cake

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1250    Accepted Submission(s): 489

Problem Description：

Mark bought a huge cake, because his friend ray_sun’s birthday is coming. Mark is worried about how to divide the cake since it’s so huge and ray_sun is so strange. Ray_sun is a nut, you can never imagine how strange he was, is, and going to be. He does not eat rice, moves like a cat, sleeps during work and plays games when the rest of the world are sleeping……It is not a surprise when he has some special requirements for the cake. A considering guy as Mark is, he will never let ray_sun down. However, he does have trouble fulfilling ray_sun’s wish this time; could you please give him a hand by solving the following problem for him?
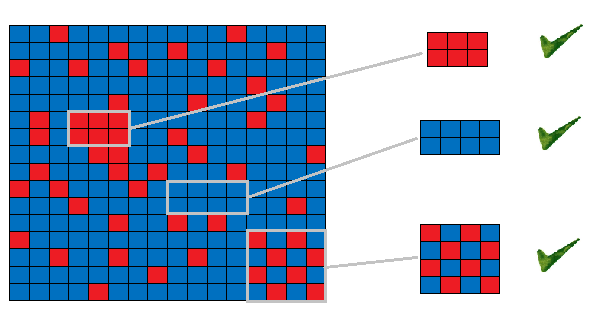
  The cake can be divided into n*m blocks. Each block is colored either in blue or red. Ray_sun will only eat a piece (consisting of several blocks) with special shape and color. First, the shape of the piece should be a rectangle. Second, the color of blocks in the piece should be the same or red-and-blue crisscross. The so called ‘red-and-blue crisscross’ is demonstrated in the following picture. Could you please help Mark to find out the piece with maximum perimeter that satisfies ray_sun’s requirements?

 

Input

The first line contains a single integer T (T <= 20), the number of test cases.
  For each case, there are two given integers, n, m, (1 <= n, m <= 1000) denoting the dimension of the cake. Following the two integers, there is a n*m matrix where character B stands for blue, R red.

Output

For each test case, output the cased number in a format stated below, followed by the maximum perimeter you can find.

Sample Input

2 1 1 B 3 3 BBR RBB BBB

Sample Output

Case #1: 4 Case #2: 8

Author

BJTU

Source

2012 Multi-University Training Contest 3

Recommend

zhoujiaqi2010   |   We have carefully selected several similar problems for you:  4321 4366 4335 4377 4371 

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
#include<algorithm>
#define N 1010
int n,m,h[N][N],l[N][N],r[N][N];
char g[N][N];
int ans=0,tmpl[N],tmpr[N];
void solve(char key){
    memset(h,0,sizeof(h));
    memset(l,0,sizeof(l));
    memset(r,0,sizeof(r));
    int mx=0;
    for(int i=1;i<=m;i++){
        l[0][i]=0;r[0][i]=m;
    }
    for(int i=1;i<=n;i++){
        int tmp=1;
        for(int j=1;j<=m;j++){
            if(g[i][j]!=key)tmp=j+1;
            else tmpl[j]=tmp;
        }
        tmp=m;
        for(int j=m;j>=1;j--){
            if(g[i][j]!=key) tmp=j-1;
            else tmpr[j]=tmp;
        }
        //记录好了一个点能到达的 最左边 和最右边,
        //接下来就是dp了
        for(int j=1;j<=m;j++){
            if(g[i][j]!=key){
                l[i][j]=1;h[i][j]=0;r[i][j]=m;
                continue;
            }
            h[i][j]=h[i-1][j]+1;
            l[i][j]=max(l[i-1][j],tmpl[j]);
            r[i][j]=min(r[i-1][j],tmpr[j]);
            mx=max(2*(r[i][j]-l[i][j]+1+h[i][j]),mx);
        }
    }
    ans=max(ans,mx);
}
int main()
{
    int T,tt=1;scanf("%d",&T);
    for(int tz=1;tz<=T;tz++){
        ans=0;
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;i++)
          scanf("%s",g[i]+1);
        solve('B');solve('R');
        for(int i=1;i<=n;i++)
          for(int j=1;j<=m;j++)
            if((i+j)%2==0){
              if(g[i][j]=='B')g[i][j]='R';
              else g[i][j]='B';
            }
        solve('B');solve('R');
        printf("Case #%d: ",tt++);
        printf("%d
",ans);
    }
    return 0;
}

思路：悬线法~~~~DP求满足题意的最大子矩阵的边长