支持向量机（SVM）（六）--核函数

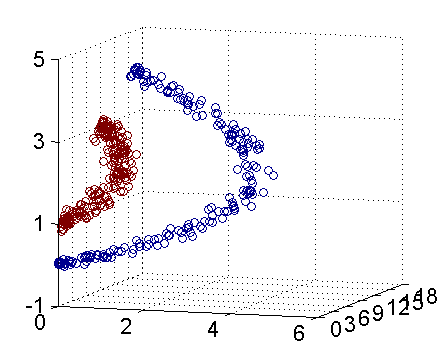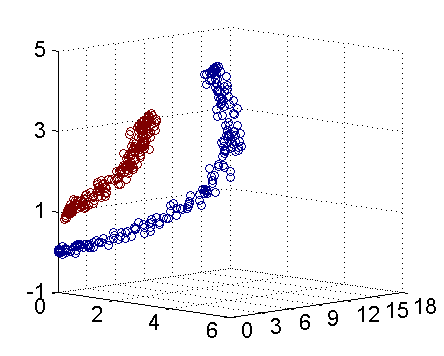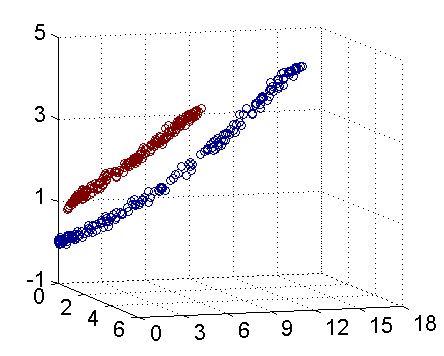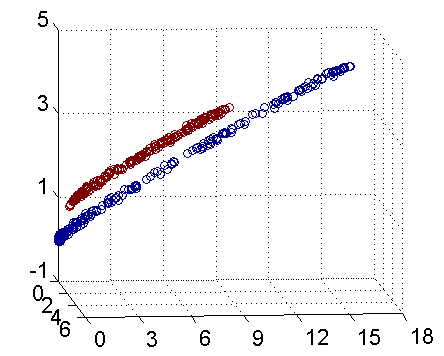
在线性SVM一文中提到，线性可分时b的求解。但是在线性不可分情形下，如下二维平面图，无法找到一条直线将红蓝色样本点完全分开

SVM提出了一个解决办法，就是把低维的特征投影到高维空间使得样本可以一分为二，例如下动图所示。

回顾上一节软间隔，我们得到优化目标

$underset{a}{min}=frac{1}{2}sum sum a_{i}a_{j}y_{i}y_{j}x_{i}cdot x_{j}-sum a_{i}$

　　　　　　　　$s.t sum a_{i}y_{i}=0$

　　　　　　　　$0leqslant alpha _{i}leqslant C$

那么按照低维到高维的思想， 我们在$x_{i}cdot x_{j}$一个函数变化$phi $,使得样本维度变高，然后再做內积，即$phi(x_{i}) cdotphi(x_{j})$

也就是$underset{a}{min}=frac{1}{2}sum sum a_{i}a_{j}y_{i}y_{j}phi(x_{i}) cdotphi(x_{j})-sum a_{i}$

　　　　　　　　$s.t sum a_{i}y_{i}=0$

　　　　　　　　$0leqslant alpha _{i}leqslant C$

这样似乎简单粗暴地将线性不可分问题就解决了，但是人们很快发现这个方法的缺陷，当样本本身维度就很高时，再将样本特征映射到更高维，

计算量明显增大，甚至出现无穷维。

那么这时候核函数隆重登场！

---

举一个简单例子说明核函数（kernel function）的神奇之处

样本X1（a1，a2），X2（b1,，b2）

将二维特征投影到六维变成

X'1(1,√2a1,√2a2,a1²,a2²,√2a1a2)

X'2(1,√2b1,√2b2,b1²,b2²,√2b1b2)

X1'•X2'=1+2a1b1+2a2b2+a1²b1²+a2²b2²+2a1b1a2b2（高维空间做內积）

设K（X_i,X_j）=(X_i•X_j+1)²=(a1b1+a2b2+1)²=1+2a1b1+2a2b2+a1²b1²+a2²b2²+2a1b1a2b2

可以看出红色部分完全相同。

但是使用核函数求內积时，仅仅输入的是二维数据，但是和高维向量X1'和X2'的內积完全相同。

至于常见的核函数，参考https://blog.csdn.net/kateyabc/article/details/79980880

---

所以我们再将$phi(x_{i}) cdotphi(x_{j})$变成$mathbf{K}（x_{i}，x_{j}）$

整理算法过程：

$underset{a}{min}=frac{1}{2}sum sum a_{i}a_{j}y_{i}y_{j}mathbf{K}（x_{i}，x_{j}）-sum a_{i}$

　　　　　　　　$s.t sum a_{i}y_{i}=0$

　　　　　　　　$0leqslant alpha _{i}leqslant C$

1，根据SMO得到α*

2，根据$w = sum a^{*}y_{i}phi(x_{i})$有$w^{*}phi(x_{j}) = sum a^{*}y_{i}phi(x_{i})phi(x_{j})$,这里不必得到显式的w，而且，$phi(x)$往往我们也不知道

3，根据$0<α_i<C,找到所有支持向量上的点,小标为s，有

$y_{s}left ( sum alpha _{i}y_{i} Kleft ( x_{i},x_{s} ight )+b ight )=1$

其中的$sum a_{i}y_{i}phi(x_{i})phi(x_{j})$为已知，所以可求得b，将b求平均得到b*

4，最终超平面为

$sum alpha ^{*}y_{i}K(x_{i},x_{j})+b^{*}=0$

对于核函数的定义低维的输入空间（欧式空间子集）到高维的希尔伯特空间的映射。参考这篇博文。简单理解不影响理解SVM即可。