菜到只能学文化课
0.新运动学习提纲
- 先找出\(\vec{r}(t),\vec{v}(t),\vec{a}(t)\)的解析式
理解解析式参数的物理意义,与运动画面对应
分析解析式函数性质,定义域,值域,单调性,周期性等和它们对应的物理意义
不分析物理意义就真成数学了 - 分析动力学特征,\(\vec{r}(t),\vec{v}(t),\vec{a}(t)\)的参数由什么决定,受力有什么特点
- 分析功和能的变化
比如,弹簧震动时,动能与弹性势能的相互转化
这其中,分析物理意义是极重要的,理论物理就是先通过数学分析,再进行对物理意义的分析
1.简谐振动
1.1 \(\vec{r}(t)\)
假设物体在一条直线上做简谐振动
把x轴建在这条直线
物体运动轨迹的中间平衡位置为坐标原点(它有种“对称性”)
\(\vec{r}(t)=(A\cos (\omega t+\phi)+b,0)\)
下面通过分析函数的各种性质来找物理意义
1.1.1定义域
\(t\subset[0,\infty]\)
当\(t=0\),物体在初始位置
\(\vec{r}(0)=(A \cos\phi +b,0)\)
1.1.2值域
根据\(\cos\)的性质:
\(x\subset[-A+b,A+b]\)
所以可以看出,\(x=b\)为物体震动的中间平衡位置(以此为对称轴),\(A\)为振幅
整个轨迹长度为\(2A\)
因此,\(b\)的变化只导致整个振动的位置沿x轴平移,不影响运动细节,为了简便,可以让\(b=0\),即物体从坐标原点开始振动,下文的分析都以\(b=0\)进行
那么,化简之后:\(\vec{r}(t)=(A\cos(\omega t+\phi),0)\)
\(t=0\):\(\vec{r}(0)=(A\cos \phi,0)\)
发现\(t=0\),x不一定等于0
所以\(\phi\)决定物体起振位置(因为\(A\)已经是振幅了)
注意,\(b\)决定的是平衡位置,\(\phi\)决定的是初始位置,平衡位置不一定是初始位置
所以:
- \(\phi=0,\vec{r}(0)=(A,0)\),说明物体从右端点起振
- 当\(\phi=\frac{\pi}{2},\vec{r}(0)=(0,0)\),从原点起振
- 当\(\phi=\pi,\vec{r}(0)=(-A,0)\),从左端点起振
1.1.3单调性&周期性
不妨设物体从右端点起振,即\(\phi=0\),这并不影响对运动的分析
则\(\vec{r}(t)=(A\cos \omega t,0)\)
现在\(\omega\)的意义还没找到
讲\(\omega t\)当作一个整体,想象一下\(\cos\)的图像
可以发现,\(\cos(\omega t)\)以\(2\pi\)为周期
\(\cos(\omega t+2n\pi)=\cos\omega t\)
所以\(t\)的周期是\(\dfrac{2\pi}{\omega}\)
所以\(\vec{r}(t)=\vec{r}(t+\dfrac{2n\pi}{\omega})\)
所以振动周期\(T=\dfrac{2\pi}{\omega}\)
也就是说\(\omega\)影响了周期的参数
\(\omega=\dfrac{2\pi}{T}\),称为角频率,相当于圆周运动里的角速度
单调性的意义:单调递增的时候说明在像右动(正方向,\(t\subset [\dfrac{\pi}{\omega}+\dfrac{2n\pi}{\omega},\dfrac{2\pi}{\omega}+\dfrac{2n\pi}{\omega}]\))
单调递减时说明在向左动(负方向,\(t\subset [0+\dfrac{2n\pi}{\omega},\dfrac{\pi}{\omega}+\dfrac{2n\pi}{\omega}]\))
1.1.4所以可以给出结论
\(\vec{r}(t)=(A\cos (\omega t+\phi)+b,0)\)中:
- \(A\)表示振幅
- \(\omega\)为角频率,决定周期,\(\omega=\dfrac{2\pi}{T}\)
- \(\phi\)叫初始相位,决定初始位置
- \(b\)决定平衡位置,可以令整个运动平移
- \((\omega t+\phi)\)称为相位
1.1.5简谐振动和匀速圆周运动
每个简谐振动,都对应一个圆周运动
给出简谐运动与圆周运动的对应
仔细想一想发现下面这些东西还是挺好理解的
- \(\vec{r}(t)=(A\cos\omega t,0)\)对应圆周运动\(\vec{r}(t)=(A\cos\omega t,A\sin\omega t)\)
- \(\vec{r}(t)=(A\cos (\omega t+\phi)+b,0)\)对应圆周运动中\(\vec{r}(t)=(A\cos (\omega t+\phi)+b',A\sin(\omega t+\phi)+b')\)
- \((b,b')\)对于简谐振动时平衡位置,对于圆周运动是就是圆心
- \(A\)对应圆周运动中的圆周半径
- 相位对应圆周运动中的转角,初相位对应初始角度
- \(\omega\)当然也就是对应角速度
所以,其实简谐运动就是匀速圆周运动在坐标轴的投影,在上面第二三个式子中的\(b'\)其实就是在\(y=b'\)投影
\(\vec{r}\)终于结束了,然而还有\(\vec{v}\)和\(\vec{a}\)....
1.2\(\vec{v}(t)\)
通过求导:
\(\vec{v}(t)=\dfrac{d\vec{r}(t)}{dt}=(-A\omega\sin(\omega t+\phi),0)\)
1.2.1值域
\(v_x\subset[-\omega A,\omega A]\)
所以速度大小是从0取到\(\omega A\)
考虑这些特殊值取到的条件
还是要想象一下\(\sin\)的图像
- \(\omega t+\phi=-\frac{\pi}{2}+2n\pi\)
此时为平衡位置,\(v\)取到\(\omega A\) - \(\omega t+\phi=\frac{\pi}{2}=2n\pi\)
此时为平衡位置,\(v\)取\(-\omega A\) - \(\omega t+\phi=n\pi\)
此时在左右端点,\(v\)取0
1.2.2周期性
\(\vec{v}(t)\)的变化周期与\(\vec{r}(t)\)相同(就是多乘了一个\(\omega\)),\(T=\dfrac{2\pi}{\omega}\)
1.2.3定义域
\(t\subset[0,+\infty]\)
\(t=0,\vec{v}(t)=(-A\omega\sin\phi,0)\)
\(\phi\)为速度的初始相位
1.2.4\(\vec{v}\)和\(\vec{r}\)的映射关系
已知\(\vec{v}\),相当于已知\(\sin(\omega t+\phi)\)
要推\(\vec{r}\),相当于要推\(\cos(\omega t+\phi)\)
所以,\(\cos(\omega t+\phi)=\pm\sqrt{1-\sin^2(\omega t+\phi)}\),这是通过诱导公式推出
所以,\(\vec{v}\)确定时,物体位于关于平衡位置对称的两个点(可以推知动能与弹性势能的能量守恒)
反之,\(\vec{r}\)确定时,\(\vec{v}\)的大小可以被确定,但方向不一定
想象一个物体振动的画面,在同一个位置,物体有可能朝边界位置运动,也有可能朝平衡位置运动
1.3\(\vec{a}(t)\)
这个直接简略的写了
还是求导:
\(\vec{a}(t)=\dfrac{d\vec{v}}{dt}=(-\omega^2A\cos(\omega t+\phi),0)=-\omega^2\vec{r}(t)\)
也是假设了\(b=0\)
所以可以得出推论:
- \(\vec{a}\)始终与\(\vec{r}\)反向
- \(\vec{a},\vec{r}\)的映射是一对一的
- \(a_x\subset[-\omega^2A,\omega^2A]\)
当物体位于平衡位置,\(a=0\),当物体位于边界,\(a=\omega^2A\)
所以现在有了一堆 关于平衡树 关于平衡位置的性质:
- 它是整个简谐运动的对称的
- 速度最大
- 加速度为0
- 又根据牛二定律,物体受平衡力
那么我们可以根据最后一条,在找弹簧的平衡位置时,就是去找它受平衡力的点
比如竖直的弹簧,它静止的那个长度的点,才是平衡位置
2.简谐振动的运动学特征
这类题一般可以先把\(\vec{r}(t)\)找出来,根据它求解
2.1
\(\vec{F}=m\vec{a}=-m\omega^2\vec{r}\)
\(=(-m\omega^2A\cos(\omega t+\phi),0)\)
\(=-m\omega^2\vec{r}\)
容易联想到 容易吗 胡可定律
链接弹簧的振子受的弹力:\(\vec{F}=-k\vec{r}\)
所以,说明弹簧振子所受弹力可使其做简谐振动,\(k=m\omega ^2\)
所以,\(\omega=\sqrt{\dfrac{k}{m}}\),符号当然是要舍弃的
那么,\(T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{m}{k}}\)
这就说明了,弹簧振子简谐振动的周期由振子质量,和弹簧弹性系数决定
随\(m\)增加,\(T\)增大,这是因为质量越大,惯性越大,越难改变它的运动状态,到了边界时,有一种“刹不住车”的状态,那运动距离就增长,时间当然也就更长
同样,如果\(k\)减小,就是弹簧比较软,也是这种“刹不住车”的情况,\(T\)也就增大
2.2决定这些参数的因素
\(\vec{r}=(A\cos(\omega t+\phi),0)\)
其中,\(\omega\)由\(k\)和\(m\)决定,也就是上面描述的
那么\(A\)和\(\phi\)呢?
\(A,\phi\)相当于两个待定系数,由两个初始条件决定
\(\vec{r}(0)\)决定了\(\phi\),但可能会相差\(\pi\)的相位(往左动或是往右动)
决定\(A\)的因素:比如我把弹簧拉到\(5cm\),那么弹簧的\(A\)即\(5cm\),如果我把它拉到\(5cm\)并给它一个初速度,那么它的\(A\)就也不是\(5cm\)了,而且当速度一定,弹簧的\(k\)不一样\(A\)也会有差别
所以,\(A\)是由\(E_{total}\)决定(也就是上面那三个因素的综合)
3关于弹簧势能
3.1其大小的推导
假设一个弹簧振子在水平面做简谐振动(不考虑重力势能的变化),机械能守恒,所以动能和弹性势能的和是一常数
\(\vec{r}(t)=(A\cos\omega t,0)\),当\(t=0,\vec{r}=(A,0)\)
此时速度为0,所有能量都是弹性势能
当\(t=\frac{T}{4}\)(\(T\)是周期),振子在平衡位置,弹性势能肯定为0,所有能量都为动能
又因为\(\vec{v}(t)=(-A\omega\sin\omega t,0)\),所以当\(t=\frac{T}{4},v=A\omega\)
所以结合上面两种情况,并运用\(\omega=\sqrt{\frac{k}{m}}\)做出推导:
\(A\)是振幅,其实也就是弹簧的型变量
所以当型变量为\(\Delta x\)时,弹簧的弹性势能为\(E_p=\dfrac{1}{2}k\Delta x^2\)
3.2那么就可以给出能量转换的总结
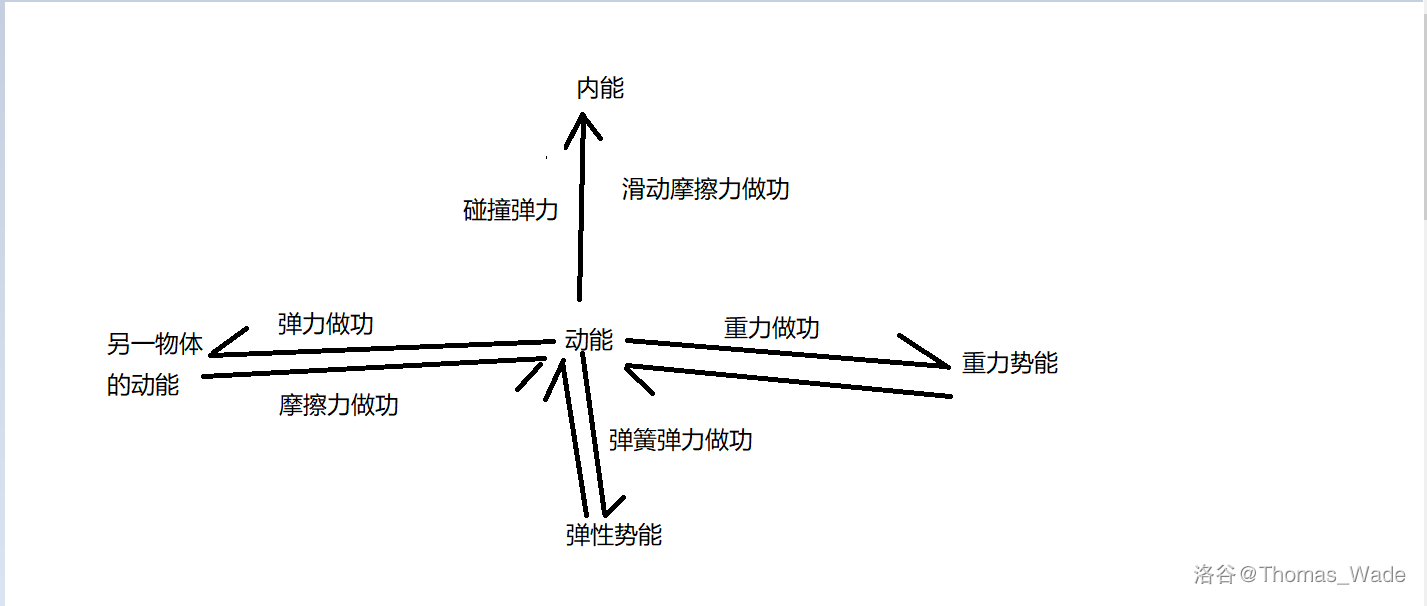
要注意那个内能的箭头是单向的,没有回到动能箭头
3其他东西
3.1对称性
这玩意也不知道在哪说,就放在这吧
首先,运动的轨迹是关于平衡的对称的
那么,关于平衡点对称的两个点,其速度大小是相同的,当然方向可能不同(1.2.4)
对于加速度,是大小方向均相同(1.3)
这个东西在解题里应该是常用的
比如弹簧振动,如果在一端边界的加速度,速度等物理量是相对好求的,那么我们就可以通过求这一端的物理量来知道另一端对应的物理量
3.2\(\omega<0\)
以上我们的讨论中,都假定了\(\omega>0\),那么当\(\omega<0\),它做的运动还是简谐振动吗?物理意义是什么?
首先,因为\(\cos\)是偶函数,所以整个位矢是不变的,肯定还是简谐振动
至于物理意义,之前说简谐振动就是匀速圆周运动在x轴的投影,那么\(\omega<0\)就是说明这个匀速圆周运动的方向发生了改变,变成顺时针(\(\omega>0\)是逆时针)
但即使这个圆周运动的防线改变,它的投影的轨迹是不变的,因此这个位矢是不变的
3.3单摆
单摆这玩意和简谐振动还能联系起来?
这里说的单摆,实际上只是摆动角度极小的情况

当摆动角为\(\theta\),切线方向大小合力即为\(mg\sin\theta=ma\)
然后刚才说了,讨论的是摆动交极小的情况,所以这里用到一个取极限的方法
当\(\theta \rightarrow 0,\sin\theta \rightarrow \theta\)
又由于\(\theta\)是等于弧长除以半径,在\(\theta\)极小的时候弧长和这两点直接连起来的直线可以看作是相等的
那么\(\theta=\dfrac{\Delta x}{l}\),则\(ma=mg\dfrac{\Delta x}{l}\)
所以这里\(k=\dfrac{mg}{l}\),又因为\(\omega=\sqrt{\dfrac{k}{m}},T=2\pi\sqrt{\dfrac{m}{k}}\)
所以把\(k\)带进去就是\(T=2\pi\sqrt{\dfrac{l}{g}}\)
表明当\(\theta\)较小,单摆可以看作简谐振动,周期的公式
这个式子当把摆长和周期测出来,就能用来测重力加速度
同时,也说明单摆周期只与摆长有关
3.4回复力
指的是使振子返回平衡位置,并总指向平衡位置的力
没错一开始我居然不知道回复力是个啥
3.5关于解题
首先还是要理解这个运动的本质之后再去考虑题
如果能用守恒,首先考虑的肯定是用守恒,这一般是最简单的方法
这里说的守恒是指的能量,动量,角动量的守恒虽然后面俩还不会
关于如何判定守恒,要先分析做功的力的种类,判断能量守恒的范围,具体的在上面那张图里说过了
一般不太难的应该是可以把它的\(\vec{r}\)求出来
老师这么说的,然而我并没有发现哪个题用这个方法能更简单
或者是我太菜做的题太少
求的方法大概就是把\(\vec{r}\)先写出来,然后通过条件慢慢去确定其中每一个参数
另一个就是刚才说的对称性
其它如果还有别的发现或总结的好办法,会补充进来
然后呢?
然后就没了
一开始听课的时候记在了纸上,之后发现做作业的时候完全不会
于是听着回放又在blog里整理了一遍笔记
但怎么感觉那些题还是不会