这部分内容来源于Andrew NG老师讲解的 machine learning课程,包括异常检测算法以及推荐系统设计。异常检测是一个非监督学习算法,用于发现系统中的异常数据。推荐系统在生活中也是随处可见,如购物推荐、影视推荐等。课程链接为:https://www.coursera.org/course/ml
(一)异常检测(Anomaly Detection)
举个栗子:
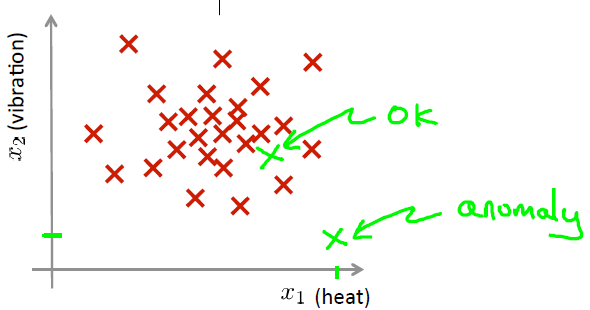
我们有一些飞机发动机特征的sample:{x(1),x(2),...,x(m)},对于一个新的样本xtest,那么它是异常数据么(这个数据不属于该组的几率怎样)?我们可以构建一个模型p(x),来计算测试数据是否为异常数据.从图中可见,若数据落在蓝色圈内,则属于该组的可能性较高,若落于蓝色圈外,则属于该组的几率较低。
 |
 |
这种方法为密度估计,表达式如下:
if p(xtest) ≤ ε → anomaly
if p(xtest) > ε → normal
异常检测应用:
可以用来识别欺骗。例如在online采集的数据中,特征向量可能包括:用户多久登陆一次,点击过的页面,发帖数量,打字速度等。我们可以根据这些特征来构建模型,用来识别不符合该模式的用户;再者在数据中心里,特征向量可能包括:内存使用情况、CPU负载、被访问的磁盘数、网络通信量等。构建模型从而判断计算机是否出错。
高斯分布
若变量X符合高斯分布,记为 x~N(μ,σ2),概率密度函数:![]()
其中μ和σ2计算方法为:![]()
PS:ML中对于σ2 通常除以m,而统计学中通常除以(m-1)。
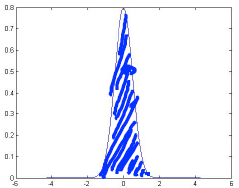
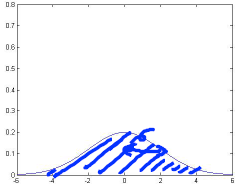
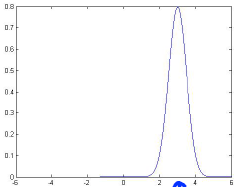
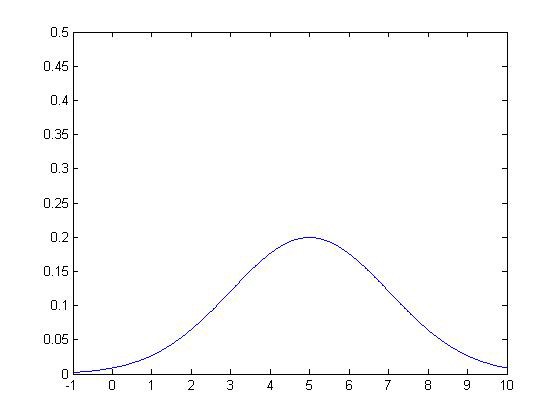
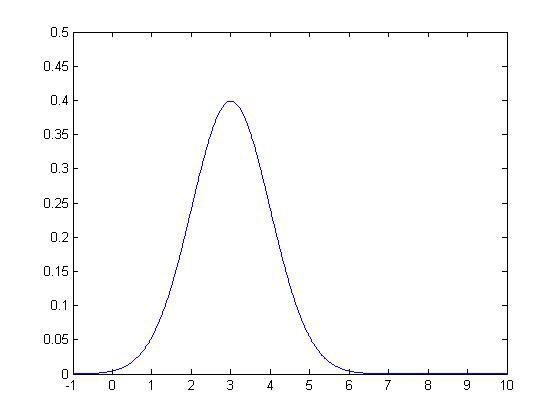
下面是几个高斯分布的例子:
|
μ = 0 σ = 1
|
μ = 0 σ = 0.5
|
μ = 0 σ = 2
|
μ = 3 σ = 0.5
|
异常检测算法
1.给定数据集{x(1),x(2),...,x(m)},计算每个特征的μ和σ2:
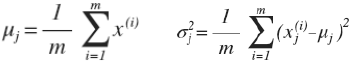
2.给定测试数据x,根据模型计算p(x):
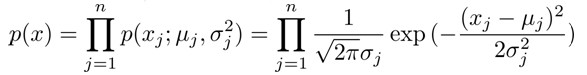
例如,若训练集又两维特征x1,x2组成,其中x1和x2的μ和σ2分别为:μ1=5,σ1 =2;μ2=3,σ2 =1。分布情况如下所示。
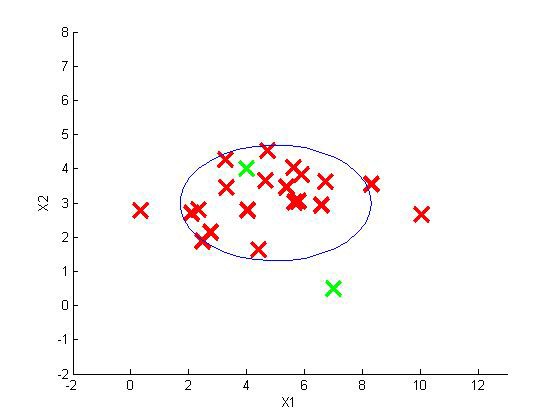 |
|
则模型p(x)函数如下图的三围图像所示,z轴为估计的p(x)值:
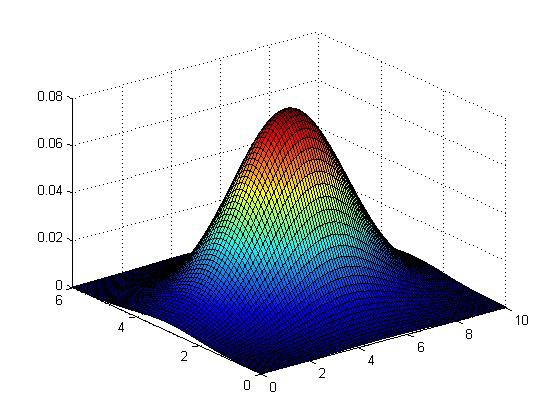
异常检测系统评价
和我们之前学习的监督学习一样,我们需要评估该异常检测系统,但是异常检测算法是unsupervised,即我们无法根据y值来评估预测数据。那么我们就从带标记的(异常或正常)数据入手,假设给定一些有label的数据(若是正常数据则y=0,异常数据则y=1),从中选择一部分正常数据来构成Training set,用剩余的正常数据和异常数据来构成Cross validation set 和 test set。
例如:在飞机引擎的问题中,我们有10000台正常引擎和20台异常引擎。我们这样分配:
- Training set:6000台正常引擎
- CV:2000台正常引擎和10台异常引擎
- Test set:2000台正常引擎和10台异常引擎
评价方法:
1.根据Training set,估计特征的μ和σ2,构建p(x)函数;
2.在CV/Test set上面使用不同的ε作为阈值,预测数据,并根据F1值(或查准率与查全率比值)来选择合适的ε。
异常检测 vs 监督学习
| 异常检测 | 监督学习 |
| 正例很少(y=1大约0-20个),大量负例(y=0) | 有大量正例和负例 |
| 异常种类很多,很难根据较少的异常数据来训练算法 | 有足够多的正例用于训练算法 |
| 未来遇到的异常可能与训练集中的异常非常不同 | 未来遇到的正例与训练集中的非常相似 |
|
eg: 欺诈行为检测、 生产(飞机引擎)、 检测数据中心的计算机运行情况 |
eg: 邮件过滤 天气预测 肿瘤分类 |
特征选择
对于异常检测,特征选择至关重要。之前我们假设异常检测数据符合高斯分布,那么如果现实数据不符合高斯分布呢,虽然异常检测算法也可以正常工作,但是最好将数据转换成高斯分布,如使用对数函数:x←log(x+c),其中c为常数;或使用幂指数:x←xc,其中c为0-1之间的分数。

误差分析:
- 我们通常希望:对于normal,p(x)较大;对于anomalous,p(x)较小。
而一个常见的问题是p(x)对于normal或者anomalous都比较大,那么如何解决呢?
我们可以增加一些特征,或者将一些相关的特征进行组合,这些新的他正可以帮助我们进行更好的异常检测。例如,在数据中心检测计算机状况的问题中,我们可以使用cpu负载与网络通信量之比作为新的特征,若该值特别大则可能说明计算机出现了异常。
多元高斯分布(Mul-variate Gaussian distribution)
在使用高斯分布模型进行异常检测时,可能会出现这样的情况:假设我们有两个特征x1和x2,这两个特征的值域范围较大,而一般的高斯分布模型会尝试同时抓住两个特征,从而创造出一个更大的边界,如图中紫色所示边界,可以看出绿色的样本点可能是异常数据,但是它却处于正常的范围内。那么多元高斯分布会构建蓝色所示的边界。
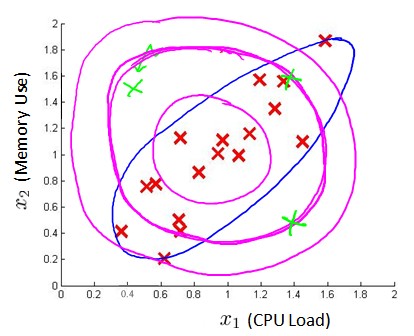
- 通常的高斯分布模型中,我们计算p(x)的方法是分别计算每个特征对应的几率累乘起来:
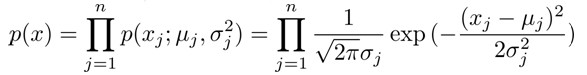
- 在多元高斯分布中,我们将构建特征协方差矩阵,即所有特征放在一起计算p(x):
1. 计算所有特质的平均值µ(µ是一个向量),再计算协方差矩阵。
![]()
2. 计算多元高斯分布的p(x):
![]()
PS:其中|Σ|是矩阵模值,在Octave中用 det(sigma)计算;Σ-1是逆矩阵。那么想要使用多元高斯分布,Σ必须可逆。
协方差矩阵对模型的影响:

分析:
- 图1 是一个一般的高斯分布模型;
- 图2 通过协方差矩阵,使得特征x1拥有较小的偏差,保持特征x2不变;
- 图3 通过协方差矩阵,使得特征x2拥有较小的偏差,保持特征x1不变;
- 图4 通过协方差矩阵,不改变两个特征的原有偏差,增加两者正相关性;
- 图5 通过协方差矩阵,不改变两个特征的原有偏差,增加两者负相关性;
原高斯分布模型与多元高斯分布模型的关系:
显而易见,当协方差矩阵只在对角线上有非零的值时,即为原高斯分布模型,所以原高斯分布模型是多元高斯分布模型的一个子集。
| 原高斯分布模型 | 多元高斯分布模型 |
| 不能捕捉特征间的相关性,可以通过将特征线性组合来解决 | 自动捕捉特征间的相关性 |
| 计算代价低,适应大规模特征 | 计算代价高 |
| 训练集较小时也适用 | 必须有m>n,否则协方差矩阵不可逆,通常要m>10n,另外特征荣誉也会导致协方差矩阵不可逆。 |
PS:
- 原高斯分布模型被广泛使用,若特征之间存在关联,则可以通过构造新的特征来解决;
- 如果训练集不是太大,且没有太多的特征,我们可以使用多元高斯分布模型;
(二)推荐系统(Recommender Systems)
问题描述
假设我们现在有5部电影和4个用户,以及这四个用户对看过电影的评分。前三部是爱情片,后两部是动作片。从表格中我们可以看出Alice和Bob似乎喜欢看爱情片,而Carol和Dave似乎喜欢动作片。我们可以根据一些算法来预测他们会给没看过的电影打多少份,作为推荐的依据。
| Movie | Alice(1) | Bob(2) | Carol(3) | Dave(4) |
| Love at last | 5 | 5 | 0 | 0 |
| Romance forever | 5 | ? | ? | 0 |
| Cute puppies of love | ? | 4 | 0 | ? |
| Nonstop car chases | 0 | 0 | 5 | 4 |
| Swords vs. karate | 0 | 0 | 5 | ? |
符号说明:
- nu:no.users
- nm:no.movies
- r(i,j):用户i是否给电影j评过分,若是则r(i,j)=1
- y(i,j):用户i对电影j的评分
- m(j):用户评分过的电影总数
练习:

基于内容的推荐系统(Content-based recommendations)
现在我们假设每部电影有两个特征:x1代表浪漫程度,x2代表动作程度。
| Movie | Alica(1) | Bob(2) | Carol(3) | Dave(4) |
x1(romance) |
x2(action) |
| Love at last | 5 | 5 | 0 | 0 | 0.9 | 0 |
| Romance forever | 5 | ? | ? | 0 | 1.0 | 0.01 |
| Cute puppies of love | ? | 4 | 0 | ? | 0.99 | 0 |
| Nonstop car chases | 0 | 0 | 5 | 4 | 0.1 | 1.0 |
| Swords vs. karate | 0 | 0 | 5 | ? |
0 | 0.9 |
- θ(j):用户j的参数向量
- x(i):电影i的特征向量
我们预测用户j对电影i的评分为:(θ(j))T(x(i))
Cost Function: ![]() (针对用户j)
(针对用户j)
Cost Function: 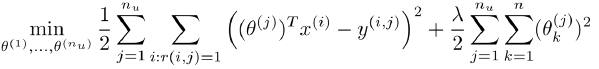 (针对所有用户)
(针对所有用户)
Gradient Descent Update:
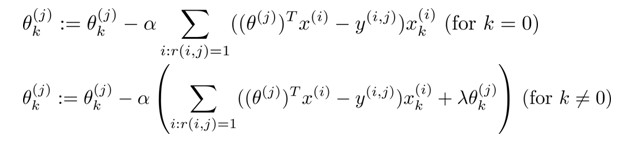
其中i:r(i,j)=1表示我们只计算那些用户j评分过的电影,在一般的linear regression模型中,误差项和归一项都应乘以 1/2m,这里我们统一将m去掉,并且不对θ0进行归一化。
练习:

协同过滤算法(Collaborative filtering algorithm)
对协同过滤,这里有一个比较全面的说明,可供参考:
http://www.ibm.com/developerworks/cn/web/1103_zhaoct_recommstudy2/index.html
在之前的基于内容的推荐系统中我们知道,如果我们掌握电影的可用特征,则可以训练出每个用户的参数;相反如果我们掌握了用户参数,则可以训练出电影的特征。
(1)Given x(1),...,x(nm), estimate θ(1),...,θ(nu):
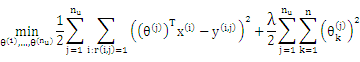
(2)Given θ(1),...,θ(nu), estimate x(1),...,x(nm):

那么如果我们既没有用户参数也没有电影特征,可以使用协同过滤算法来同时学习两者。我们的优化目标同时针对x和θ进行。
Cost Function: ![]()
Goal: 
Gradient Descent Update:

PS:在协同过滤中,通常不加bias项x0和θ0,如果需要,算法会自动获得。
练习:
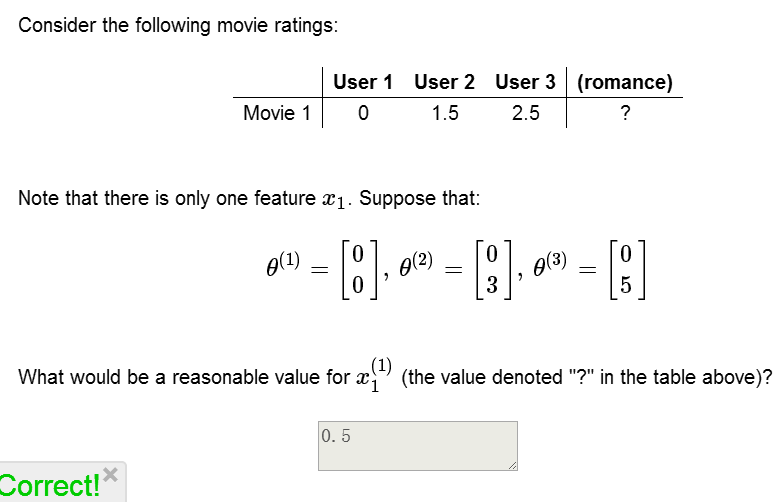

协同过滤算法步骤:
- 将x(1),x(2),...,x(nm),θ(1),θ(2),...,θ(nu)初始化为随机小值;
- 使用梯度下降法最小化cost function,训练得到θ和x;
- 对用户 j,我们预测他对电影 i 的评分为:(θ(j))T(x(i));
PS:协同过滤算法获得的特征矩阵包含了电影的相关数据,这些数据不总是人能读懂的,但我们可以用这些数据作为给用户推荐电影的依据,如一位用户看了电影 x(i),如果对于另一部电影x(j),||x(i)-x(j)||很小,我们可以为他推荐电影x(j)。
练习:


均值归一化(Mean normalization)
现在我们新增一个用户Eve,Eve没有为电影做出任何评分,那么如何为Eve推荐电影呢?
| Movie | Alica(1) | Bob(2) | Carol(3) | Dave(4) |
Eve(5) |
| Love at last | 5 | 5 | 0 | 0 | ? |
| Romance forever | 5 | ? | ? | 0 | ? |
| Cute puppies of love | ? | 4 | 0 | ? | ? |
| Nonstop car chases | 0 | 0 | 5 | 4 | ? |
| Swords vs. karate | 0 | 0 | 5 | ? |
? |
1. 首先对Y矩阵进行均值归一化,将每个用户对某个电影的评分减去所有用户对该电影的均值:

2. 利用新的Y矩阵来训练算法,再用新训练出的矩阵来预测评分,并需要将平局值加回去,即(θ(j))T(x(i))+μi。那么对于新用户Eve,模型认为他给电影的评分为每部电影的平均分,以此来进行推荐。

HOMEWORK
好了,既然看完了视频课程,就来做一下作业吧,下面是Anomaly Detection&Recommender Systems部分作业,在此仅列出核心代码:
1. estimateGaussian
mu = (sum(X)/m)'; for i =1:n sigma2(i) = sum((X(:,i)-mu(i)).^2) / (m); end
2.selectThreshold
cvPredictions = (pval < epsilon); % calculate the F1 score fp=sum((cvPredictions==1)&(yval==0)); tp=sum((cvPredictions==1)&(yval==1)); fn=sum((cvPredictions==0)&(yval==1)); prec=tp/(tp+fp); rec=tp/(tp+fn); F1=2*prec*rec/(prec+rec);
3.cofiCostFunc
%cal cost function tp = X*Theta'.*R - Y.*R; %J = sum(sum(tp.^2))/2; %unregulized J = sum(sum(tp.^2))/2 + lambda/2*sum(sum(Theta.^2)) + lambda/2*sum(sum(X.^2)); %regulized %cal grand X_grad = tp*Theta + lambda*X; Theta_grad = tp'*X + lambda*Theta;