原文链接:http://tecdat.cn/?p=19664
MCMC是从复杂概率模型中采样的通用技术。
-
蒙特卡洛
-
马尔可夫链
-
Metropolis-Hastings算法
问题
如果需要计算有复杂后验pdf p(θ| y)的随机变量θ的函数f(θ)的平均值或期望值。
![]()
您可能需要计算后验概率分布p(θ)的最大值。
![]()
解决期望值的一种方法是从p(θ)绘制N个随机样本,当N足够大时,我们可以通过以下公式逼近期望值或最大值
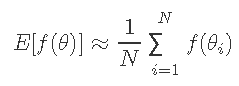
将相同的策略应用于通过从p(θ| y)采样并取样本集中的最大值来找到argmaxp(θ| y)。
解决方法
1.1直接模拟
1.2逆CDF
1.3拒绝/接受抽样
如果我们不知道精确/标准化的pdf或非常复杂,则MCMC会派上用场。
马尔可夫链
![]()
为了模拟马尔可夫链,我们必须制定一个 过渡核T(xi,xj)。过渡核是从状态xi迁移到状态xj的概率。
马尔可夫链的收敛性意味着它具有平稳分布π。马尔可夫链的统计分布是平稳的,那么它意味着分布不会随着时间的推移而改变。
Metropolis算法
对于一个Markov链是平稳的。基本上表示
处于状态x并转换为状态x'的概率必须等于处于状态x'并转换为状态x的概率
![]()
或者
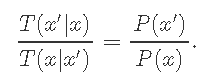
方法是将转换分为两个子步骤;候选和接受拒绝。
令q(x'| x)表示 候选密度,我们可以使用概率 α(x'| x)来调整q 。
候选分布 Q(X'| X)是给定的候选X的状态X'的条件概率,
和 接受分布 α(x'| x)的条件概率接受候选的状态X'-X'。我们设计了接受概率函数,以满足详细的平衡。
该 转移概率 可以写成:
![]()
插入上一个方程式,我们有
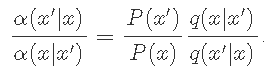
Metropolis-Hastings算法
A的选择遵循以下逻辑。
![]()
在q下从x到x'的转移太频繁了。因此,我们应该选择α(x | x')=1。但是,为了满足 细致平稳,我们有
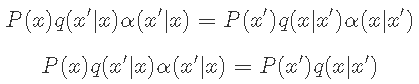
下一步是选择满足上述条件的接受。Metropolis-Hastings是一种常见的 选择:
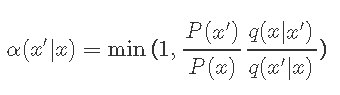
即,当接受度大于1时,我们总是接受,而当接受度小于1时,我们将相应地拒绝。因此,Metropolis-Hastings算法包含以下内容:
-
初始化:随机选择一个初始状态x;
-
根据q(x'| x)随机选择一个新状态x';
3.接受根据α(x'| x)的状态。如果不接受,则不会进行转移,因此无需更新任何内容。否则,转移为x';
4.转移到2,直到生成T状态;
5.保存状态x,执行2。
原则上,我们从分布P(x)提取保存的状态,因为步骤4保证它们是不相关的。必须根据候选分布等不同因素来选择T的值。 重要的是,尚不清楚应该使用哪种分布q(x'| x);必须针对当前的特定问题进行调整。
属性
Metropolis-Hastings算法的一个有趣特性是它 仅取决于比率
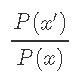
是候选样本x'与先前样本xt之间的概率,
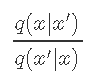
是两个方向(从xt到x',反之亦然)的候选密度之比。如果候选密度对称,则等于1。
马尔可夫链从任意初始值x0开始,并且算法运行多次迭代,直到“初始状态”被“忘记”为止。这些被丢弃的样本称为预烧(burn-in)。其余的x可接受值集代表分布P(x)中的样本
Metropolis采样
一个简单的Metropolis-Hastings采样
让我们看看从 伽玛分布 模拟任意形状和比例参数,使用具有Metropolis-Hastings采样算法。
下面给出了Metropolis-Hastings采样器的函数。该链初始化为零,并在每个阶段都建议使用N(a / b,a /(b * b))个候选对象。
![]()
基于正态分布且均值和方差相同gamma的Metropolis-Hastings独立采样
- 从某种状态开始xt。代码中的x。
- 在代码中提出一个新的状态x'候选
- 计算“接受概率”
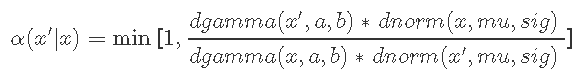
- 从[0,1] 得出一些均匀分布的随机数u;如果u <α接受该点,则设置xt + 1 = x'。否则,拒绝它并设置xt + 1 = xt。
MH可视化
-
set.seed(123)
-
-
for (i in 2:n) {
-
can <- rnorm(1, mu, sig)
-
aprob <- min(1, (dgamma(can, a, b)/dgamma(x,
-
-
-
u <- runif(1)
-
if (u < aprob)
-
x <- can
-
画图
设置参数。
-
nrep<- 54000
-
burnin<- 4000
-
shape<- 2.5
-
rate<-2.6
修改图,仅包含预烧期后的链
-
vec=vec[-(1:burnin)]
-
#vec=vec[burnin:length(vec)]
-
par(mfrow=c(2,1)) # 更改主框架,在一帧中有多少个图形
-
plot(ts(vec), xlab="Chain", ylab="Draws")
-
abline(h = mean(vec), lwd="2", col="red" )
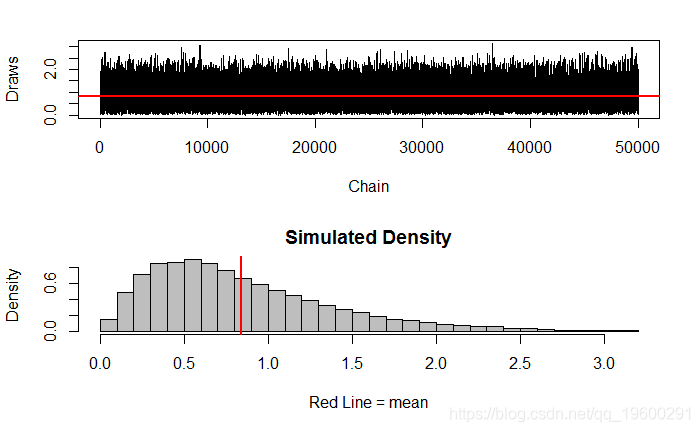
-
Min. 1st Qu. Median Mean 3rd Qu. Max.
-
0.007013 0.435600 0.724800 0.843300 1.133000 3.149000
var(vec[-(1:burnin)])[1] 0.2976507初始值
第一个样本 vec 是我们链的初始/起始值。我们可以更改它,以查看收敛是否发生了变化。
-
x <- 3*a/b
-
vec[1] <- x
选择方案
如果候选密度与目标分布P(x)的形状匹配,即q(x'| xt)≈P(x')q(x'|),则该算法效果最佳。 xt)≈P(x')。如果使用正态候选密度q,则在预烧期间必须调整方差参数σ2。
通常,这是通过计算接受率来完成的,接受率是在最后N个样本的窗口中接受的候选样本的比例。
如果σ2太大,则接受率将非常低,因为候选可能落在概率密度低得多的区域中,因此a1将非常小,且链将收敛得非常慢。
示例2:回归的贝叶斯估计
Metropolis-Hastings采样用于贝叶斯估计回归模型。
设定参数
DGP和图
-
# 创建独立的x值,大约为零
-
x <- (-(Size-1)/2):((Size-1)/2)
-
# 根据ax + b + N(0,sd)创建相关值
-
y <- trueA * x + trueB + rnorm(n=Size,mean=0,sd=trueSd)
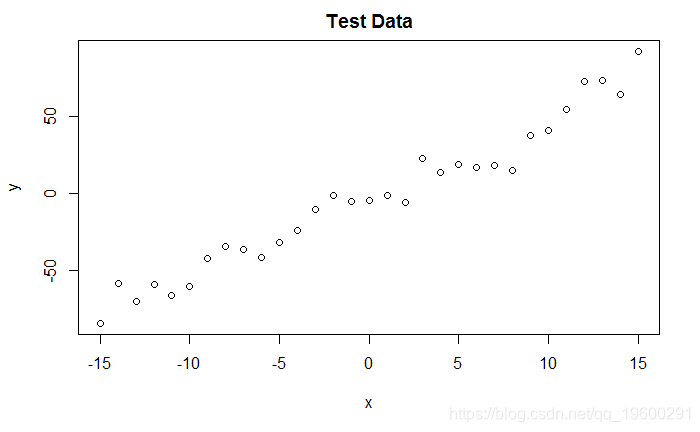
正态分布拟然
-
-
pred = a*x + b
-
singlelikelihoods = dnorm(y, mean = pred, sd = sd, log = T)
-
sumll = sum(singlelikelihoods)
为什么使用对数
似然函数中概率的对数,这也是我求和所有数据点的概率(乘积的对数等于对数之和)的原因。
我们为什么要做这个?强烈建议这样做,因为许多小概率相乘的概率会变得很小。在某个阶段,计算机程序会陷入数值四舍五入或下溢问题。
因此, 当您编写概率时,请始终使用对数
示例:绘制斜率a的似然曲线
-
# 示例:绘制斜率a的似然曲线
-
plot (seq(3, 7, by=.05), slopelikelihoods , type="l")

先验分布
这三个参数的均匀分布和正态分布。
-
# 先验分布
-
-
# 更改优先级,log为True,因此这些均为log
-
density/likelihood
-
aprior = dunif(a, min=0, max=10, log = T)
-
bprior = dnorm(b, sd = 2, log = T)
-
sdprior = dunif(sd, min=0, max=30, log = T)
后验
先验和概率的乘积是MCMC将要处理的实际量。此函数称为后验函数。同样,这里我们使用和,因为我们使用对数。
-
posterior <- function(param){
-
return (likelihood(param) + prior(param))
-
}
Metropolis算法
该算法是从 后验密度中采样最常见的贝叶斯统计应用之一 。
上面定义的后验。
-
从随机参数值开始
-
根据某个候选函数的概率密度,选择一个接近旧值的新参数值
-
以概率p(new)/ p(old)跳到这个新点,其中p是目标函数,并且p> 1也意味着跳跃
-
请注意,我们有一个 对称的跳跃/候选分布 q(x'| x)。
![]()
标准差σ是固定的。![]()
所以接受概率等于
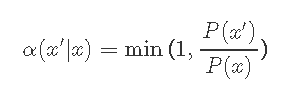
-
######## Metropolis 算法 ################
-
-
-
for (i in 1:iterations){
-
-
probab = exp(posterior(proposal) - posterior(chain[i,]))
-
if (runif(1) < probab){
-
-
}else{
-
-
}
实施
(e)输出接受的值,并解释。
-
-
chain = metrMCMC(startvalue, 5500)
-
-
burnIn = 5000
-
accep = 1-mean(duplicated(chain[-(1:burnIn),]))
算法的第一步可能会因初始值而有偏差,因此通常会被丢弃来进行进一步分析(预烧期)。令人感兴趣的输出是接受率:候选多久被算法接受拒绝一次?候选函数会影响接受率:通常,候选越接近,接受率就越大。但是,非常高的接受率通常是无益的:这意味着算法在同一点上“停留”,这导致对参数空间(混合)的处理不够理想。
我们还可以更改初始值,以查看其是否更改结果/是否收敛。
startvalue = c(4,0,10)小结
-
V1 V2 V3
-
Min. :4.068 Min. :-6.7072 Min. : 6.787
-
1st Qu.:4.913 1st Qu.:-2.6973 1st Qu.: 9.323
-
Median :5.052 Median :-1.7551 Median :10.178
-
Mean :5.052 Mean :-1.7377 Mean :10.385
-
3rd Qu.:5.193 3rd Qu.:-0.8134 3rd Qu.:11.166
-
Max. :5.989 Max. : 4.8425 Max. :19.223
-
#比较:
-
summary(lm(y~x))
-
-
Call:
-
lm(formula = y ~ x)
-
-
Residuals:
-
Min 1Q Median 3Q Max
-
-22.259 -6.032 -1.718 6.955 19.892
-
-
Coefficients:
-
Estimate Std. Error t value Pr(>|t|)
-
(Intercept) -3.1756 1.7566 -1.808 0.081 .
-
x 5.0469 0.1964 25.697 <2e-16 ***
-
-
Signif. codes: 0 ?**?0.001 ?*?0.01 ??0.05 ??0.1 ??1
-
-
Residual standard error: 9.78 on 29 degrees of freedom
-
Multiple R-squared: 0.9579, Adjusted R-squared: 0.9565
-
F-statistic: 660.4 on 1 and 29 DF, p-value: < 2.2e-16
summary(lm(y~x))$sigma[1] 9.780494coefficients(lm(y~x))[1]-
(Intercept)
-
-3.175555
coefficients(lm(y~x))[2]-
x
-
5.046873
总结:
-
### 总结: #######################
-
-
par(mfrow = c(2,3))
-
hist(chain[-(1:burnIn),1],prob=TRUE,nclass=30,col="109"
-
abline(v = mean(chain[-(1:burnIn),1]), lwd="2")


最受欢迎的见解