拓端数据tecdat|Matlab中的偏最小二乘法（PLS）回归模型，离群点检测和变量选择

原文 | http://tecdat.cn/?p=22319 
来源 | 拓端数据部落公众号
 

本文建立偏最小二乘法（PLS）回归（PLSR）模型，以及预测性能评估。为了建立一个可靠的模型，我们还实现了一些常用的离群点检测和变量选择方法，可以去除潜在的离群点和只使用所选变量的子集来 "清洗 "你的数据。

步骤

• 建立PLS回归模型
• PLS的K-折交叉验证
• PLS的蒙特卡洛交叉验证（MCCV）。
• PLS的双重交叉验证(DCV)
• 使用蒙特卡洛抽样方法进行离群点检测
• 使用CARS方法进行变量选择。
• 使用移动窗口PLS（MWPLS）进行变量选择。
• 使用蒙特卡洛无信息变量消除法（MCUVE）进行变量选择
• 进行变量选择

建立PLS回归模型

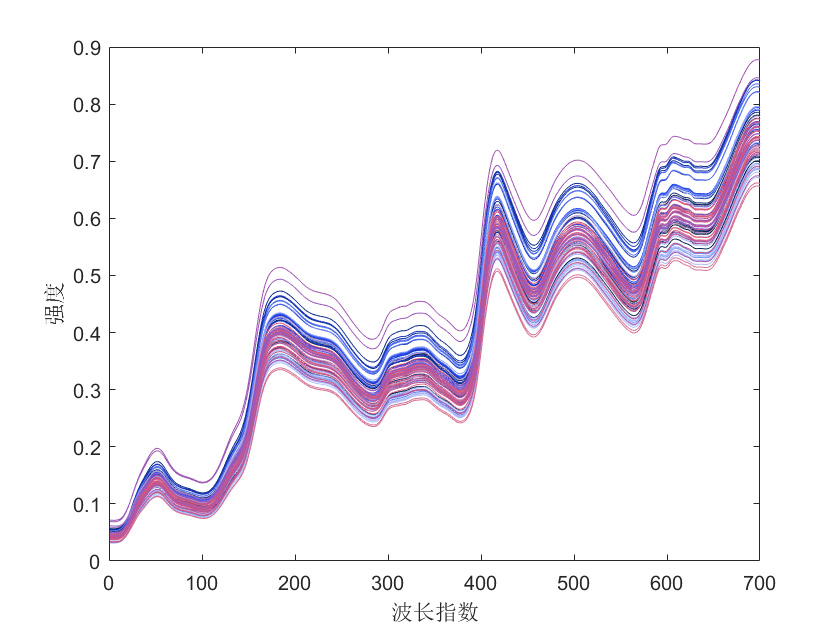
这个例子说明了如何使用基准近红外数据建立PLS模型。

1.  
    
2.  
   plot(X'); % 显示光谱数据。
3.  
   xlabel('波长指数');
4.  
   ylabel('强度');

参数设定

1.  
    
2.  
   A=6; % 潜在变量（LV）的数量。
3.  
   method='center'; % 用于建立PLS模型的X的内部预处理方法
4.  
   PLS(X,y,A,method); % 建立模型的命令

 

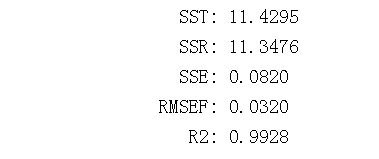
pls.m函数返回一个包含成分列表的对象PLS。结果解释。

regcoef_original：连接X和y的回归系数。
X_scores：X的得分。
VIP：预测中的变量重要性，评估变量重要性的一个标准。
变量的重要性。
RMSEF：拟合的均方根误差。
y_fit：y的拟合值。
R2：Y的解释变异的百分比。 

PLS的K折交叉验证

说明如何对PLS模型进行K折交叉验证

1.  
   clear;
2.  
   A=6; % LV的数量
3.  
   K=5; % 交叉验证的次数

1.  
    
2.  
   plot(CV.RMSECV) % 绘制每个潜在变量(LVs)数量下的RMSECV值
3.  
   xlabel('潜在变量(LVs)数量') % 添加x标签
4.  
   ylabel('RMSECV') % 添加y标签

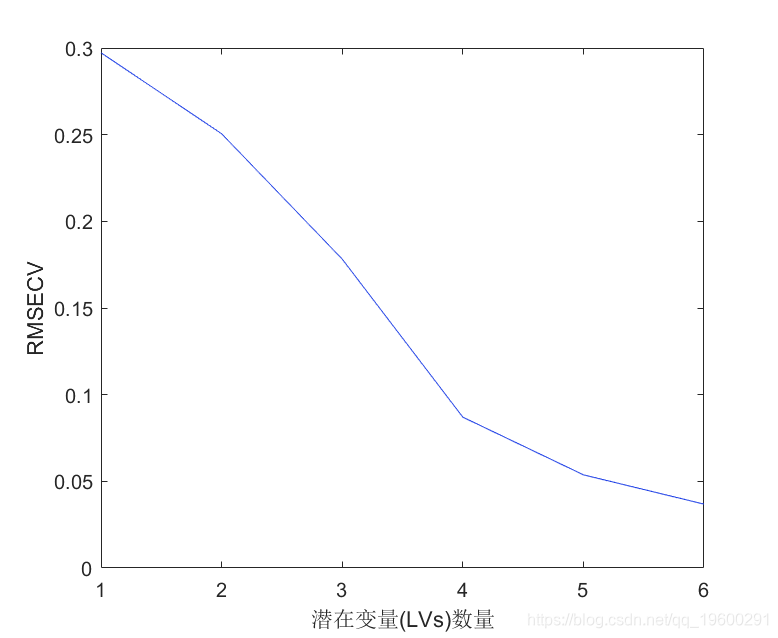
返回的值CV是带有成分列表的结构数据。结果解释。

RMSECV：交叉验证的均方根误差。越小越好
Q2：与R2含义相同，但由交叉验证计算得出。
optLV：达到最小RMSECV（最高Q2）的LV数量。 

蒙特卡洛交叉验证（MCCV）的PLS

说明如何对PLS建模进行MCCV。与K-fold CV一样，MCCV是另一种交叉验证的方法。

1.  
   % 参数设置
2.  
   A=6;
3.  
   method='center';
4.  
   N=500; % Monte Carlo抽样的数量
5.  
   % 运行mccv.
6.  
   plot(MCCV.RMSECV); % 绘制每个潜在变量(LVs)数量下的RMSECV值
7.  
   xlabel('潜在变量(LVs)数量');

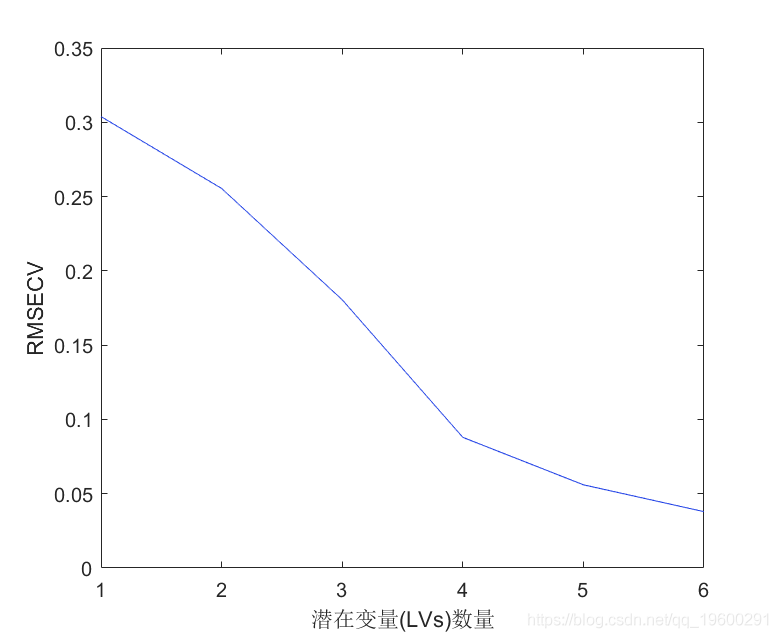
MCCV

MCCV是一个结构性数据。结果解释。

Ypred:预测值
Ytrue：真实值
RMSECV：交叉验证的均方根误差，越小越好。
Q2：与R2含义相同，但由交叉验证计算得出。 

PLS的双重交叉验证（DCV）

说明如何对PLS建模进行DCV。与K-fold CV一样，DCV是交叉验证的一种方式。

1.  
    
2.  
   % 参数设置
3.  
    
4.  
   N=50; % Monte Carlo抽样的数量
5.  
   dcv(X,y,A,k,method,N);
6.  
   DCV

使用蒙特卡洛抽样方法的离群点检测

说明离群点检测方法的使用情况

1.  
   A=6;
2.  
   method='center';
3.  
   F=mc(X,y,A,method,N,ratio);
4.  
    

结果解释。

predError：每个抽样中的样本预测误差
MEAN：每个样本的平均预测误差
STD:每个样本的预测误差的标准偏差 

plot(F) % 诊断图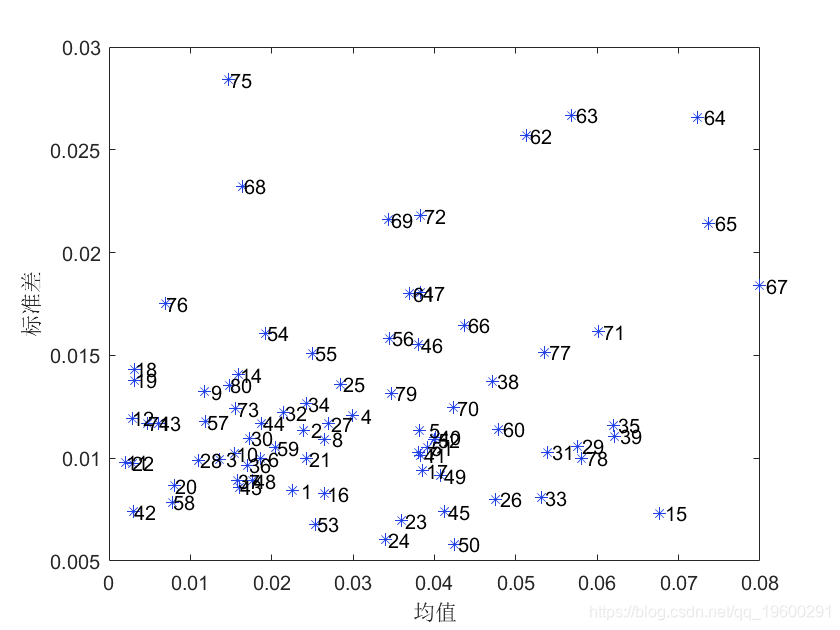

注：MEAN值高或SD值高的样本更可能是离群值，应考虑在建模前将其剔除。

使用CARS方法进行变量选择。

1.  
    
2.  
   A=6;
3.  
   fold=5;
4.  
   car(X,y,A,fold);
5.  
    

结果解释。

optLV:最佳模型的LV数量
vsel:选定的变量（X中的列）。 

plotcars(CARS); % 诊断图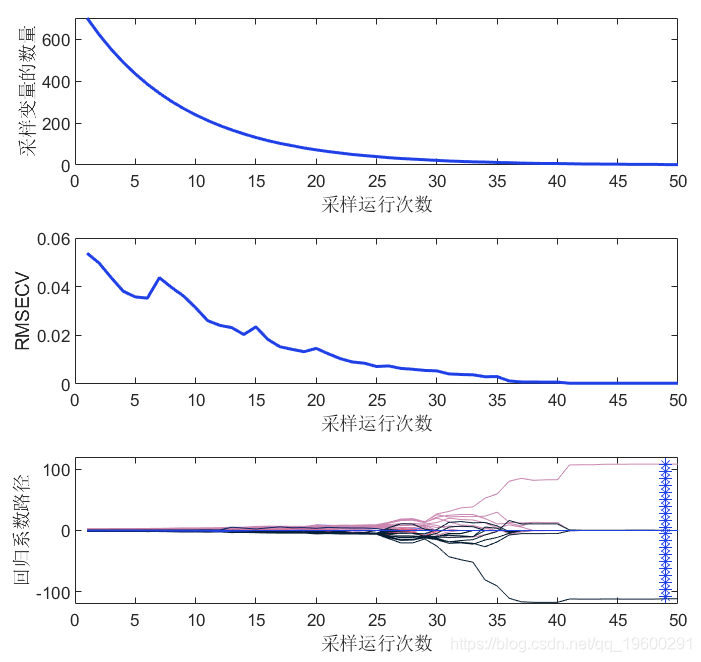

注：在这幅图中，顶部和中间的面板显示了选择变量的数量和RMSECV如何随着迭代而变化。底部面板描述了每个变量的回归系数（每条线对应一个变量）如何随着迭代而变化。星形垂直线表示具有最低RMSECV的最佳模型。

使用移动窗口PLS（MWPLS）进行变量选择

1.  
   load corn_m51; % 示例数据
2.  
   width=15; % 窗口大小
3.  
   mw(X,y,width);
4.  
   plot(WP,RMSEF);
5.  
   xlabel('窗口位置');

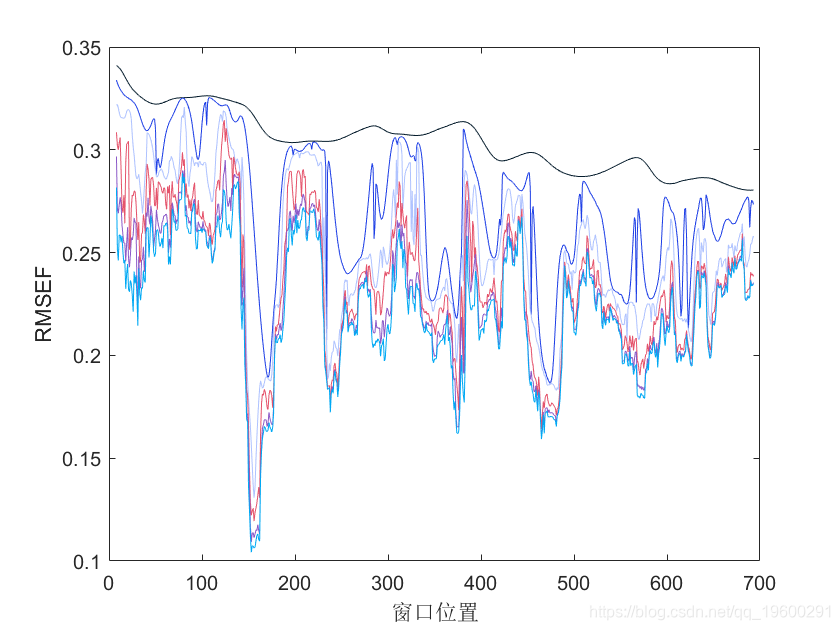
注：从该图中建议将RMSEF值较低的区域纳入PLS模型中。

使用蒙特卡洛无信息变量消除法（MCUVE）进行变量选择

1.  
   N=500;
2.  
   method='center';
3.  
    
4.  
   UVE

1.  
    
2.  
   plot(abs(UVE.RI))

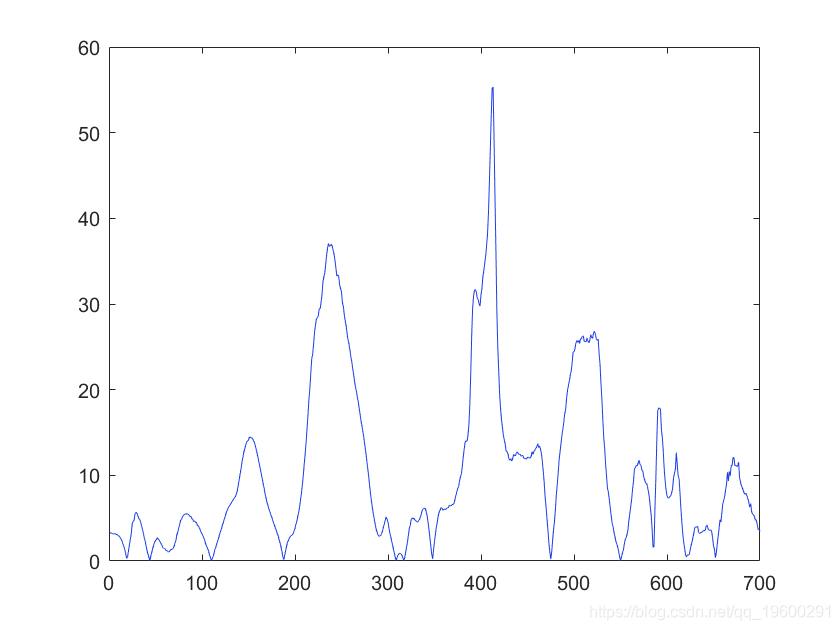
结果解释。RI：UVE的可靠性指数，是对变量重要性的测量，越高越好。

进行变量选择

1.  
   A=6;
2.  
   N=10000;
3.  
   method='center';
4.  
   FROG=rd_pls(X,y,A,method,N);
5.  
    
6.  
    
7.  
   N: 10000
8.  
   Q: 2
9.  
   model: [10000x700 double]
10.  
    minutes: 0.6683
11.  
    method: 'center'
12.  
    Vrank: [1x700 double]
13.  
    Vtop10: [505 405 506 400 408 233 235 249 248 515]
14.  
    probability: [1x700 double]
15.  
    nVar: [1x10000 double]
16.  
    RMSEP: [1x10000 double]
17.  
     

1.  
    
2.  
   xlabel('变量序号');
3.  
   ylabel('选择概率'); 

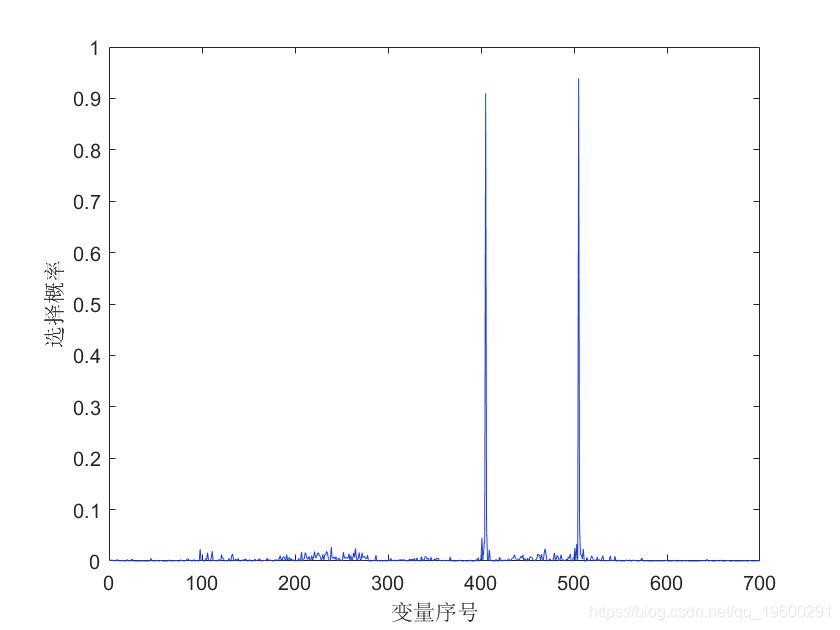
结果解释：

模型结果是一个矩阵，储存了每一个相互关系中的选择变量。
概率：每个变量被包含在最终模型中的概率。越大越好。这是一个衡量变量重要性的有用指标。

---

最受欢迎的见解

1.R语言多元Logistic逻辑回归 应用案例

2.面板平滑转移回归(PSTR)分析案例实现

3.matlab中的偏最小二乘回归（PLSR）和主成分回归（PCR）

4.R语言泊松Poisson回归模型分析案例

5.R语言回归中的Hosmer-Lemeshow拟合优度检验

6.r语言中对LASSO回归，Ridge岭回归和Elastic Net模型实现

7.在R语言中实现Logistic逻辑回归

8.python用线性回归预测股票价格

9.R语言如何在生存分析与Cox回归中计算IDI，NRI指标