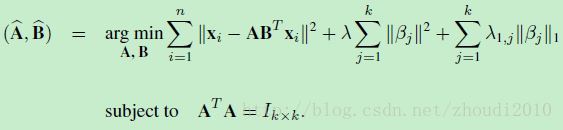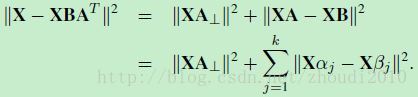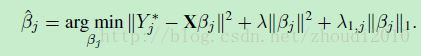Sparse PCA 稀疏主成分分析
SPCA原始文献:H. Zou (2006) Sparse principal component analysis
PCA 可以参考: The Elements of Statistical Learning 第十四章
主成分分析的基本思想以及R的应用可以参考:稀疏主成分分析与R应用
关于统计学习中的稀疏算法可以参考:Statistical learning with sparsity: the lasso and generalizations
一份很好的文档:http://www.cs.utexas.edu/~rashish/sparse_pca.pdf
首先直接来看算法:
- 令A初始化为V[,1:k],即为前k个principal components的loading vectors.
- 对于给定的A=[α1,…,αk]A=[α1,…,αk] , 优化elastic net:
βj=argmaxβ(αi−β)TXTX(αi−β)+λ∥β∥2+λ1,j∥β∥1βj=argmaxβ(αi−β)TXTX(αi−β)+λ‖β‖2+λ1,j‖β‖1 - 对于给定的B=[β1,…,βk]B=[β1,…,βk], 计算XTXBXTXB的SVD,更新A=UVTA=UVT.
- 重复2-3步,直到收敛.
- Normalization之后得到ViVi
接下来对该算法进行必要的解释:
想要得到稀疏的结果,核心思想是在优化参数时加入 L1L1 penalty. 另外,如果我们将PCA问题转化为regression问题,那么就达到了求解稀疏主成分的目的了。
H. Zou (2006)的Theorem 1就提出了PCA和Regression的联系。即:如果我们已经知道由SVD得到的principal components, 那么ridge estimates就是ViVi.
βridge=argmaxβ∥Zi−Xβ∥2+λ∥β∥2βridge=argmaxβ‖Zi−Xβ‖2+λ‖β‖2
如果在上式中加入L1L1 penalty: λ1∥β∥1λ1‖β‖1,那么就可以得到了sparse PCs. 但是这是一个仍然依赖PCA的结果,我们想要得到一个self-contained的方法。
所以新的优化问题是这样的形式:
第二项和第三项是elastic net,或者理解为ridge+lasso. 第一项则和之前的形式有些不同。如果我们令A=BA=B,那么第一项就变成了∥xi−AATxi∥2‖xi−AATxi‖2, 这个形式就是PCA的形式(注释1).
这一步我们遇到的问题是:
1. AA 和 BB 我们都不知道,如果同时优化,能量方程并不是凸优化问题,但固定其中一个变量,则为凸优化问题。
2. ∥xi−ABTxi∥2‖xi−ABTxi‖2 形式不方便elastic net优化
解决思路是:
1. 将问题转化为:如果AA已知,求BB;然后根据求得的BB,求AA,如此迭代。
2. 将∥xi−ABTxi∥2‖xi−ABTxi‖2 形式转化为∥Y−XTβ∥2‖Y−XTβ‖2 形式。
先说问题2的解决方法(注释2):
令Y∗=XαjY∗=Xαj
就得到了最终需要的形式:
再说问题1的算法,也就是文章最开始提到的算法中的2,3步(注释3):
如此这般,SPCA就ok了!
不过,还有几个小问题:
注释1处 为什么A=BA=B就退化成了PCA?
具体可以参考The Elements of Statistical Learning 14.5
我们为了最小化reconstruction error:
∥xi−μ−Vqλi∥2‖xi−μ−Vqλi‖2
得到 λ^i=V⊤q(xi−x¯)λ^i=Vq⊤(xi−x¯)
将其带入error,可以得到orthogonal matrix VqVq使其最小化:
∥(xi−x¯)−VqV⊤q(xi−x¯)∥2‖(xi−x¯)−VqVq⊤(xi−x¯)‖2
VqV⊤qVqVq⊤就是projection matrix.
所以A=BA=B,AA就相当于VV.
注释2处 这个转化怎么得到的?
∥X−XBA⊤∥2‖X−XBA⊤‖2 = ∥XA⊥∥2‖XA⊥‖2 + ∥XA−XB∥2‖XA−XB‖2
注意到AA为orthonomal,A⊥A⊥也是orthonomal matrix并且使得[A;A⊥][A;A⊥]是p×pp×p orthonomal matrix.
所以将 ∥X−XBA⊤∥2‖X−XBA⊤‖2 投影到AA 和A⊥A⊥可以得到 :
∥X−XBA⊤∥2‖X−XBA⊤‖2
= ∥(X−XBA⊤)A⊥∥2‖(X−XBA⊤)A⊥‖2 + ∥(X−XBA⊤)A∥2‖(X−XBA⊤)A‖2
= ∥XA⊥∥2‖XA⊥‖2 +∥XA−XB∥2‖XA−XB‖2
注释3处 A given B 怎么证明?
需要用到Procrustes Rotation的结论:
(A.7)是squared Frobenius matrix norm, 所以 ∥X∥2=trace(X⊤X)‖X‖2=trace(X⊤X).
Procrustes (普洛克路斯忒斯)是希腊神话中的一名强盗。他是海神波塞冬的儿子,在从雅典到埃莱夫西纳的路上开设黑店,拦截行人。店内设有一张铁床,旅客投宿时,将身高者截断,身矮者则强行拉长,使与床的长短相等。而由于普洛克路斯忒斯秘密地拥有两张长度不同的床,所以无人能因身高恰好与床相等而幸免。后来英雄忒修斯前往雅典时,路过此地,将其杀死。(From Wiki)