300. 最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
O(N^2) O(N)
class Solution { public int lengthOfLIS(int[] nums) { //dp[i] 前i个元素组成的最长上升子序列的长度(必须包含nums[i]) int len =0,n =nums.length; int dp[] =new int[n+1]; dp[len] =1; int maxx =1; for(int i=1;i<n;i++){ dp[i] =1; for(int j=0;j<i;j++ ){ if(nums[i]>nums[j]){ dp[i] =Math.max(dp[i],dp[j]+1); maxx =Math.max(maxx,dp[i]); } } } return maxx; } }
class Solution { public int lengthOfLIS(int[] nums) { //希望递增子序列更长,表示该序列增加的更缓慢。也就是希望一定长度下的递增子序列的最后一个值更小 //dp[l]: 长度为l的递增子序列的末尾最小值 //0 2 1 7 :0 2 ,0 1,0 7,2 7 dp[2]=1 //因此dp 递增,可以二分 int n = nums.length; int dp[] =new int [n+1]; int l=1; dp[l] = nums[0]; for(int i =1;i<n;i++){ if(nums[i]>dp[l]){ dp[++l] =nums[i]; } else{ int j=1,k=l,pos=0; while(j<=k){ int mid =(j+k)>>1; //在dp[1-l]中找到第一个比nums[i]大的数 if(nums[i]>dp[mid]){//只要小于nums[i]就记录 pos =mid; j =mid+1; } else{ k =mid-1; } } //pos+1就是dp[1-l]中找到第一个比nums[i]大的数的ID dp[pos+1]=nums[i]; } } return l; } }
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
示例 1:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物
提示:
0 < grid.length <= 200
0 < grid[0].length <= 200
//DP
//grid[i][j] 以[i][j]为右下角的棋盘结果(礼物最大值) class Solution { public int maxValue(int[][] grid) { for(int i =0;i<grid.length;i++){ for(int j =0;j<grid[0].length;j++){ if(i==0&&j==0) continue; else if(i==0) grid[i][j]+=grid[i][j-1];//只能从左边过来 else if(j==0) grid[i][j]+=grid[i-1][j]; else grid[i][j]+=Math.max(grid[i-1][j],grid[i][j-1]); } } return grid[grid.length-1][grid[0].length-1]; } }
//DFS
class Solution { int m,n; public int maxValue(int[][] grid) { this.m = grid.length; this.n =grid[0].length; int [][]men =new int[m][n];//mem[i][j]从右下角到(i,j)的礼物最大值 return dfs(grid,men,0,0,1); } public int dfs(int [][]grid,int [][]mem,int x,int y,int num){ if(x>=m||y>=n) return 0; if(mem[x][y]!=0) return mem[x][y];//走过的不要重复,走过的一定是最优解了 if(num==m+n) return 0;//回溯 int down = dfs(grid,mem,x+1,y,num+1); int right = dfs(grid,mem,x,y+1,num+1); int ans =grid[x][y]+Math.max(down,right); mem[x][y] =ans; return ans; } }
剑指 Offer 49. 丑数
我们把只包含质因子 2、3 和 5 的数称作丑数(Ugly Number)。求按从小到大的顺序的第 n 个丑数。
思路参考:https://leetcode-cn.com/problems/chou-shu-lcof/solution/mian-shi-ti-49-chou-shu-dong-tai-gui-hua-qing-xi-t/
class Solution { public int nthUglyNumber(int n) { int []dp =new int[n+1]; dp[1]=1; int a=1,b=1,c=1; int num1,num2,num3; for(int i =2;i<=n;i++){ numa = dp[a]*2; numb = dp[b]*3; numc = dp[c]*5; dp[i] =Math.min(num1,Math.min(num2,num3)); if(dp[i]==numa) a++;//第i个丑数是第a个丑数乘以2得到的,因此需要用第a+1个丑数乘以2来作为第i+1个丑数的可选项。 //如果第i个丑数不是第a个丑数乘以2得到的,那么a不变 if(dp[i]==numb) b++; if(dp[i]==numc) c++; } return dp[n]; } }
编辑距离
给你两个单词 word1 和 word2,请你计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
示例1
"abc","adc",5,3,2
2
示例2
"abc","adc",5,3,100
......i
class Solution { public int minDistance(String word1, String word2) { word1 = " "+word1; word2 =" "+word2; int t =1; int l1=word1.length(),l2 =word2.length(); // System.out.println(l1+" "+l2); int dp[][] =new int[l1][l2]; for(int i =0;i<l1;i++) dp[i][0] =i;//删除 for(int i=0;i<l2;i++) dp[0][i] =i;//添加 for(int i =1;i<l1;i++) { for(int j =1;j<l2;j++){ dp[i][j] =Math.min(dp[i-1][j],dp[i][j-1])+1; if(word1.charAt(i)==word2.charAt(j)){ t =0; } dp[i][j] =Math.min(dp[i][j],dp[i-1][j-1]+t); t =1; } } return dp[l1-1][l2-1]; } }
描述
import java.util.*; public class Solution { /** * min edit cost * @param str1 string字符串 the string * @param str2 string字符串 the string * @param ic int整型 insert cost * @param dc int整型 delete cost * @param rc int整型 replace cost * @return int整型 */ public int minEditCost (String str1, String str2, int ic, int dc, int rc) { str1 = " "+str1; str2 =" "+str2; int t =0; int l1=str1.length(),l2 =str2.length(); int dp[][] =new int[l1][l2]; for(int i =0;i<l1;i++) dp[i][0] =i*dc;//删除 for(int i=0;i<l2;i++) dp[0][i] =i*ic;//插入 for(int i =1;i<l1;i++) { for(int j =1;j<l2;j++){ dp[i][j] =Math.min(dp[i-1][j]+dc,dp[i][j-1]+ic); if(str1.charAt(i)!=str2.charAt(j)){ t =rc; } dp[i][j] =Math.min(dp[i][j],dp[i-1][j-1]+t); t =0; } } return dp[l1-1][l2-1]; } }
滚动数组优化空间复杂度
import java.util.*; public class Solution { /** * min edit cost * @param str1 string字符串 the string * @param str2 string字符串 the string * @param ic int整型 insert cost * @param dc int整型 delete cost * @param rc int整型 replace cost * @return int整型 */ public int minEditCost (String str1, String str2, int ic, int dc, int rc) { str1 = " "+str1; char s1 [] =str1.toCharArray(); str2 =" "+str2; char s2 [] =str2.toCharArray(); int t =0; int l1=s1.length,l2 =s2.length; int dp[] =new int[l2]; // for(int i =0;i<l1;i++) dp[i][0] =i*dc;//删除 for(int i=0;i<l2;i++) dp[i] =i*ic;//插入 int pre,tmp; for(int i =1;i<l1;i++) { pre =dp[0];//dp[i-1][0] dp[0] = i*dc;//dp[i][0] for(int j =1;j<l2;j++){ tmp =dp[j];//dp[i-1][j] // dp[i][j] =Math.min(dp[i-1][j]+dc,dp[i][j-1]+ic); dp[j] =Math.min(tmp+dc,dp[j-1]+ic);//dp[j-1]:dp[i][j-1] if(str1.charAt(i)!=str2.charAt(j)){ t =rc; } //dp[i][j] =Math.min(dp[i][j],dp[i-1][j-1]+t); dp[j] =Math.min(dp[j],pre+t); t =0; pre = tmp;//pre :对于下个j来说就是dp[i-1][j-1] } } return dp[l2-1]; } }
请从字符串中找出一个最长的不包含重复字符的子字符串,计算该最长子字符串的长度。
输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
// dp[j]:以s[j]结尾的最长的不包含重复字符的子串长度 // j:当前id, i距离s[j]最近的字符(s[i]==s[j]) // 1.i<0 表示前面没有和s[j]一样的字符 // 2.dp[j-1]>=j-i 表示i在dp[j-1]的字符串内部 // i j-1 j // p s a p a // 那么dp[j] = j-i // 3.dp[j-1]<j-i 表示i在dp[j-1]的字符串外部 // i j-1 j // a p s p a // 那么dp[j] =dp[j-1]+1 优化空间复杂度 tmp :dp[] class Solution { public int lengthOfLongestSubstring(String s) { Map<Character,Integer>map = new HashMap(); int tmp =0,maxx=0; int n =s.length(); for(int j=0;j<n;j++){ int i = map.getOrDefault(s.charAt(j),-1);// s[i]==s[j]i距离j最近 map.put(s.charAt(j),j); tmp =tmp <j-i?tmp+1:j-i; maxx =Math.max(maxx,tmp); } return maxx; } }
面试题19. 正则表达式匹配
请实现一个函数用来匹配包含'. '和'*'的正则表达式。模式中的字符'.'表示任意一个字符,而'*'表示它前面的字符可以出现任意次(含0次)。在本题中,匹配是指字符串的所有字符匹配整个模式。例如,字符串"aaa"与模式"a.a"和"ab*ac*a"匹配,但与"aa.a"和"ab*a"均不匹配。
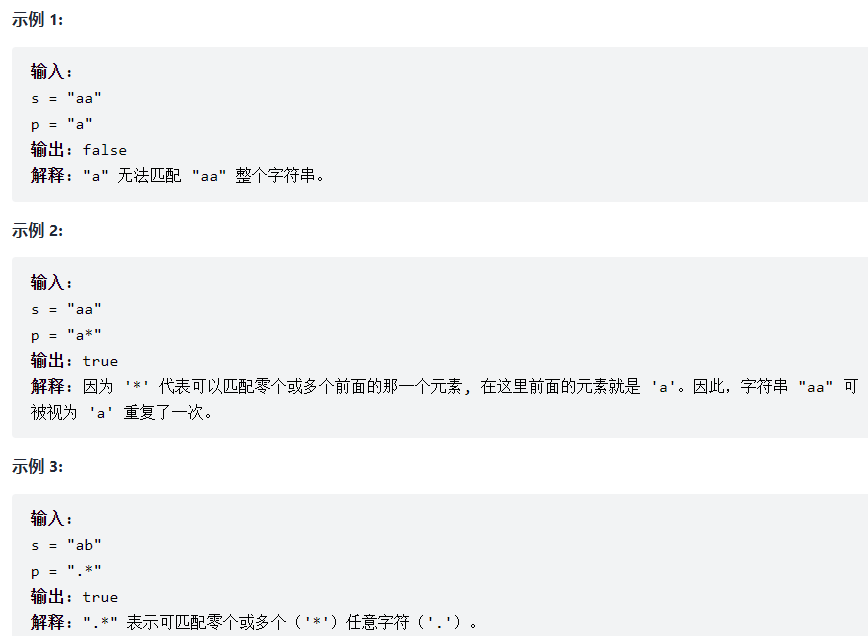
s可能为空,且只包含从a-z的小写字母。p可能为空,且只包含从a-z的小写字母以及字符.和*,无连续的'*'。
class Solution { public boolean isMatch(String s, String p) { int ls =s.length(),lp =p.length(); boolean dp[][] =new boolean[ls+1][lp+1];//dp[i][j] 表示p的前j个字符和s的前i个字符是否匹配 // 从后往前 // p的每个字符可能有三种情况:(1)正常字符,(2)'.',(3)'*' // (1)+(2) // 如果 s[i-1]==p[j-1] ||p[j-1]=='.' // dp[i][j] = dp[i-1][j-1];(i>=1&&j>=1) // (3) // 前面字符可以重复0次或者多次 // 1. 0次 // dp[i][j]|=dp[i][j-2]; (j>=2) // 2. 多次 // 如果 s[i-1]==p[j-2]||p[j-2]=='.' // dp[i][j]|=dp[i-1][j]; (i>=1&&j>=2) // (3)用的是| 表示情况1和情况2都不行才表明当前不成立 // 初始条件:dp[0][0]=1 ,dp[i][0]=0(i>0) for(int i=0;i<=ls;i++){ for(int j=0;j<=lp;j++){ if(j==0) dp[i][j]= i==0; else{ if(p.charAt(j-1)!='*'){ if(i>=1&&(s.charAt(i-1)==p.charAt(j-1)||p.charAt(j-1)=='.')){ dp[i][j] = dp[i-1][j-1]; } } else{ //两个if, 先不用c* ,再用c* // 0|0 ==0 其他都是1 if(j>=2) { dp[i][j]|=dp[i][j-2]; } if(i>=1&&j>=2&&(s.charAt(i-1)==p.charAt(j-2)||p.charAt(j-2)=='.')){ dp[i][j]|=dp[i-1][j]; } } } } } return dp[ls][lp]; } }
312. 戳气球
有 n 个气球,编号为0 到 n - 1,每个气球上都标有一个数字,这些数字存在数组 nums 中。
现在要求你戳破所有的气球。戳破第 i 个气球,你可以获得 nums[i - 1] * nums[i] * nums[i + 1] 枚硬币。 这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的序号。如果 i - 1或 i + 1 超出了数组的边界,那么就当它是一个数字为 1 的气球。
求所能获得硬币的最大数量。
题解
题目是一个个的删除元素,但是一旦删除某个元素,便直接影响元素的相对位置
因此,一个个的加元素 逆操作
3 2 5 --> 1 3 2 5 1
按照 3 2 5 的顺序删除,也就是按照 5 2 3 的顺序添加
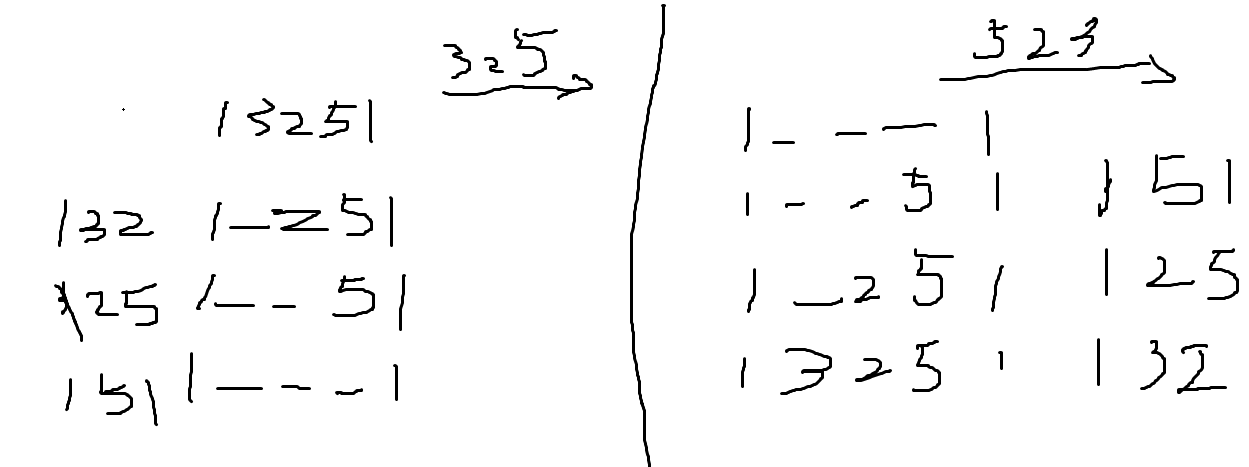
solve(i,j) 开区间 把区间(i,j)填完得到的硬币最大值
class Solution { int val[] ; int ans[][] ; public int maxCoins(int[] nums) { int n = nums.length; val=new int[n+2]; ans=new int[n+2][n+2]; for(int i=1;i<n+1;i++) val[i] =nums[i-1]; val[0]=val[n+1]=1; for(int i=0;i<n+2;i++) Arrays.fill(ans[i],-1); return solve(0,n+1); } public int solve(int left,int right){ if(left>=right-1) return 0; if(ans[left][right]!=-1) return ans[left][right];//记忆化 for(int i=left+1;i<right;i++) { int sum =val[left]*val[i]*val[right]; sum+=solve(left,i)+solve(i,right); ans[left][right] =Math.max(ans[left][right],sum); } return ans[left][right]; } }
时间复杂度 O(N^3)
空间复杂度 O(N^2)
class Solution { int val[] ; int ans[][] ; public int maxCoins(int[] nums) { int n = nums.length; val=new int[n+2]; ans=new int[n+2][n+2]; for(int i=1;i<n+1;i++) val[i] =nums[i-1]; val[0]=val[n+1]=1; for(int i=n-1;i>=0;i--){//逆序 for(int j=i+2;j<n+2;j++){ for(int k=i+1;k<j;k++){ int sum = val[i]*val[k]*val[j]; sum+=ans[i][k]+ans[k][j]; ans[i][j] = Math.max(ans[i][j],sum); } } } return ans[0][n+1]; } }
42. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

i位置处的雨水:min(i左侧最大高度,i右侧最大高度)-height[i]
暴力
O(N^2) O(1)
class Solution { public int trap(int[] height) { int n = height.length; int a[] = new int[n+1]; int maxx1=0,maxx2=0; int sum =0; for(int i=1;i<n-1;i++){ for(int j=0;j<i;j++) { if(maxx1<height[j]) maxx1 =height[j]; } for(int k=i+1;k<n;k++) { if(maxx2<height[k]) maxx2=height[k]; } int p =Math.min(maxx1,maxx2)-height[i]; sum+=p>0?p:0; maxx1=0;maxx2=0; } return sum; } }
Dp
O(N)O(N)
class Solution { public int trap(int[] height) { int n =height.length; int dp1[] =new int[n+1]; int dp2[] =new int[n+1]; for(int i=1;i<=n-2;i++){ if(height[i-1]>dp1[i]) dp1[i] = height[i-1]; if(dp1[i-1]>dp1[i]) dp1[i] =dp1[i-1]; } for(int i=n-2;i>=1;i--){ if(height[i+1]>dp2[i]) dp2[i] =height[i+1]; if(dp2[i+1]>dp2[i]) dp2[i] =dp2[i+1]; } int sum=0; for(int i=1;i<=n-2;i++){ int p =Math.min(dp1[i],dp2[i])-height[i]; sum+=p>0?p:0; } return sum; } }
双指针
O(N)O(1)
class Solution { public int trap(int[] height) { int n =height.length; int l=0,r=n-1; int sum=0; int lmax=0,rmax=0; // iL i维护lmax iR i维护rmax // jL j维护lmax jR j维护rmax // 如果j>i 肯定 iL<=jL ,iR>=jR // == 两边都可以 不影响指针移动 所以我们只分析不等的情况 // 如果 height[i]<height[j] //i++时,j不变 height[j]就是jR // (1)i++导致,j在i++的阶段保持不变。因此当前i之前不可能存在大于height[j]的数,又因为height[j]就是jR // 因此 jR>iL -->iR>iL -->i处加雨水 // (2)j++导致,i在j++的阶段保持不变。height[j]是j右边最大的数,height[j]是jR.又因为height[i]就是iL // 因此 jR>iL -->iR>iL -->i处加雨水 // height[j]<height[i] 同理 while(l<r){ if(height[l]<=height[r]) {//==放在if 和else 都可以 if(lmax<height[l]) lmax =height[l]; sum+=lmax-height[l]; l++; } else{ if(rmax<height[r]) rmax = height[r]; sum+=rmax-height[r]; r--; } } return sum; } }