LCA-最近公共祖先的四种解法

洛谷模板题 P3379

给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

ST表

基本思路

树的构造-举个栗子

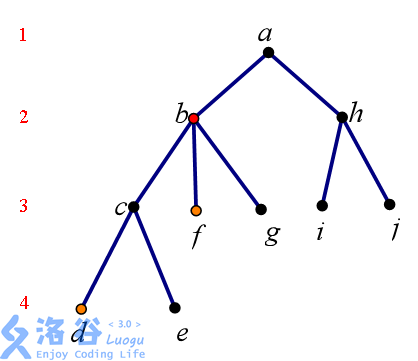
欧拉序

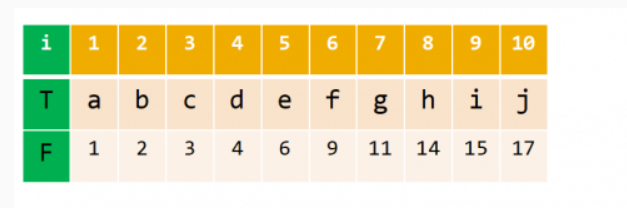
存储第一次出现的位置

使用链式前向星存储树的结构，首先求一棵树的欧拉序，然后根据两点的公共祖先就是欧拉序中（第一次出现时）两点位置区间内的深度最小点，
这一定理转化成RMQ最小问题，使用ST表时注意log2的复杂度比较高，ST表总体速度较慢，约900ms

#include<bits/stdc++.h>
#define FOR(i,a,b) for(int i=a;i<b;i++)
#define FOR2(i,a,b) for(int i=a;i<=b;i++)
#define sync ios::sync_with_stdio(false);
#define ll long long
#define INF  0x7f7f7f7f;
#define MAXN 1001000
#define ok1 cout<<"OK1"<<endl
#define ok2 cout<<"OK2"<<endl
#define ok3 cout<<"OK3"<<endl
#define MOD 10007
using namespace std;
int arr[MAXN][(int)log2(MAXN)+1],loc[MAXN][(int)log2(MAXN)+1],vis[MAXN/2],n,m,s,eu,cnt,ed=0,head[MAXN];
typedef struct{
	int from,to,next;
}EDGE;EDGE edges[MAXN];
inline int read()
{
    char ch=getchar();
    int x=0,f=1;
    while((ch>'9'||ch<'0')&&ch!='-')
        ch=getchar();
    if(ch=='-')
    {
        f=-1;
        ch=getchar();
    }
    while('0'<=ch&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}
inline void put(int x)
{
    if(x==0)
    {
        putchar('0');
        putchar('
');
        return;
    }
    int num=0;
    char c[25];
    while(x)
    {
        c[++num]=(x%10)+48;
        x/=10;
    }
    while(num)
        putchar(c[num--]);
    putchar('
');
    return ;
}
inline int log2(int x)
{
	int k=0;while(x>1)x=x>>1,k++;return k;
}
inline void dfs(int pre,int cur,int level)
{
	arr[++cnt][0]=level;//深度欧拉序 
	loc[++eu][0]=cur;//节点欧拉序 
	if(vis[cur]==0)vis[cur]=eu;//位置 
	for(int i=head[cur];i;i=edges[i].next)
	{
		if(edges[i].to==pre)continue;
		dfs(cur,edges[i].to,level+1);
		arr[++cnt][0]=level;
	}
	if(pre!=cur)
	{
		loc[++eu][0]=pre;
	}
}
inline void add(int a,int b)
{
	edges[++ed].from=a;
	edges[ed].to=b;
	edges[ed].next=head[a];
	head[a]=ed;
	return;
} 
int main()
{
//	freopen("t1.in","r",stdin);
//	freopen("t111.out","w",stdout);
	scanf("%d%d%d",&n,&m,&s);
	int a,b;
	eu=cnt=0;
	FOR(i,0,n-1)
	{
		scanf("%d%d",&a,&b);
		add(a,b);add(b,a);
	}
	dfs(0,s,1);
	
	//rmq
	int logh=log2(cnt);
	for(int h=1;h<=logh;h++)
	{
		for(int i=1;i+(1<<h)-1<=cnt;i++)
		{
			if(arr[i][h-1]<arr[i+(1<<h-1)][h-1])
			{//欧拉序对应的位置 
				arr[i][h]=arr[i][h-1];
				loc[i][h]=loc[i][h-1];
			}
			else{
				arr[i][h]=arr[i+(1<<h-1)][h-1];
				loc[i][h]=loc[i+(1<<h-1)][h-1];
			}
		}
	}
	FOR(i,0,m){
		scanf("%d%d",&a,&b);
		a=vis[a];b=vis[b];
		if(a>b)swap(a,b);
		int logk=log2(b-a+1);
		if(arr[a][logk]<arr[b-(1<<logk)+1][logk]){
			printf("%d
",loc[a][logk]); 
		} 
		else printf("%d
",loc[b-(1<<logk)+1][logk]);
	}
	return 0;
}

倍增

基本思路

先dfs处理树，记录每个节点上跳(2^{1 o {maxjump}})次能到达的祖先节点，

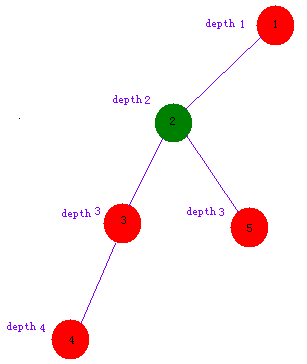
然后读取要求的点(a，b)，处理成同一深度后，若(b)是(a)的祖先，则返回b，
若不是，则同时上跳(2^{1 o{maxjump}})次，直到相等.

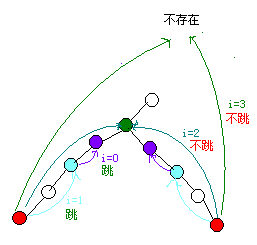
时间比ST表快，约550ms。预处理时间复杂度O(nlogn)，每次查询时间复杂度O(logn)

参考

https://blog.csdn.net/qq_42790311/article/details/81486742
https://blog.csdn.net/txl199106/article/details/53998831

#include<bits/stdc++.h>
#define FOR(i,a,b) for(int i=a;i<b;i++)
#define FOR2(i,a,b) for(int i=a;i<=b;i++)
#define ll long long
#define INF  0x7f7f7f7f;
#define MAXN 1000100
#define MOD 10007
using namespace std;
typedef struct{
	int from,to,next;
}EDGE;EDGE edges[MAXN];
int maxjump=(int)log2(MAXN)+1,head[MAXN],ed=0,n,m,s,a,b,dep[MAXN],jump[MAXN][(int)log2(MAXN)+1];
inline int read()
{
    char ch=getchar();
    int x=0,f=1;
    while((ch>'9'||ch<'0')&&ch!='-')
        ch=getchar();
    if(ch=='-')
    {
        f=-1;
        ch=getchar();
    }
    while('0'<=ch&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}
inline void put(int x)
{
    if(x==0)
    {
        putchar('0');
        putchar('
');
        return;
    }
    int num=0;
    char c[25];
    while(x)
    {
        c[++num]=(x%10)+48;
        x/=10;
    }
    while(num)
        putchar(c[num--]);
    putchar('
');
    return ;
}
inline int log2(int x)
{
	int k=0;while(x>1)x=x>>1,k++;return k;
}
inline void add(int a,int b)
{
	edges[++ed].from=a;
	edges[ed].to=b;
	edges[ed].next=head[a];
	head[a]=ed;
	return;
} 
void dfs(int cur,int pre)
{
	jump[cur][0]=pre;
	dep[cur]=dep[pre]+1;
	for(int i=1;i<maxjump;i++)
	{
		jump[cur][i]=jump[jump[cur][i-1]][i-1];//预处理 
	}
	for(int i=head[cur];i;i=edges[i].next)
	{
		if(edges[i].to!=pre)
			dfs(edges[i].to,cur);	
	} 
}
int lca(int x,int y)
{
	if(dep[x]<dep[y])
		swap(x,y);
//	for(int i=maxjump-1;i>=0;i--)
//		if((1<<i)<=dep[x]-dep[y])
//			x=jump[x][i];//处理成同一深度 
	while(dep[x]>dep[y])x=jump[x][] 
	if(x==y)//y是x的祖先 
		return x;
	for(int i=maxjump-1;i>=0;i--)
	{//一起倍增 
		if(jump[x][i]!=jump[y][i])
		{
			x=jump[x][i],y=jump[y][i];
		}
	 } 
	 return jump[x][0];//返回父节点 
}
int main()
{
	scanf("%d%d%d",&n,&m,&s);
	FOR(i,0,n-1)
	{
		scanf("%d%d",&a,&b);
		add(a,b);add(b,a);
	}
	dfs(s,0);
	FOR(i,0,m)
	{
		scanf("%d%d",&a,&b);
		printf("%d
",lca(a,b));	
	} 
	return 0;
}

Tarjan算法

基本思路

1. 先选择一个节点u为根节点，从根节点开始搜索。（标记u已访问过）
2. 遍历该点u的所有儿子节点v，并标记v已访问过。
3. 若v还有儿子节点，对v重复ii操作，否则进入下一操作。
4. 把v合并到u上（并查集）。
5. 把当前的点设为u，遍历与u有询问关系的节点v。
6. 如果v在之前已经被访问过，那么u和v的最近公共祖先就是v通过并查集合并后的父亲节点（注意是合并后），即当前的find（v）。
   预处理时间复杂度O(nlogn),每次查询时间复杂度O(1)，总时间复杂度是O(nlogn+q),约400ms
   Tarjan伪代码

Tarjan(u)//marge和find为并查集合并函数和查找函数
{
    for each(u,v)    //访问所有u子节点v
    {
        Tarjan(v);        //继续往下遍历
        marge(u,v);    //合并v到u上
        标记v被访问过;
    }
    for each(u,e)    //访问所有和u有询问关系的e
    {
        如果e被访问过;
        u,e的最近公共祖先为find(e);
    }
}

参考

https://www.cnblogs.com/JVxie/p/4854719.html

#include<bits/stdc++.h>
#define FOR(i,a,b) for(int i=a;i<b;i++)
#define FOR2(i,a,b) for(int i=a;i<=b;i++)
#define ll long long
#define INF  0x7f7f7f7f;
#define MAXN 1000100
#define MOD 10007
using namespace std;
typedef struct{
	int from,to,next;
}EDGE;EDGE edges[MAXN],vedges[MAXN];
int head[MAXN],vhead[MAXN],ed=0,ved=0,n,m,s,a,b,fa[MAXN],vis[MAXN],lca[2*MAXN];
inline int read()
{
    char ch=getchar();
    int x=0,f=1;
    while((ch>'9'||ch<'0')&&ch!='-')
        ch=getchar();
    if(ch=='-')
    {
        f=-1;
        ch=getchar();
    }
    while('0'<=ch&&ch<='9')
    {
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x*f;
}
inline void put(int x)
{
    if(x==0)
    {
        putchar('0');
        putchar('
');
        return;
    }
    int num=0;
    char c[25];
    while(x)
    {
        c[++num]=(x%10)+48;
        x/=10;
    }
    while(num)
        putchar(c[num--]);
    putchar('
');
    return ;
}
inline int log2(int x)
{
	int k=0;while(x>1)x=x>>1,k++;return k;
}
inline void add(int a,int b)
{
	edges[++ed].from=a;
	edges[ed].to=b;
	edges[ed].next=head[a];
	head[a]=ed;
	return;
} 

inline void vadd(int a,int b)
{
	vedges[++ved].from=a;
	vedges[ved].to=b;
	vedges[ved].next=vhead[a];
	vhead[a]=ved;
	return ;
}
inline int find(int x)
{
	if(x!=fa[x]) fa[x]=find(fa[x]);
	return fa[x];
}
void tarjan(int u)
{
	vis[u]=true;
	for(int i=head[u];i;i=edges[i].next)
	{
		if(vis[edges[i].to])continue;//访问过则跳过 
		tarjan(edges[i].to);
		fa[edges[i].to]=u;//合并 
	}
	for(int i=vhead[u];i;i=vedges[i].next)
	{
		if(vis[vedges[i].to])
		{
			lca[i]=find(vedges[i].to);//寻找已经被访问过的点的祖先
			if(i&1)//询问了两遍
				lca[i+1]=lca[i];
			else
				lca[i-1]=lca[i]; 
		}
	}
}
int main()
{
	FOR(i,0,MAXN)fa[i]=i;
	scanf("%d%d%d",&n,&m,&s);
	FOR(i,0,n-1)
	{//读入边 
		scanf("%d%d",&a,&b);
		add(a,b);add(b,a);
	}
	FOR(i,0,m)
	{//离线查询 
		scanf("%d%d",&a,&b);
		vadd(a,b),vadd(b,a);
	}
	tarjan(s);
	for(int i=1;i<=m;i++)
		put(lca[i*2]);
	return 0;
}

树链剖分

约束RMQ

参考

https://www.cnblogs.com/ghostcai/p/9280720.html
https://blog.csdn.net/qq_36909245/article/details/80055114