【LGOJ4147】玉蟾宫

一片土地被分成N*M个格子，每个格子里写着R'或者"'F'
R代表这块土地被赐予了rainbow , F代表这块土地被赐予了freda
现在freda要找一块矩形土地,要求这片土地都标着'F'并且面积最大
输出最大的符合要求的土地的面积*3
（原题面中是指有三个人每个人给你S两银子，其实就是乘三……）

考场现学“悬线法”……
说实话，这种方法很难想到，但是十分巧妙

先讲一下另一种可以通过此题的不优算法：
我们把此题抽象为一个01矩阵，要求找到最大的全1子矩阵
由于答案具有某种意义上的单调性（如果有面积为S的矩阵符合，那么其约数大小的矩阵也符合）
那么我们二分面积，每次check是否存在这么大的矩阵

首先使用二维前缀和，统计出任意矩阵中1的个数，以及预处理约数
然后对于每个我们需要check的mid，(n^2)枚举它的位置
如果它所在的位置正好有面积那么多1，就说明存在

前缀和和check是(Theta{(n^2)})的
预处理约数个数，以及二分面积都是(Theta{(log^{2} m)})的（m是最大的面积）
所以总复杂度是(Theta{(n^2log^2 m)})，显然会T
在随机数据下，我们把m设小一点即可过……

这里介绍一下玄学的悬线法——

如下图，它是一个01矩阵（灰色为0，白色为1）

[ ext{tqr又乱画了一个图} ]

我们在这张图上模拟实现一下这个算法：

这个算法的朴素思路是什么呢？选取一列连续的1，定为所要扩展的矩形的高

[ ext{如图，这个粉色块即将扩展} ]

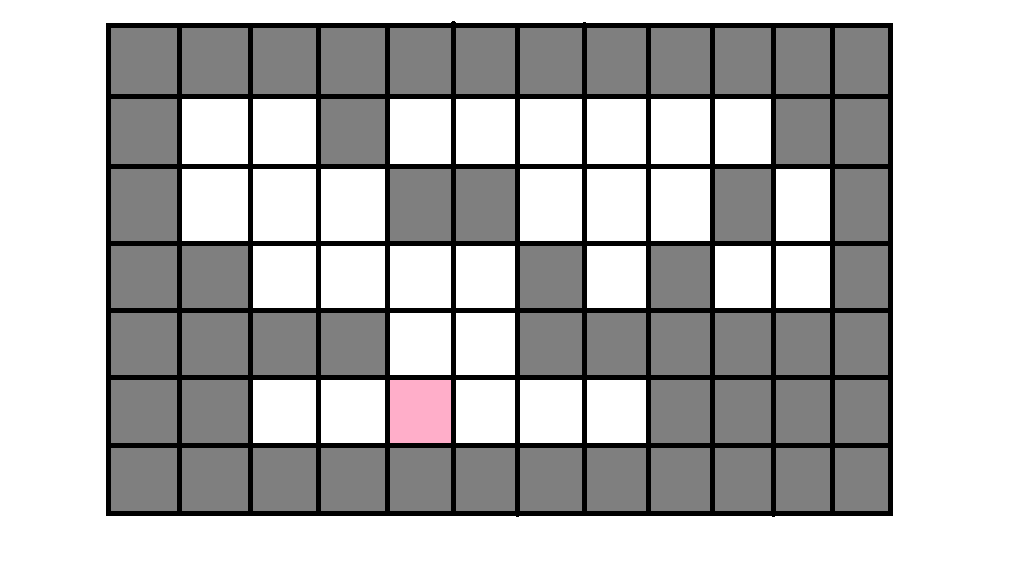
然后我们保持这个高度不变，让这个矩形向两边扩展！

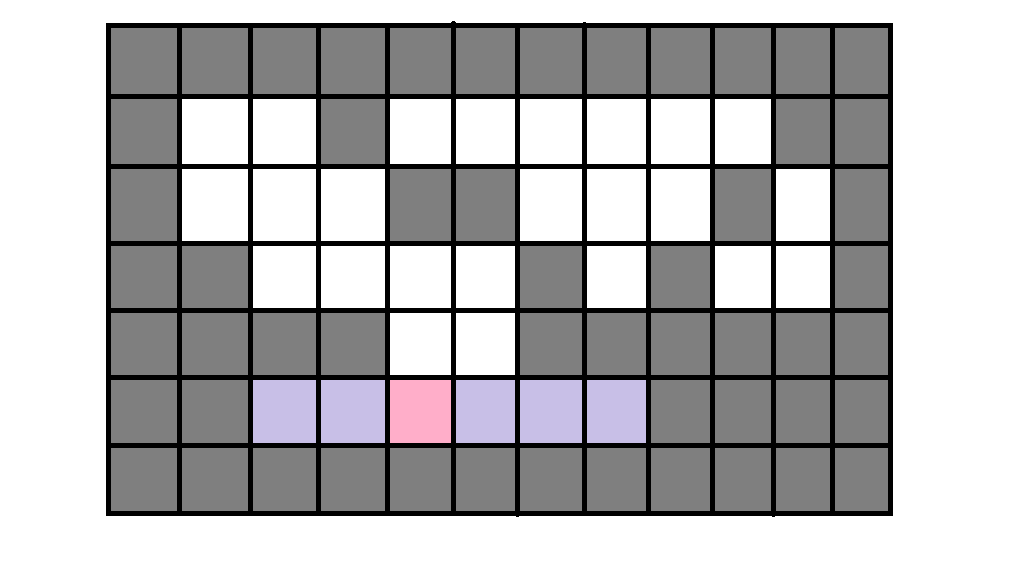
就这样，我们得到了一个面积为5的符合条件的矩形！

然后我们把它的高度增加一点点……

继续扩展

现在得到的是一个面积为4的矩形……

同理，继续进行操作，我们得到的就是面积为6的矩形

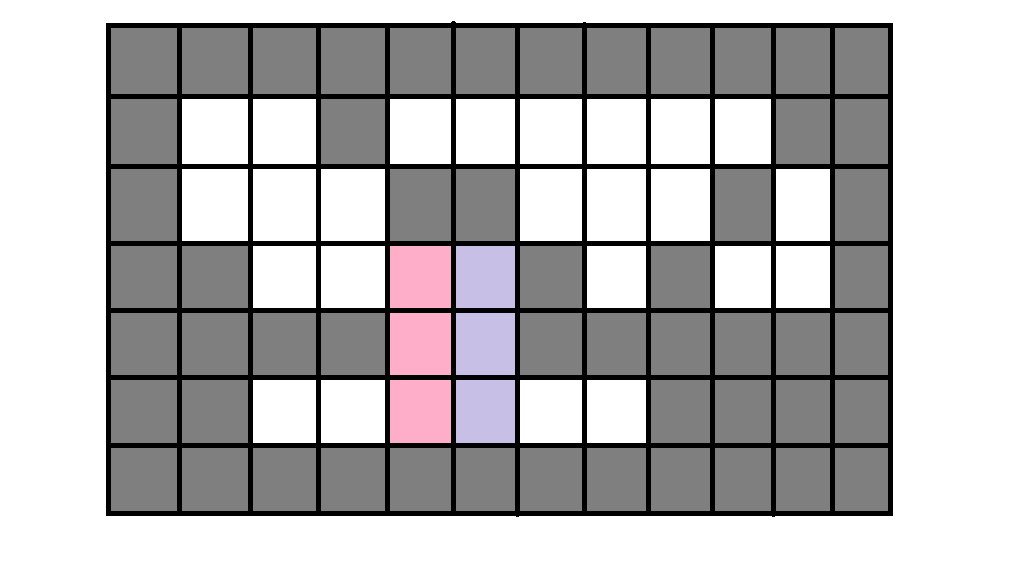
简单地看一下图，可知这个矩形已经是最优的了（虽然不是唯一最优的）

那么我们就得到了它的朴素思路：

1. 确定一个连续的高
2. 将其向左右扩展，更新答案

但是这样的时间复杂度是(Theta{(n^3)})的，我们考虑下怎么用dp的思路优化它……

首先，我们需要以下的值：

1. 一个点往上能扩展到哪里（u数组），定为高
2. 一个点往左能扩展到哪里（l数组）
3. 一个点往右能扩展到哪里（r数组）

很显然的，l和r不需要对于每个点(Theta{(n)})地求，它可以由同一行的左（右）一个格子转移过来

for(register int i=1;i<=n;++i)
	for(register int j=2;j<=m;++j)
		if(a[i][j-1]&&a[i][j]) l[i][j]=l[i][j-1];
for(register int i=1;i<=n;++i)
	for(register int j=m-1;j>=1;--j)
		if(a[i][j+1]&&a[i][j]) r[i][j]=r[i][j+1];

这样，我们就(Theta{(n^2)})地预处理出了每个点的l和r

等等，但这样转移的话，不会出问题吗？？？

这样的一个矩形，如果它的高被更新之后，l和r怎么更新？

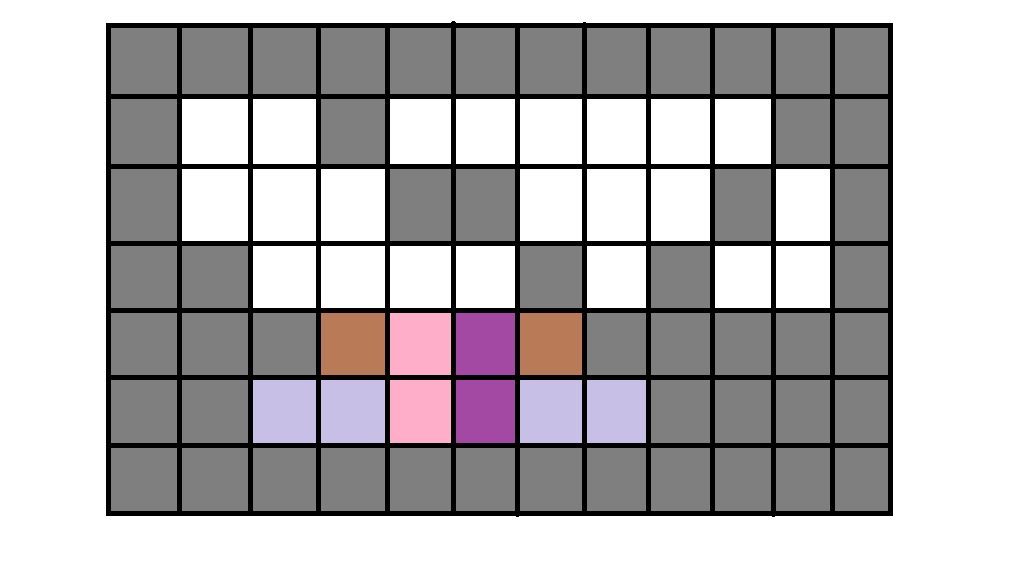
看到，棕色的部分阻挡了下面扩展的路径，而且大矩形的l和r正好是之前的l和r与这一行的l和r的最大值和最小值！（拒绝感性理解）

所以当u有转移的时候，l和r也会跟着转移（压缩范围）

其中l会往右靠（如果有障碍的话），r会往左靠（同理），于是l取max，r取min

for(register int i=1;i<=n;++i)
{
	for(register int j=1;j<=m;++j)
	{
		if(i-1&&a[i-1][j]&&a[i][j])
		{
			u[i][j]=u[i-1][j]+1;
			l[i][j]=max(l[i][j],l[i-1][j]);
			r[i][j]=min(r[i][j],r[i-1][j]);
		}
		ans=max(ans,(r[i][j]-l[i][j]+1)*u[i][j]);
	}
}

其实到这里，这个算法就结束了……
时间复杂度非常优秀，自己速速理解一下？

最后放上本题代码：

#include<bits/stdc++.h>
using namespace std;

int n,m,ans;
bool a[1005][1005];
char c[2];
int u[1005][1005],l[1005][1005],r[1005][1005];

template<class T>inline void read(T &res)
{
	char c;T flag=1;
	while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;res=c-'0';
	while((c=getchar())>='0'&&c<='9')res=res*10+c-'0';res*=flag;
}

int main()
{
	read(n);read(m);
	for(register int i=1;i<=n;++i)
	{
		for(register int j=1;j<=m;++j)
		{
            scanf("%s",c);
			if(c[0]=='F') a[i][j]=1;
			else a[i][j]=0;
			if(a[i][j]) u[i][j]=1,l[i][j]=r[i][j]=j;
		}
	}
	for(register int i=1;i<=n;++i)
		for(register int j=2;j<=m;++j)
			if(a[i][j-1]&&a[i][j]) l[i][j]=l[i][j-1];
	for(register int i=1;i<=n;++i)
		for(register int j=m-1;j>=1;--j)
			if(a[i][j+1]&&a[i][j]) r[i][j]=r[i][j+1];
	for(register int i=1;i<=n;++i)
	{
		for(register int j=1;j<=m;++j)
		{
			if(i-1&&a[i-1][j]&&a[i][j])
			{
				u[i][j]=u[i-1][j]+1;
				l[i][j]=max(l[i][j],l[i-1][j]);
				r[i][j]=min(r[i][j],r[i-1][j]);
			}
			ans=max(ans,(r[i][j]-l[i][j]+1)*u[i][j]);
		}
	}
	printf("%d
",ans*3);
	return 0;
}