Fleury（弗罗莱）算法求欧拉回路

转自http://www.cnblogs.com/Lyush/archive/2013/04/22/3036659.html

上面是摘自图论书上的定义。

算法在运行过程中删除了所有已走的路径，也就是说途中残留了所有没有行走的边。根据割边的定义，如果在搜索过程中遇到割边意味着当前的搜索路径需要改进，即提前输出某一个联通子集的访问序列，这样就能够保证访问完其中联通子图中后再通过割边访问后一个联通子图，最后再沿原路输出一开始到达该点的路径。如果只有割边可以扩展的话，只需要考虑先输出割边的另一部分联通子集访问序列。

样例图：

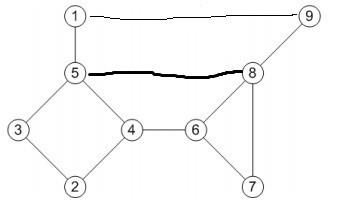
代码如下：

#include <cstdlib>
#include <cstring>
#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
/*
弗罗莱算法
*/

int stk[1005];
int top;
int N, M, ss, tt;
int mp[1005][1005];

void dfs(int x) {
    stk[top++] = x;
    for (int i = 1; i <= N; ++i) {
        if (mp[x][i]) {
            mp[x][i] = mp[i][x] = 0; // 删除此边
            dfs(i);
            break;
        }    
    }
}
/*
9 12
1 5
1 9
5 3
5 4
5 8
2 3
2 4
4 6
6 7
6 8
7 8
8 9

path:
5 8 7 6 8 9 1 5 3 2 4 6
*/

void fleury(int ss) {
    int brige;
    top = 0;
    stk[top++] = ss; // 将起点放入Euler路径中
    while (top > 0) {
        brige = 1;
        for (int i = 1; i <= N; ++i) { // 试图搜索一条边不是割边（桥） 
            if (mp[stk[top-1]][i]) {
                brige = 0;
                break;
            }
        }
        if (brige) { // 如果没有点可以扩展，输出并出栈
            printf("%d ", stk[--top]);
        } else { // 否则继续搜索欧拉路径
            dfs(stk[--top]);
        }
    }
}

int main() {
    int x, y, deg, num;
    while (scanf("%d %d", &N, &M) != EOF) {
        memset(mp, 0, sizeof (mp));
        for (int i = 0; i < M; ++i) {
            scanf("%d %d", &x, &y);
            mp[x][y] = mp[y][x] = 1;
        }
        for (int i = 1; i <= N; ++i) {
            deg = num = 0;
            for (int j = 1; j <= N; ++j) {
                deg += mp[i][j];    
            }
            if (deg % 2 == 1) {
                ss = i, ++num;
                printf("%d
", i);
            }
        }
        if (num == 0 || num == 2) {
            fleury(ss);
        } else {
            puts("No Euler path");
        }
    }
    return 0;    
}

　　

stack<int>S;
int edge[MAXN][MAXN];
int n,m;

void dfs(int x){
    S.push(x);
    for(int i=1;i<=n;i++){
        if(edge[x][i]>0){
            edge[i][x]=edge[x][i]=0;//删除此边
            dfs(i);
            break;
        }
    }
}

//Fleury算法的实现
void Fleury(int x){
    S.push(x);
    while(!S.empty()){
        int b=0;
        for(int i=1;i<=n;i++){
            if(edge[S.top()][i]>0){
                b=1;
                break;
            }
        }
        if(b==0){
            printf("%d",S.top());
            S.pop();
        }else {
            int y=S.top();
            S.pop();
            dfs(y);//如果有，就dfs
        }
    }
    printf("
");
}