数字系统(数码系统)定义了如何用独特的符号来表示一个数字。
数字系统分为位置化数字系统和非位置化数字系统。
位置化数字系统
在位置化数字系统中,数字中符号所占据的位置决定了其表示的值。
位置化数字系统的表示
±(Sk-1Sk-2…S3S2S1S0.S-1S-2S-3…S-L)b;
位置化数字系统的(十进制)值
N=±Sk-1×bk-1+Sk-2×bk-2+…+S3×b3+S2×b2+S1×b1+S0×b0+S-1×b-1+S-2×b-2+S-3×b-3+…+S-L×b-L;
其中:
- S是一套符号集。
- b是基数。
- 从小数点开始,b的幕可以从一个方向由0到k-l,还可以从另一个方向由-1到-L;
- 即b的非负数次幕与该数字的整数部分有关,而b的负数次幂与该数字的小数部分有关;
- ±符号表示该数字可正可负。
十进制系统(Decimal)
- 基数b=10;
- 符号集S={0,1,2,3,4,5,6,7,8,9};
- 整数值表示: N = ±Sk-1×10k-1+Sk-2×10k-2+…+S3×103+S2×102+S1×101+S0×100;
- 实数值表示: N = ±Sk-1×10k-1+Sk-2×10k-2+…+S3×103+S2×102+S1×101+S0×100+S-1×10-1+S-2×10-2+S-3×10-3+…+S-L×10-L;
二进制系统(Binary)
- 基数b=2;
- 符号集S={0,1};
- 整数值表示: N = ±Sk-1×2k-1+Sk-2×2k-2+…+S3×23+S2×22+S1×21+S0×20;
- 实数值表示: N = ±Sk-1×2k-1+Sk-2×2k-2+…+S3×23+S2×22+S1×21+S0×20+S-1×2-1+S-2×2-2+S-3×2-3+…+S-L×2-L;
二进制的部分权值
| 权 | (值)2 | (值)10 |
| 20 | 1 | 1 |
| 21 | 10 | 2 |
| 22 | 100 | 4 |
| 23 | 1000 | 8 |
| 24 | 10000 | 16 |
| 25 | 100000 | 32 |
| 26 | 1000000 | 64 |
| 27 | 10000000 | 128 |
| 28 | 100000000 | 256 |
| 29 | 1000000000 | 512 |
| 210 | 10000000000 | 1024 |
十六进制系统(Hexadecimal)
- 基数b=16;
- 符号集S={0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F};
- A,B,C,D,E,F分别等于10,11,12,13,14,15;
- 整数值表示: N = ±Sk-1×16k-1+Sk-2×16k-2+…+S3×163+S2×162+S1×161+S0×160;
- 实数值表示:尽管一个实数可以用十六进制系统表示,但并不常见。
八进制系统(Octal)
- 基数b=8;
- 符号集S={0,1,2,3,4,5,6,7};
- 整数值表示: N = ±Sk-1×8k-1+Sk-2×8k-2+…+S3×83+S2×82+S1×81+S0×80;
- 实数值表示:尽管一个实数可以用八进制系统表示,但并不常见。
四种进位计数制小结
| 进位计数制 | 形式表示 | 基数 | 符号集 | Example | Or Example |
| 十进制 | D | 10 | 0,1,2,3,4,5,6,7,8,9 | (123.12) 10 | (123.12)D |
| 二级制 | B | 2 | 0,1 | (1001.11)2 | (1001.11)B |
| 八进制 | O | 8 | 0,1,2,3,4,5,6,7 | (156.23) 8 | (156.23)O |
| 十六进制 | H | 16 | 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F | (A2C.A1)16 | (A2C.A1)H |
比较四种进位计数制表示同一数字
| 十进制 | 二进制 | 八进制 | 十六进制 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
数字 15 在十进制中使用2个数码,在二进制中使用4个数码,在八进制中使用2个数码,在十六进制中仅仅使用1个数码;十六进制表示法显然是最短的。即在采用不同的数制表示同一个数时,基数越大,则使用的位数越小。所以在程序的书写中,一般采用八进制或十六进制表示数据。
进制转换——R进制转换为十进制
将R进制数按权展开求和即可等到相应的十进制数。
Example:将这三个数转换为十进制数值。
(10110)B = (1×24+0×23+1×22+1×21+0×20)D
= (16+0+4+2+0)D
= (22)D
(234)O = (2×82+3×81+4×80)D
= (128+24+4)D
= (156)D
(234)H = (2×162+3×161+4×160)D
= (512+48+4)D
= (564)D
进制转换——R进制转换为十进制
整数部分:
将十进制整数转换为R进制数,采用“除R取余法”,即将十进制整数连续地除以R取余数,直到商为0。将最后一个余数最为R进制数的第一位,将倒是第二个余数作为R进制数的第二位,依次类推得到R进制数的整数部分。
小数部分:
小数部分的转换采用“乘R取整法”,即将十进制小数部分不断乘以R取整,直到小数部分为0或达到要求的精度(当小数部分永远不会达到0时)。取得的整数的排列次序与取得顺序一致,即首次取得的整数作为R进制数小数部分的第一位,最后一次取得的整数作为R进制数小数部分的最后一位。
Example1:
(225.8125)D → 二进制数
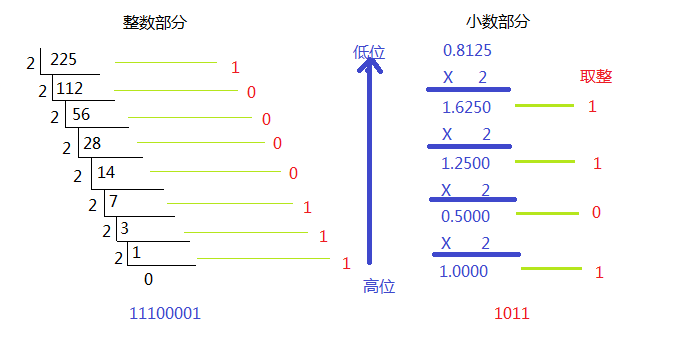
所以 (225.8125)D = (11100001.1101)B
Example2:
将十进制数225.15转换八进制数。
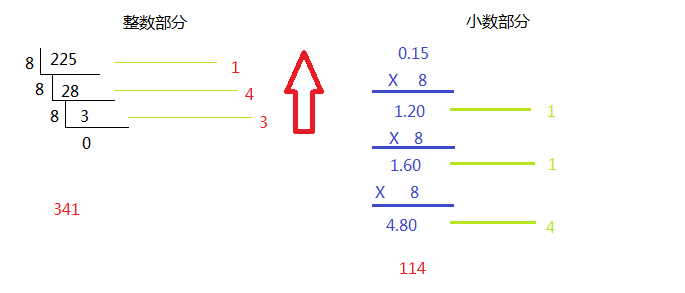
所以(225.15)D = (341.114)O。
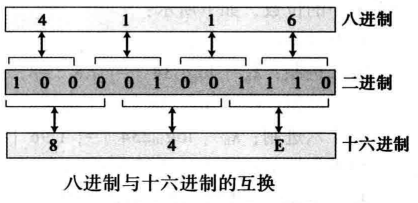
进制转换——八进制十六进制之间的转换
计算及内部数据的表示和运算非常适合二进制,但位数过长 。所以在书写程序和数据时,经常采用八进制或十六进制,这两种进位计数制相比于二进制位数要简短得多。
八进制与十六进制之间的转换依赖于二进制、八进制、十六进制之间的特殊关系。
81 = 23; 1位八进制数相当于3位二进制数。
161 = 24; 1位十六进制数相当于4位二进制数。
二进制数、八进制数、十六进制数之间的关系表
| 八进制数 | 对应二进制数 | 十六进制数 | 对应二进制数 | 十六进制数 | 对应二进制数 |
| 0 | 000 | 0 | 0000 | 8 | 1000 |
| 1 | 001 | 1 | 0001 | 9 | 1001 |
| 2 | 010 | 2 | 0010 | A | 1010 |
| 3 | 011 | 3 | 0011 | B | 1011 |
| 4 | 100 | 4 | 0100 | C | 1100 |
| 5 | 101 | 5 | 0101 | D | 1101 |
| 6 | 110 | 6 | 0110 | E | 1110 |
| 7 | 111 | 7 | 0111 | F | 1111 |
根据这种对应关系。
将二进制转换为八进制时,从小数点开始分别向左右两边分组,每3位为一组,两头不足3位补0。再分别进行转换。
将二进制转换为十六进制时,从小数点开始分别向左右两边分组,每4位为一组,两头不足4位补0。再分别进行转换。
Example1:将二进制数(10101011.110101)B分别转换为八进制数和十六进制数。
(10101011.110101)B = (010 101 011 • 110 101)B = (253.65)O {010=2,101=5,011=3,110=6,101=5};
(10101011.110101)B = (1010 1011 • 1101 0100)B = (AB.D4)H {1010=A,1011=B,1101D,0100=4};
同样的,将八进制数或十六进制数转换为二进制数,将八进制数的1位转换为二进制数的3位,将十六进制数的1位转换为二进制数的4位即可。
八进制数与十六进制数之间的转换将二进制数作为中间量来完成。
非位置化数字系统(了解即可)
如罗马数字
1-Ⅰ、2-Ⅱ、3-Ⅲ、4-Ⅳ、5-Ⅴ、6-Ⅵ、7-Ⅶ、8-Ⅷ、9-Ⅸ。
10-Ⅹ、11-Ⅺ、12-Ⅻ、13-XIII、14-XIV、15-XV、16-XVI、17-XVII、18-XVIII、19-XIX、20-XX