福哥答案2021-01-23:
这道题复杂度太高,短时间内很难写出来。面试的时候不建议手撕代码。
一个存节点的map+一个存桶的map+一个存桶的双向链表。桶本身也是一个双向链表。
存节点的map:key是键,value是节点。
存桶的map:key是次数,value是桶。
代码用golang编写,代码如下:
package main
import (
"container/list"
"fmt"
)
func main() {
cache := Constructor(2)
cache.Put(1, 1)
cache.Put(2, 2)
cache.Get(1) // 返回 1
cache.Put(3, 3) // 去除键 2
cache.Get(2) // 返回 -1(未找到)
cache.Get(3) // 返回 3
cache.Put(4, 4) // 去除键 1
cache.Get(1) // 返回 -1(未找到)
cache.Get(3) // 返回 3
cache.Get(4) // 返回 4
}
type LFUCache struct {
Cap int
Len int
//map缓存,键存key,值存kv和前后
KeyCache map[int]*list.Element //key存键,value存节点
List *list.List
FreqCache map[int]*list.Element //key存次数,value存桶
}
func Constructor(capacity int) LFUCache {
ret := LFUCache{}
ret.Cap = capacity
ret.KeyCache = make(map[int]*list.Element) //元素存节点
ret.FreqCache = make(map[int]*list.Element) //元素存桶
ret.List = list.New()
return ret
}
func (this *LFUCache) Get(key int) int {
//已经找到当前元素了
v := this.KeyCache[key]
if v == nil {
fmt.Println(-1)
return -1
}
//移动
this.curNodeMoveToNextBucket(v)
//返回当前元素的值
fmt.Println(v.Value.([]int)[1])
return v.Value.([]int)[1]
}
//当前节点移动到下一个桶
func (this *LFUCache) curNodeMoveToNextBucket(v *list.Element) {
//根据当前节点的次数找到当前桶
curbucket := this.FreqCache[v.Value.([]int)[2]]
//找下一桶,找不到创建新桶
nextbucket := this.FreqCache[v.Value.([]int)[2]+1]
if nextbucket == nil {
nextbucket = this.List.InsertAfter(list.New(), curbucket)
this.FreqCache[v.Value.([]int)[2]+1] = nextbucket
}
//把当前节点放在下一桶里
//nextbucket.Value.(*list.List).PushBack(v.Value),这样的代码,leetcode不能通过。原因是元素移动后,已经不是以前的元素了。所以map需要重新赋值。这个错误,我花了1个小时才找到,请谨慎。
this.KeyCache[v.Value.([]int)[0]] = nextbucket.Value.(*list.List).PushBack(v.Value)
//当前桶删除当前节点
curbucket.Value.(*list.List).Remove(v)
//如果当前桶为空,直接删除当前桶。
if curbucket.Value.(*list.List).Len() == 0 {
this.List.Remove(curbucket)
delete(this.FreqCache, v.Value.([]int)[2])
}
//当前节点次数加1
v.Value.([]int)[2]++
}
func (this *LFUCache) Put(key int, value int) {
if this.Cap == 0 {
return
}
if v, ok := this.KeyCache[key]; ok { //缓存里有
//修改值
v.Value.([]int)[1] = value
//移动
this.curNodeMoveToNextBucket(v)
} else { //缓存里没有
if this.Len == this.Cap {
//获取可能需要删除的桶
deleteBucket := this.List.Front()
//获取需要删除的元素
deleteE := deleteBucket.Value.(*list.List).Front()
//删除元素
delete(this.KeyCache, deleteE.Value.([]int)[0])
deleteBucket.Value.(*list.List).Remove(deleteE)
//可能需要删除的桶如果没有元素,删除桶。并且需要删除的元素的次数不是1
if deleteBucket.Value.(*list.List).Len() == 0 {
this.List.Remove(deleteBucket)
delete(this.FreqCache, deleteE.Value.([]int)[2])
}
} else {
this.Len++
}
//获取次数为1的桶
oneTimeBucket := this.FreqCache[1]
//获取不到就创建桶
if oneTimeBucket == nil {
oneTimeBucket = this.List.PushFront(list.New())
this.FreqCache[1] = oneTimeBucket
}
this.KeyCache[key] = oneTimeBucket.Value.(*list.List).PushBack([]int{key, value, 1})
}
}
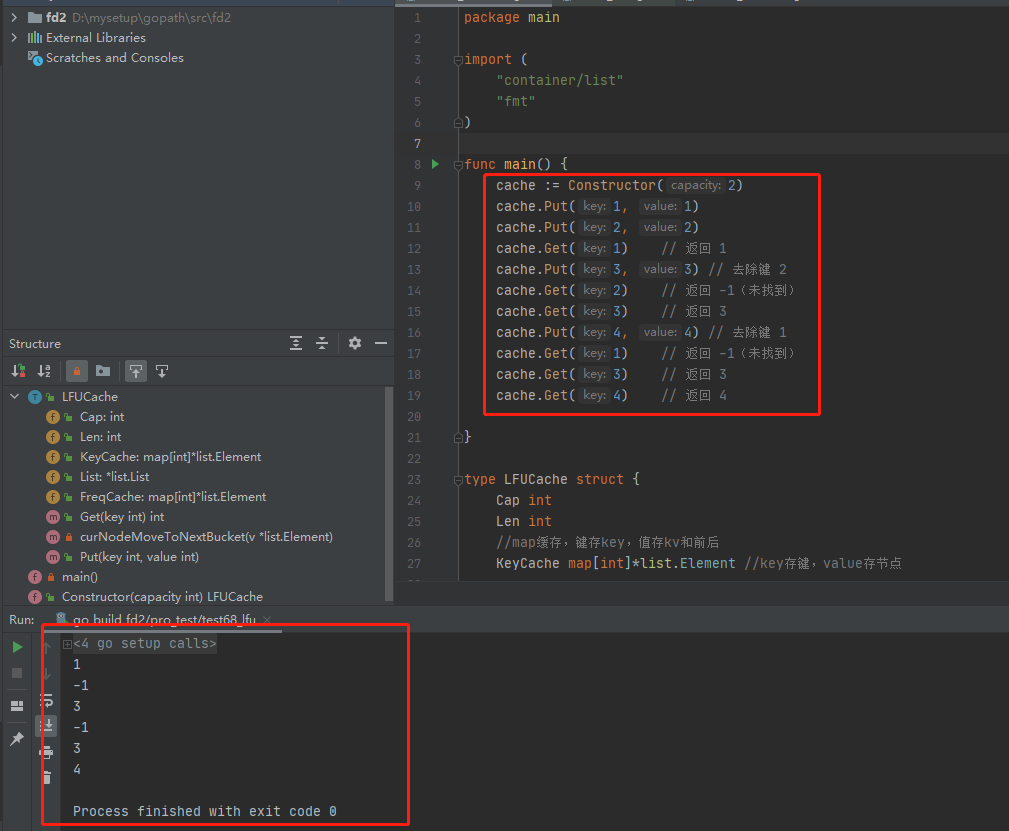
执行结果如下: