Graph Attention Networks
2018-02-06 16:52:49
Abstract：
本文提出一种新颖的 graph attention networks (GATs), 可以处理 graph 结构的数据，利用 masked self-attentional layers 来解决基于 graph convolutions 以及他们的预测 的前人方法（prior methods）的不足。
对象：graph-structured data.
方法：masked self-attentional layers.
目标：to address the shortcomings of prior methods based on graph convolutions or their approximations.
具体方法：By stacking layers in which nodes are able to attend over their neghborhood's feature. We enables specifying different weights to different nodes in a neighborhood, without requiring any kinds of costly matrix operation or depending on knowing the graph structure upfront.
Introduction：
Background：CNN 已经被广泛的应用于各种 grid 结构的数据当中，各种 task 都取得了不错的效果，如：物体检测，语义分割，机器翻译等等。但是，有些数据结构，不是这种 grid-like structure 的，如：3D meshes, social networks, telecommunication networks, biological networks, brain connection。
已经有多个尝试将 RNN 和 graph 结构的东西结合起来，来进行表示。
目前，将 convolution 应用到 the graph domain，常见的有两种做法：
1. spectral approaches
2. non-spectral approaches (spatial based methods)
文章对这两种方法进行了简要的介绍，回顾了一些最近的相关工作。
然后就提到了 Attention Mechanisms，这种思路已经被广泛的应用于各种场景中。其中一个优势就是：they allow for dealing with variable sized inputs, focusing on the most relvant parts of the input to make decisions。当 attention 被用来计算 single sequence 的表示时，通常被称为：self-attention or intra-attention。将这种方法和 CNN/RNN 结合在一起，就可以得到非常好的结果了。
受到最新工作的启发，我们提出了 attention-based architecture 来执行 node classification of graph-structured data。This idea is to compute the hidden representations of each node in the graph, by attending over its neighbors, following a self-attention stategy。这个注意力机制有如下几个有趣的性质：
1. 操作是非常有效的。
2. 可应用到有不同度的 graph nodes，通过给其紧邻指定不同的权重；
3. 这个模型可以直接应用到 inductive learning problems, including tasks where the model has to generalize to completely unseen graphs.
Our approach of sharing a neural network computation across edges is reminiscent of the formulation of relational networks (Santoro et al., 2017), wherein relations between objects (regional features from an image extracted by a convolutional neural network) are aggregated across all object pairs, by employing a shared mechanism.
作者在三个数据集上进行了实验，达到顶尖的效果，表明了 attention-based models 在处理任意结构的 graph 的潜力。
GAT Architecture ：
1. Graph Attentional Layer
本文所提出 attentional layer 的输入是 一组节点特征（a set of node features），
其中，N 是节点的个数，F 是每个节点的特征数。该层产生一组新的节点特征，作为其输出，即：
。
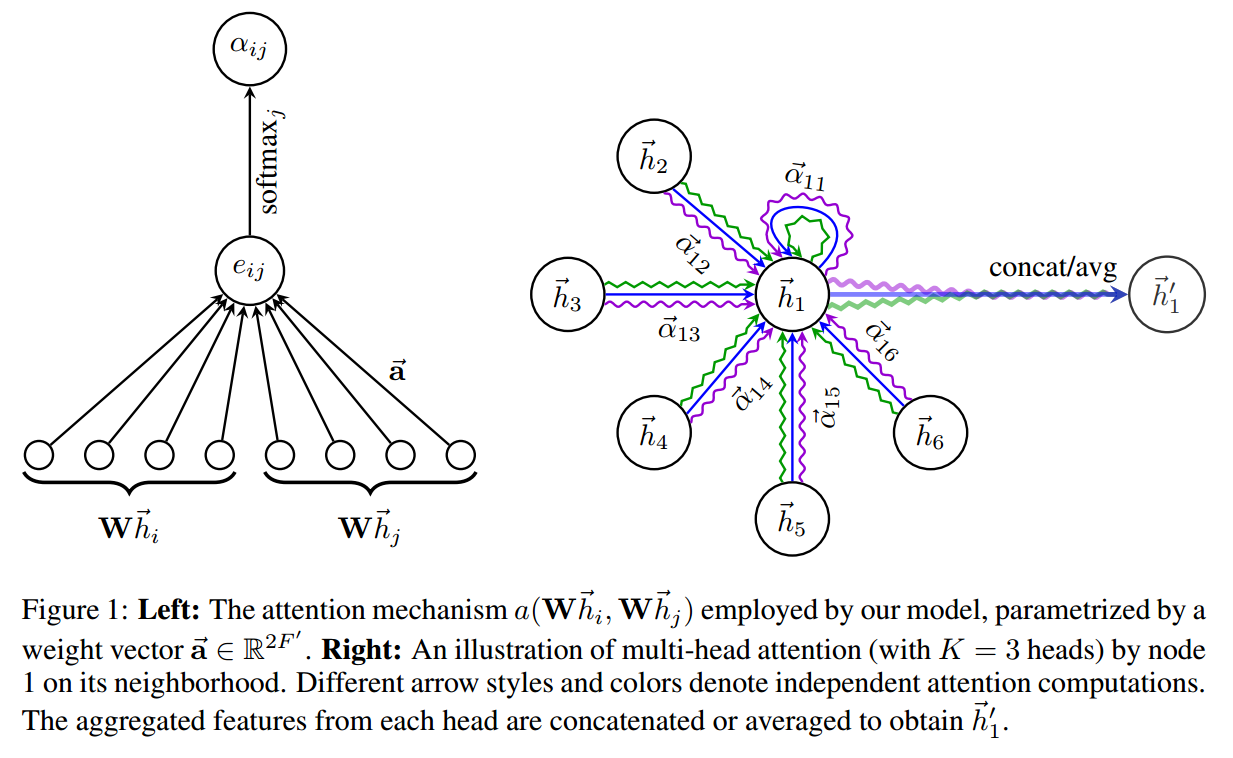
为了得到充分表达能力，将输入特征转换为高层特征，至少我们需要一个可学习的线性转换（one learnable linear transformation）。为了达到该目标，作为初始步骤，一个共享的线性转换，参数化为 weight matrix，W，应用到每一个节点上。我们然后在每一个节点上，进行 self-attention --- a shared attentional mechanism a：计算 attention coefficients
表明 node j's feature 对 node i 的重要性。最 general 的形式，该模型允许 every node to attend on every other node, dropping all structural information. 我们将这种 graph structure 通过执行 masked attention 来注射到该机制当中 --- 我们仅仅对 nodes $j$ 计算 $e_{ij}$，其中，graph 中节点 i 的一些近邻，记为：$N_{i}$。在我们的实验当中，这就是 the first-order neighbors of $i$。
为了使得系数简单的适应不同的节点，我们用 softmax function 对所有的 j 进行归一化：
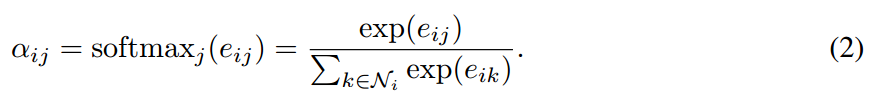
在我们的实验当中，该 attention 机制 a 是一个 single-layer feedforward neural network，参数化为 权重向量 
。全部展开，用 attention 机制算出来的系数，可以表达为：
其中，$*^T$ 代表 转置，|| 代表 concatenation operation。
一旦得到了，该归一化的 attention 系数可以用来计算对应特征的线性加权，可以得到最终的每个节点的输出向量：
为了稳定 self-attention 的学习过程，我们发现将我们的机制拓展到 multi-head attention 是有好处的，类似于：Attention is all you need. 特别的，K 个独立的 attention 机制执行公式（4）的转换，然后将其特征进行组合，得到下面的特征输出：
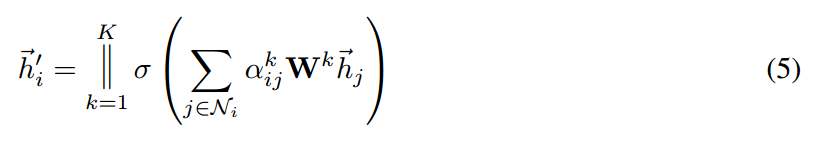
特别的，如果我们执行在 network 的最后输出层执行该 multi-head attention，concatenation 就不再是必须的了，相反的，我们采用 averaging，推迟执行最终非线性，
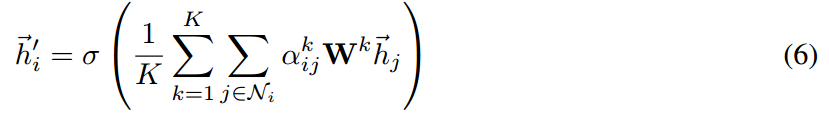
所提出 attention 加权机制的示意图，如下所示：
