1、线性可分VS线性不可分
对于一个分类问题,通常可以分为线性可分与线性不可分两种 。如果一个分类问题可以使用线性判别函数正确的分类,则称该问题为线性可分。如图所示为线性可分,否则为线性不可分:
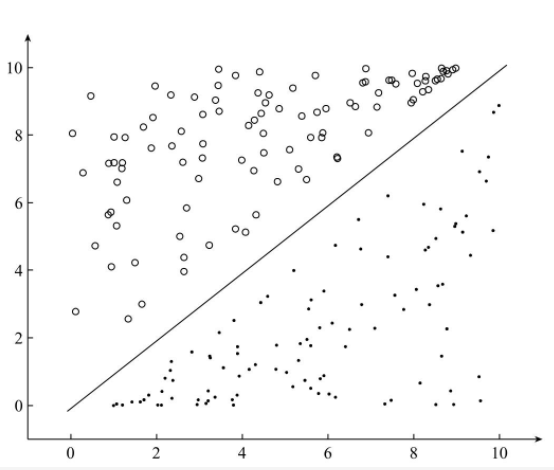
下图为线性不可分:
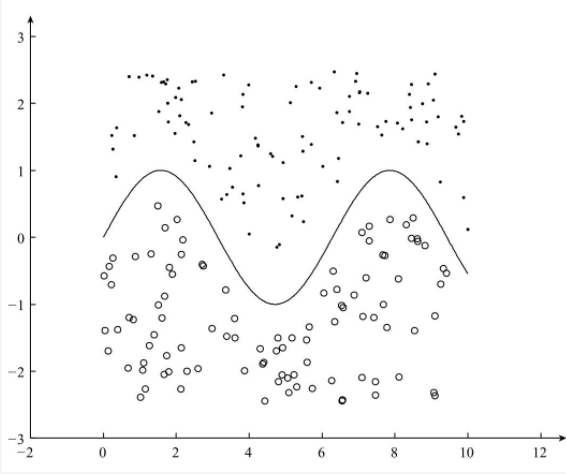
1.2、Logistics Regression模型
Logistics Regression模型为广义的线性模型的一种,属于线性的分类模型。对于线性可分问题,需要找到一条直线,能够将两个不同的类分开,这条直线也称为超平面。对于上述超平面,可以使用如下的线性函数表示:
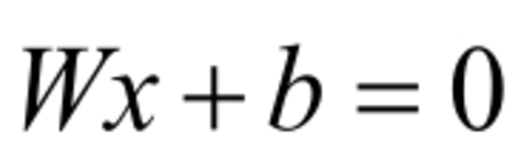
其中W为权重,b为偏置。若在多维的情况下,权重W和偏置b均为向量。在Logistic Regression算法中,通过对训练样本的学习,最终得到该超平面,将数据分成正负两个类别。此时可以使用阈值函数,将样本映射到不同的类别中,常见的阈值函数有Sigmoid函数,其形式如下:

Sigmoid函数的图像如图所示。

从Sigmoid函数的图像可以看出,其函数值域为(0,1),在0附近的变化比较明显。其导函数 为:
为:

以下为Python实现Sigmoid函数,为了能够使用numpy中的函数,我们首先导入numpy
# -*- coding: UTF-8 -*-
# date:2018/5/24
# User:WangHong
import numpy as np
def sig(x):
'''
name:Sigmoid函数
:param x:
:return:Sigmoid函数的值
'''
return 1.0 / (1 + np.exp(-x))
下列代码绘制自变量取值在[-7,7]的Sigmoid函数图像:
# -*- coding: UTF-8 -*-
# date:2018/5/24
# User:WangHong
import numpy as np
import matplotlib.pyplot as plt
def sig(x):
'''
name:Sigmoid函数
:param x:
:return:Sigmoid函数的值
'''
return 1.0 / (1 + np.exp(-x))
z = np.arange(-7,7,0.1)
phi_z = sig(z)
plt.plot(z,phi_z)
plt.axvline(0.0,color='k')
plt.axhspan(0.0,1.0,facecolor='1.0',alpha=1.0,ls='dotted')
plt.axhline(y=0.0,ls='dotted',color='k')
plt.axhline(y=0.5,ls='dotted',color='k')
plt.axhline(y=1.0,ls='dotted',color='k')
plt.yticks([0.0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0])
plt.ylim(-0.1,1.1)
plt.xlabel('z')
plt.ylabel('$phi (z)$')
plt.show()

可以看出,sigmoid函数连续,光滑,严格单调,以(0,0.5)中心对称,是一个非常良好的阈值函数。
当x趋近负无穷时,y趋近于0;趋近于正无穷时,y趋近于1;x=0时,y=0.5。当然,在x超出[-6,6]的范围后,函数值基本上没有变化,值非常接近,在应用中一般不考虑。
Sigmoid函数的值域范围限制在(0,1)之间,我们知道[0,1]与概率值的范围是相对应的,这样sigmoid函数就能与一个概率分布联系起来了。
Sigmoid函数的导数是其本身的函数,即f ′ (x)=f(x)(1−f(x)) ,
计算非常方便,也非常节省计算时间。推导过程如下:

在程序中,Sigmoid函数的输出为Simoid值,对于输入向量X,其属于正例的概率为:
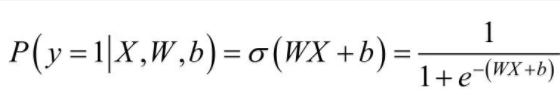
其中, 表示的是Sigmoid函数。那么,对于输入向量X,其属于负例的概率为:
表示的是Sigmoid函数。那么,对于输入向量X,其属于负例的概率为:
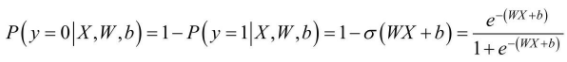
对于Logistics Regression算法来说,需要求解的分隔超平面中的参数,即为权重矩阵W和偏置向量b,那么这些参数该如何求解呐?为了求解模型的两个参数,首先必须定义损失函数。
1.3、损失函数
对于上述的Logistics Regression算法,其属于类别y的概率为:
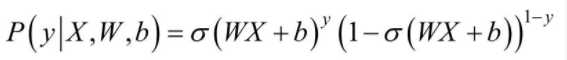
要求上述问题的参数W和b,可以使用极大似然法对其进行估计,假设训练数据集有m个训练样本{(X1,y1),(X2,y2),....,(Xm,ym)},则其似然函数为:

其中,假设函数hw,b(X(i))为:

对于似然函数的极大值的求解,通常使用Log似然函数,在Logistics Regression算法中,通常是将负的Log似然函数作为其损失函数,即the negative log-likelihoo(NLL)作为其损失函数,此时,需要计算的NLL的最小值。损失函数lW,b为:

此时,我们需要求解的问题为:

为了求解德损失函数lW,b的最小值,可以使用基于梯度的方法进行求解。
1.4、梯度下降法:
在机器学习算法中,对于很多监督学习模型,需要对原始的模型构建损失函数,接下来便是通过优化算法对损失函数进行优化,以便寻找到最优的参数W,字求解机器学习参数W的优化算法时,使用较多的是基于梯度下降的优化算法(Gradient Descent,GD)。
梯度下降法的优点,只需要求解损失函数的一阶导数,计算的成本比较小,这使得梯度下降法能在很多大规模数据集上得到应用。梯度下降法的含义是通过当前点出的梯度方向寻找新的迭代点,并从当前点移动到新的迭代点继续寻找新的迭代点,直到找到最优解。
1.4.1、梯度下降法的流程
梯度下降法是一种迭代性的优化算法,根据初始点在每一次迭代的过程中选择下降的方向,静儿改变需要修改的参数,对于优化问题min f(W),梯度下降法的详细过程如下所示:
-
-
- 随机选择一个初始点W0
- 重复以下过程

- 决定梯度下降方向:
- 选择步长α
- 更新:Wi+1=Wi+α*di
- 直到满足终止条件。
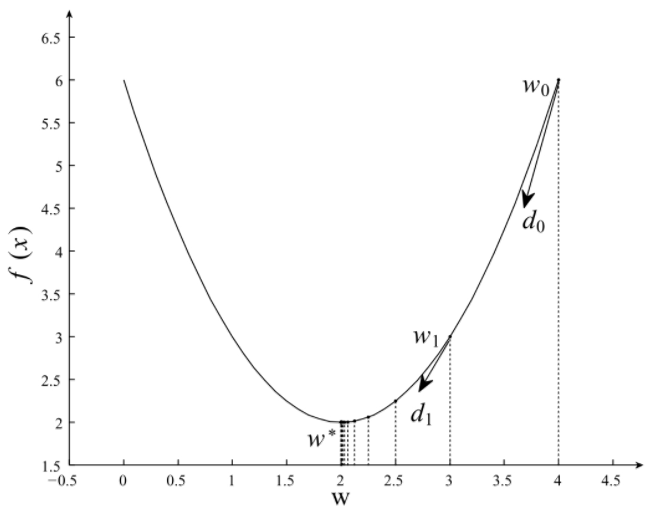
-
在初始时,在 W0处,选择下降的方向d0,选择步长α,更新W的值,此时到达W1处,判断是否满是终止条件,发现并未到达最优解W*,重复上述的过程,直至到达W*
1.5、凸优化与非凸优化
简单来讲,凸优化问题是指只存在一个最优解的优化问题,即在任何一个局部最优解即全局最优解,如图所示:

非凸优化是指在解空间存在多个局部最优解,而全局最优解是其中的某一个局部最优解,如图
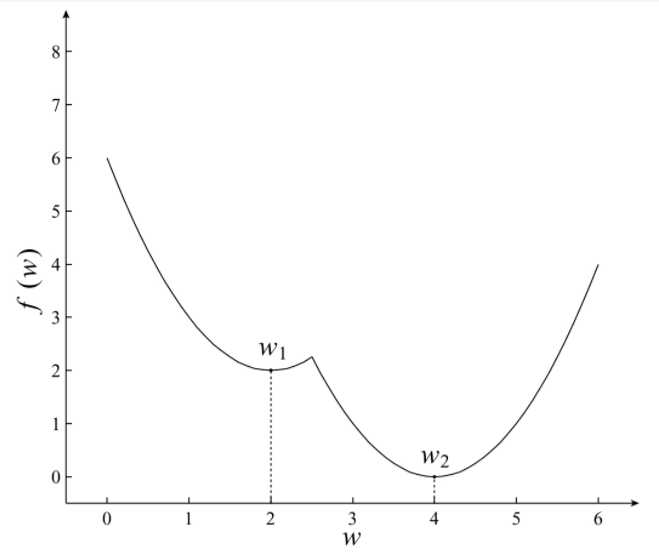
最小二程(Least Sqares)、岭回归(Ridge Regression)和Logistics回归(Logistics Regression)的损失函数都是凸优化问题。
1.6、利用梯度下降法训练Logistics Regression模型
对于上述的Logistics Regression算法的损失函数可以通过梯度下降法对其进行求解,其梯度为:
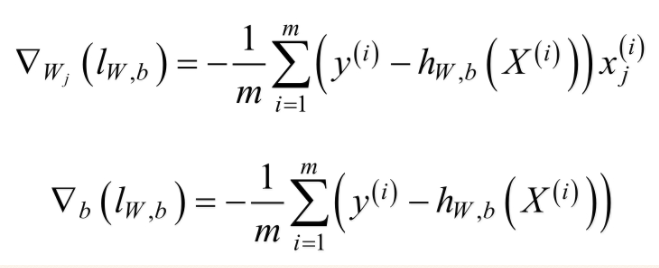
其中xj(i)表示的是样本X(i)的第j个分量。取w0=b,且将偏置项的变量x0设置为1,则可以将上述的梯度合并为:

根据梯度下降法,得到如下更新公式:
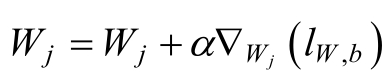
利用上述的Logistics Regression中的权重的更新公式,可以实现Logistics Regression模型的训练,下面是利用梯度下降法训练的具体过程,程序如下:
def lr_train_bgd(feature,label,maxCycle,alpha):
'''
:param feature: 特征
:param label: 标签
:param maxCycle: 最大迭代次数
:param alpha: 学习率
:return w:权重
'''
n = np.shape(feature)[1] #特征个数
w = np.mat(np.ones((n,1)))#初始化权重
i = 0
while i<=maxCycle:#在最大迭代次数的范围内
i += 1#当前的跌打次数
h = sig(feature*w) #计算Sigmoid值
err = label - h
if i%100==0:
print(" ----------iter="+str(i)+
",train error rate="+str(error_rate(h,label)))
w = w+alpha*feature.T*err#修正权重
return w
误差函数为:
def error_rate(h,label):
'''
计算当前的损失函数值
:param h: 预测值
:param label: 实际值
:returnsum_ree / m: 错误率
'''
m = np.shape(h)(0)
sum_err = 0.0
for i in range(m):
if h[i,0]>0 and (1 - h[i,0])>0:
sum_err -= (label[i,0]*np.log(h[i,0]) +
(1-label[i,0]) * np.log(1-h[i,0]))
else:
sum_err -= 0
return sum_err / m
1.7梯度下降法的若干问题
1.为了求解优化问题f(w)的最小值,我们希望每次迭代的结果能够接近最优值W*,对于一维的情况,如图所示:
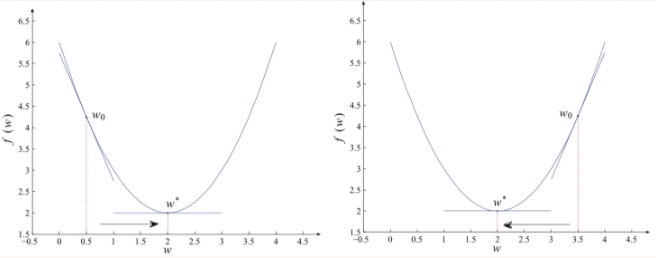
若当前的梯度为负,则最小值在当前点的右侧,若当前点的梯度为正,则最小值在当前点的左侧,负的梯度即为下降的方向。对于上述的一维的情况,有下述的更新规则:
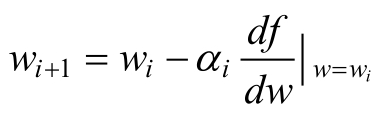
其中,αi为步长。对于二维的情况,此时更新的规则如下:
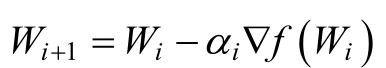
▽代表的含义是矢量求偏导
2.步长的选择:
对于步长的选择,若选择太小,会导致收敛速度比较慢,若选择较大,则会出现震荡的现象,即跳过最优解,在最优解附近徘徊,如图:

步长选择过大 步长选择过小
因此,选择合适的步长对于梯度下降的收敛效果显得尤为重要,如图:
