20162321-王彪-实验四总结

写在前面：程序设计与数据结构到目前为止的大题成绩出来了，悄悄咪咪地看了一下，发现实验得分和实验博客得分都不高，说实话有点尴尬。可能是在提交实验作业时过于简单，提交不完全，而实验博客也不是太详细，导致分数不高。所以这最后一次实验博客，一定要仔细并且详尽讲述本次实验的理解和思路历程。

实验四-图的实现与应用-1

用邻接矩阵实现无向图（边和顶点都要保存），实现在包含添加和删除结点的方法，添加和删除边的方法，size(),isEmpty()，广度优先迭代器，深度优先迭代器，给出伪代码，产品代码，测试代码（不少于5条测试），上方提交代码链接，附件提交测试截图

邻接矩阵

• 用二维数组来实现矩阵，邻接矩阵的长度等于顶点个数，邻接矩阵（A，B），其中A，B表示的是顶点在顶点集合中的位置。而邻接矩阵（二维数组）的每个位置则表示图的边（带权图：每个位置存入数字代表权值，没有边则用-1或0；非带权图：每个位置存入布尔值来表示两个顶点是否连接）
• 无向图和有向图的邻接矩阵：
  无向图和有向图的邻接矩阵有着些许差别（我们以顶点：Ａ，Ｂ，Ｃ，Ｄ，Ｅ为例）
  

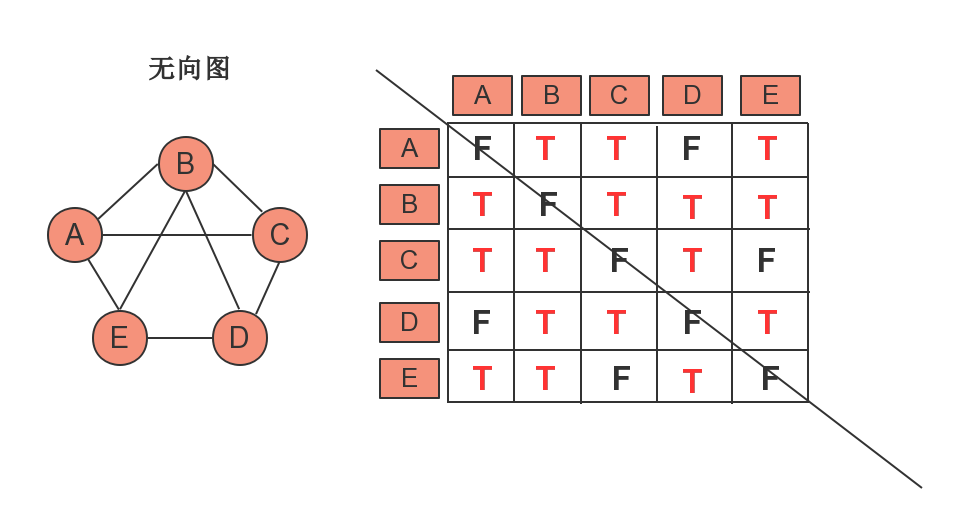
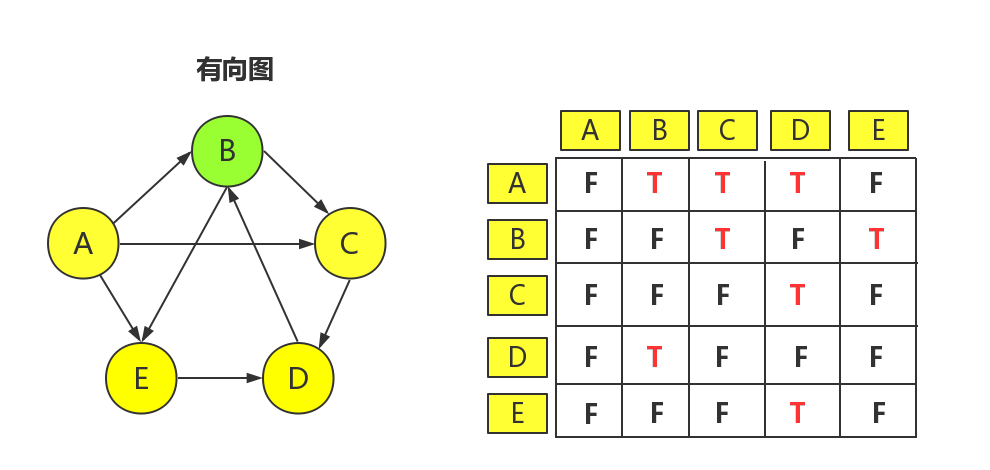
我们可以看到无向图的邻接矩阵是对称，这是因为在无向图中（Ａ，Ｂ）所代表的边的含义与（Ｂ，Ａ）所代表的边的含义完全一样，而有向图则不同。

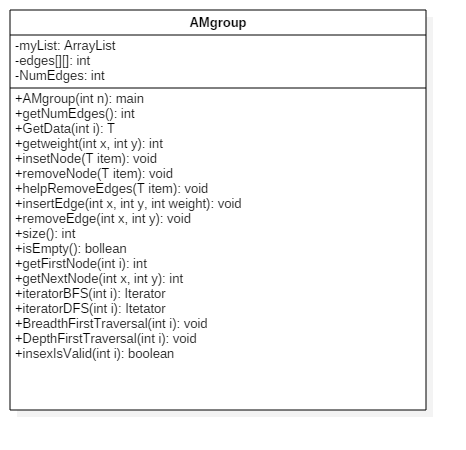
UML类图

伪代码

    属性{
        链表（保存顶点）
        二维数组（邻接矩阵）
        边的数量
} 
   构造函数（int n）{
        根据n来初始化链表和二维数组
}
    插入顶点（T item）{
        链表中加入item
}
    插入边（int x，int y,int weight）{
        二维数组[x][y] = weight;
        边的数量增加
}
    删除边（intx ,int y）{
        二维数组[x][y] = 0 or -1
        边的数量减少
}
    删除顶点（T item）{
        调用帮助删除边函数
        顶点链表移除item
}
    帮助删除边（T item）{
        得到item在顶点链表中位置
        新建二维数组，n1 = 原二维数组长度-1
        for(int i=0;i<原二维数组长度;i++){
            如果 i = item的位置，则继续循环
            如果 i < item的位置，则建立循环（int j=0;j<n;j++）{
                    如果j=item的位置，则继续循环；
                    如果j<item的位置，则新数组（i,j）位置上的值=原数组（i,j）位置上的值；
                    如果j>item的位置，则新数组（i,j-1）位置上的值 = 原数组(i,j)位置上的值；
        }
            如果i > item的位置，则建立循环（int j=0;j<n;j++）{
                    如果j=item的位置，则继续循环
                    如果j<item的位置，则新数组(i-1,j)位置上的值=原数组(i,j)位置上的值；
                    如果j>item的位置，则新数组(i-1,j-1)位置上的值=原数组(i,j)位置上的值；
        }
        将新数组指向原数组
    }    

    是否为空{
        如果顶点表的长度为0，则返回正确；
    }
}

• 关于深度优先和广度优先遍历的实现

书上给了两个方法，但由于只是片面的给了单独的方法，所以以下是我对书中的代码的注释和改动。

    public Iterator<T> iteratorBFS(int startIndex){
        //用来保存从队列中出队的数，此数是要加入迭代器中的顶点在顶点集中的下标
        int currentVertex;
        //该队列用来存储顶点在顶点集中的位置
        LinkedQueue<Integer> traversalQueue = new LinkedQueue<>();
        //该迭代器保存的是顶点元素
        ArrayIterator<T> iter = new ArrayIterator<>();
        /* insexIsValid(int n)
        ** 书中并没有给出indexIsValid的具体实现方式
        ** 根据命名推断：index是否有效，所以该方法的目的是判断参数startIndex是否是有效值
        **public  boolean insexIsValid(int index){
        **        if (0<index&&index<myList.size()){
        **                return true;
        **        }
        **        else return false;
        **    }  
        */           
        if (!indexIsValid(startIndex))
            return iter;
        //visited数组帮助判断顶点是否被访问
        boolean[] visited = new boolean[myList.size()];
        //利用循环现将visited全部标记为未访问
        for (int vertexIndex=0;vertexIndex<myList.size();vertexIndex++){
            visited[vertexIndex]= false;
        }
        //初始化操作：将参数startIndex入队，并标记为已访问
        traversalQueue.enqueue(startIndex);
        visited[startIndex] =  true;
        //while循环，只要队列不为空就继续循环
        while (!traversalQueue.isEmpty()){
           
            //将队列中第一个元素出队，赋值给currentVertex
           
            currentVertex = traversalQueue.dequeue();
            //迭代器加入顶点集中currentVertex位置的元素
            iter.add(myList.get(currentVertex));
            //利用循环遍历与currentVertex位置的顶点相连的所以顶点
            for (int vertexIndex=0;vertexIndex<myList.size();vertexIndex++){
                if (edges[currentVertex][vertexIndex]>0&&!visited[vertexIndex]){
                    traversalQueue.enqueue(vertexIndex);
                    visited[vertexIndex] = true;
                }
            }
        }
        return iter;
    }

实验一：代码

实验四-图的实现与应用-2

用十字链表实现无向图（边和顶点都要保存），实现在包含添加和删除结点的方法，添加和删除边的方法，size(),isEmpty()，广度优先迭代器，深度优先迭代器，给出伪代码，产品代码，测试代码（不少于5条测试），上方提交代码链接，附件提交测试截图

十字链表

• 实验二是比较难的，原因就在于上课时老师对十字链表的讲述也不是很详细，自身对十字链表的理解也不够。导致在上手时完全不知道该怎么做，网上查找了很多资料，一开始也是有点云里雾里的。

• 十字链表比较难理解的地方是在于十字这一概念：十字链表是为了便于求得图中顶点的度（出度和入度）而提出来的。它是综合邻接表和逆邻接表形式的一种链式存储结构。

• 既然是链表那么就得构建结点类，十字链表中有有两种结点结构：边结点结构，顶点结构

• 顶点结构
  

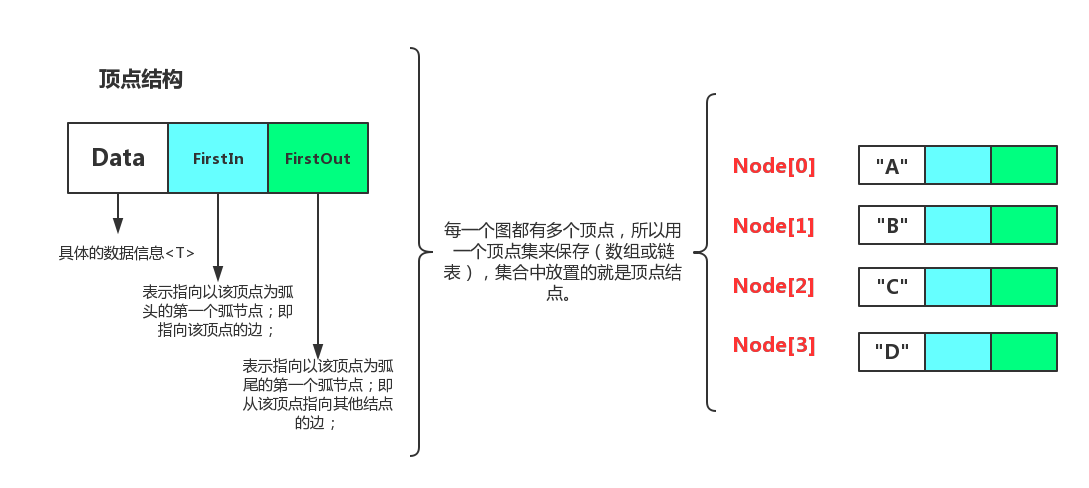
• 弧结构
  

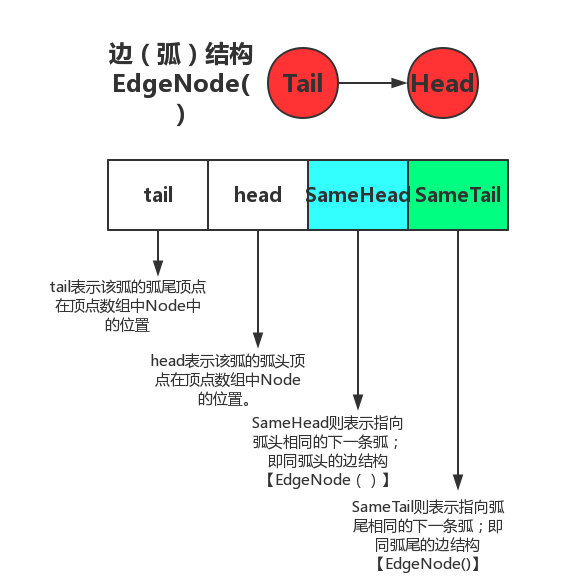
• 接下来，就要弄清楚十字链表的具体实现，以下是我用ProcessOn画的理解图，本博客中所有图就出自于我的ProcessOn
  

• 我个人理解为：每个顶点结点都有两个链表，正如上图的蓝色和绿色标记的，以结点B为例：蓝色的链表表示以B为弧尾的边的集合即进入B的边的集合；绿色的链表表示以B为弧头的边的集合（从B出去的边）

UML类图

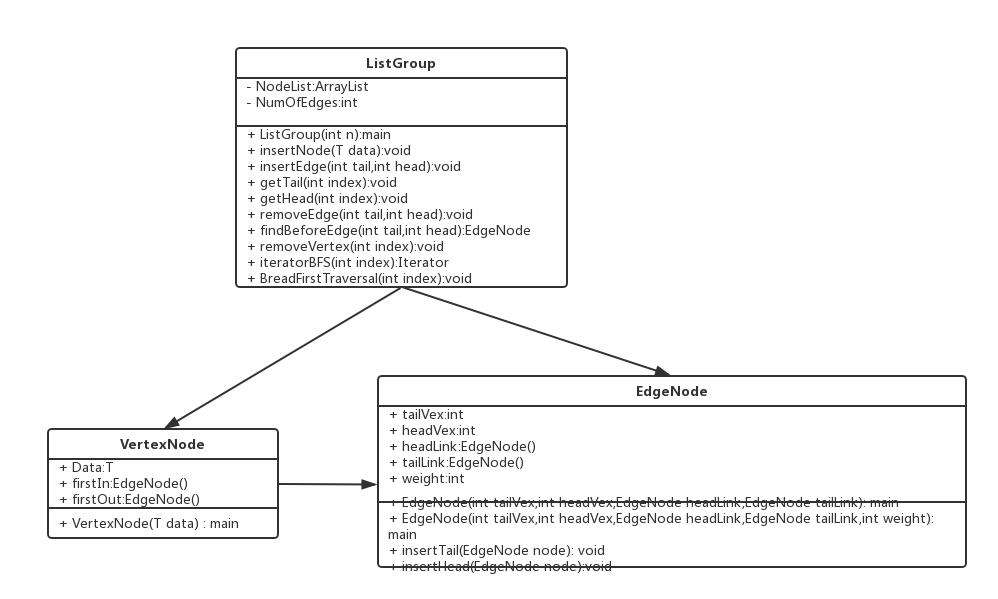
代码解析

• 插入边:insertEdge(int tail,int head)，结合前面的图我们知道，如果要插入一条边，那么这条边对应的头结点的FirstIn表就得加入此条边，同时这条边对应的尾节点的FirstOut表就得也得加入此条边。
  

public void insertEdge(int tail,int head){
        EdgeNode<T> myEdge = new EdgeNode(tail,head,null,null);
        VertexNode<T> tailNode = NodeList.get(tail);
        VertexNode<T> headNode = NodeList.get(head);
        if (tailNode.firstOut==null){
            tailNode.firstOut = myEdge;
        }
        else {
            tailNode.firstOut.insertTail(myEdge);
        }
        if (headNode.firstIn==null){
            headNode.firstIn = myEdge;
        }
        else {
           headNode.firstIn.insertHead(myEdge);
        }
    }

• 删除边

public void removeEdge(int tail,int head){
            EdgeNode myEdge = NodeList.get(tail).firstOut;
            if (myEdge.tailVex==tail&&myEdge.headVex==head){
                if (!(myEdge.tailLink==null&&myEdge.headLink==null)){
                    NodeList.get(tail).firstOut = myEdge.tailLink;
                }
                else NodeList.get(tail).firstOut=null;
            }
            else {
                myEdge = findBeforeEdge(tail,head);
                myEdge.tailLink = null;
            }
    }
public EdgeNode findBeforeEdge(int tail,int head){
        EdgeNode myEdge = null;
        if (NodeList.get(tail).firstOut!=null){
             myEdge = NodeList.get(tail).firstOut;
        }
        else return null;
        while (myEdge.tailLink!=null){
            if (!(myEdge.tailLink.tailVex==tail&&myEdge.tailLink.headVex==head)) {
                myEdge = myEdge.tailLink;
            }
            else
                break;
        }
        return myEdge;
    }

实验二：代码

实验四-图的实现与应用-3

实现PP19.9,给出伪代码，产品代码，测试代码（不少于5条测试）,上方提交代码链接,附件提交测试截图

PP19.9

创建计算机网络路由系统，输入网络中点到点的线路，以及每条线路使用的费用，系统输出网络中各点之间最便宜的路径，指出不相通的所有位置

• 主要实现原理就是查找两个顶点之间的最短路径；其余实现则没有区别，具体是带权的无向图

关键代码

public void vertexShortestDist(){
        for (int i=0;i<myList.size();i++){
                helpShortestDist(i);
        }
    }
    public void helpShortestDist(int index){
        for (int i=0;i<myList.size();i++){
            for (int j=0;j<myList.size();j++){
                if (edges[i][index]!=0&&edges[index][j]!=0){
                    if (edges[i][j]==0){
                    edges[i][j]=edges[i][index]+edges[index][j];}
                    else if (edges[i][j]>edges[i][index]+edges[index][j])
                        edges[i][j]=edges[i][index]+edges[index][j];
                }
            }
        }
    }

• 这里一次以每个顶点为中间点对整个二维数组进行加工，但关键是每次添加一条边时都调用此方法。
• 该代码的伪代码来自于蓝墨云班课上的PPT163：各顶点对间最短路径算法，略有不同的是：初始化矩阵的方式不同，PPT中直接出示话了矩阵，而我的做法则是在添加边时调用函数，致使每次添加边后，矩阵都会变化，使其始终保持储存最小路径

public void inserEdge(int a,int b,int weigth){
        if (!insexIsValid(a)||!insexIsValid(b)){
            throw new NumberFormatException("Wrong number");
        }
        edges[a][b] = weigth;
        vertexShortestDist();
        NumEdges++;
    }

• 实现原理很简单：例如以A为中间点，判断BC之间的路径时，比较Node[B][C]?Node[B][A]+Node[A][C]的大小关系，若<和=则Node[B][C]的值不做更改，反之Node[B][C]=Node[B][A]+Node[A][C]

实验三：代码