机器学习十讲第三讲

分类

分类是另一种典型的有监督学习问题。标签（模型预测值）y为离散值

感知机

• 找到一条直线，将两类数据分开。当出现划分错误情况（如正值在左/负值在右），就需要进行优化，优化目标简单的说就是让划分错误的那个点尽可能地离直线近，即距离越小。

• 优化目标

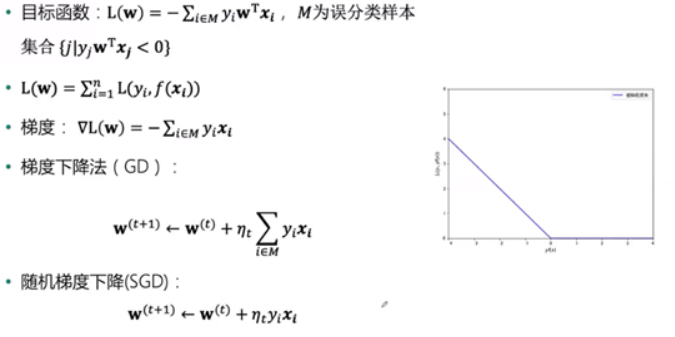
• 代码实现

def perception(X,y,learning_rate,max_iter=1000):
    w = pd.Series(data=np.zeros_like(X.iloc[0]),index=X.columns) # 初始化参数 w0
    W = [w] # 定义一个列表存放每次迭代的参数
    mis_samples = [] # 存放每次误分类的样本
    
    for t in range(max_iter):
        
        # 2.1 寻找误分类集合 M
        m = (X.dot(w))*y #yw^Tx < 0 的样本为误分类样本
        X_m = X[m <= 0]  # 误分类样本的特征数据
        y_m = y[m <= 0]  # 误分类样本的标签数据
        
        if(len(X_m) > 0): # 如果有误分类样本，则更新参数；如果不再有误分类样本，则训练完毕。
            # 2.2 从 M 中随机选取一个样本 i 
            i = np.random.randint(len(X_m))
            mis_samples.append(X_m.iloc[i,:])
            # 2.3 更新参数 w 
            w = w + learning_rate * y_m.iloc[i]*X_m.iloc[i,:]
            W.append(w)
        else: 
            break
            
    mis_samples.append(pd.Series(data=np.zeros_like(X.iloc[0]),index=X.columns))
    return w,W,mis_samples
    
    w_percept,W,mis_samples = perception(data[["x1","x2","ones"]], 		 data["label"],1,max_iter=1000)
    
   #将学习到的感知机的决策直线可视化，观察分类效果。
   x1 = np.linspace(-6, 6, 50)
   x2 = - (w_percept[0]/w_percept[1])*x1 - w_percept[2]/w_percept[1]

plt.figure(figsize=(8, 8)) #设置图片尺寸

plt.scatter(data_pos["x1"],data_pos["x2"],c="#E4007F",marker="^") # 类别为1的数据绘制成洋红色
plt.scatter(data_neg["x1"],data_neg["x2"],c="#007979",marker="o") # 类别为-1的数据绘制成深绿色
plt.plot(x1,x2,c="gray") # 画出分类直线

plt.xlabel("$x_1$") #设置横轴标签
plt.ylabel("$x_2$") #设置纵轴标签
plt.title('手动实现的感知机模型')
plt.xlim(-6,6) #设置横轴显示范围
plt.ylim(1,5) #设置纵轴显示范围
plt.show()

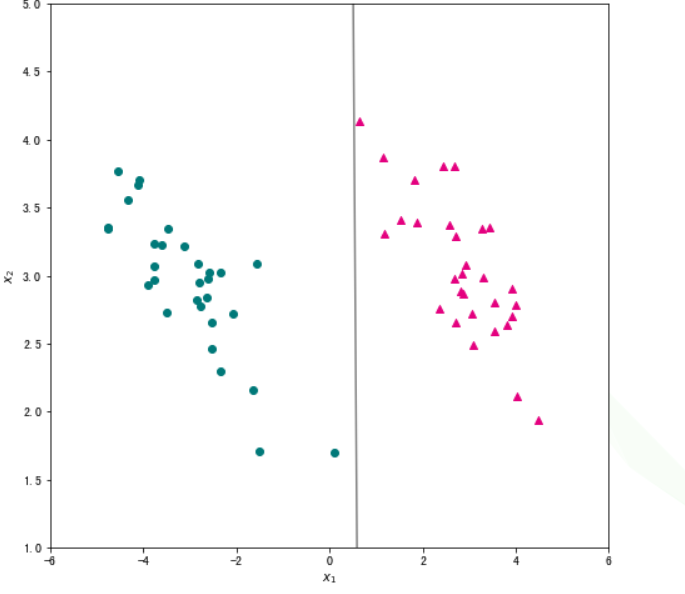
支持向量机

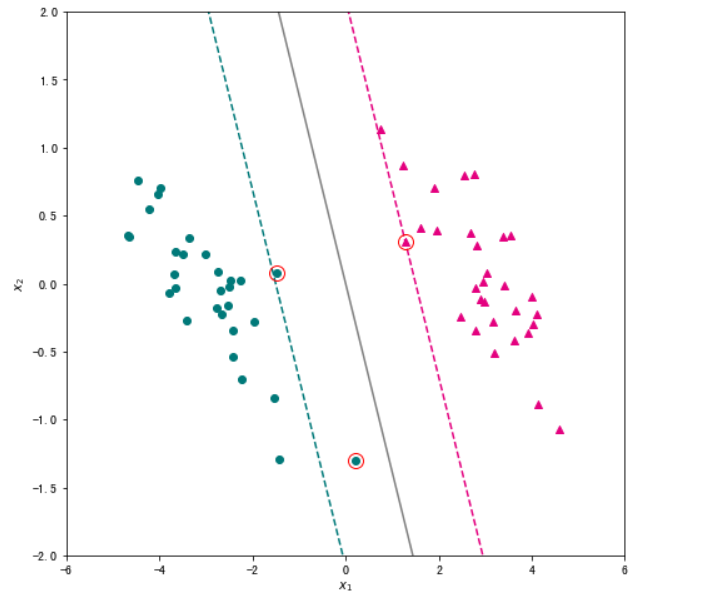
• 找到一条直线，不仅将两类数据正确分类，还使得数据离直线尽量远
• 间隔最大化

• 样本损失函数：

• 优化目标

  

• 代码实现

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# 定义函数
def linear_svm(X,y,lam,max_iter=2000):  
    w = np.zeros(X.shape[1]) # 初始化w
    support_vectors = [] # 创建空列表保存支持向量
    
    for t in range(max_iter): # 进行迭代
        
        learning_rate = 1/(lam * (t + 1)) # 计算本轮迭代的学习率
        i = np.random.randint(len(X)) # 从训练集中随机抽取一个样本
        ywx = w.T.dot(X.values[i])*y[i]  # 计算y_i w^T x_i
        
        if ywx < 1:# 进行指示函数的判断
            w = w - learning_rate * lam*w + learning_rate * y[i] * X.values[i] # 更新参数       
        else:
            w = w - learning_rate * lam*w # 更新参数
    for i in range(len(X)):
        ywx = w.T.dot(X.values[i])*y[i]  # 计算y_i w^T x_i
        if ywx <= 1: # 根据样本是否位于间隔附近判断是否为支持向量
            support_vectors.append(X.values[i])
    
    return w,support_vectors


# 对训练集数据进行归一化，则模型无需再计算截距项
X = data[["x1","x2"]].apply(lambda x: x - x.mean())
# 训练集标签
y = data["label"]
w,support_vectors = linear_svm(X,y, lam=0.05, max_iter=5000)


# 创建绘图框
plt.figure(figsize=(8, 8))
# 绘制两类样本点
X_pos = X[ y==1 ]
X_neg = X[ y==-1 ]
plt.scatter(X_pos["x1"],X_pos["x2"],c="#E4007F",marker="^") # 类别为1的数据绘制成洋红色
plt.scatter(X_neg["x1"],X_neg["x2"],c="#007979",marker="o") # 类别为-1的数据绘制成深绿色

# 绘制超平面
x1 = np.linspace(-6, 6, 50)
x2 = - w[0]*x1/w[1]
plt.plot(x1,x2,c="gray")

# 绘制两个间隔超平面
plt.plot(x1,-(w[0]*x1+1)/w[1],"--",c="#007979")
plt.plot(x1,-(w[0]*x1-1)/w[1],"--",c="#E4007F")

# 标注支持向量
for x in support_vectors:
    plt.plot(x[0],x[1],"ro", linewidth=2, markersize=12,markerfacecolor='none')
    
# 添加轴标签和限制轴范围
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")
plt.xlim(-6,6)
plt.ylim(-2,2)

逻辑回归

• 找到一条直线使得观察到训练集的“可能性”最大。数据离直线越远越接近于1，反之则趋近于0
• 赋予样本概率

• 似然函数与负对数似然函数

• 代码实现

import numpy as np
# 定义梯度下降法求解的迭代公式
def logistic_regression(X,y,learning_rate,max_iter=1000):
    # 初始化w
    w = np.zeros(X.shape[1])
    for t in range(max_iter):      
        # 计算yX
        yx = y.values.reshape((len(y),1)) * X 
        # 计算1 + e^(yXW)
        logywx = (1 +  np.power(np.e,X.dot(w)*y)).values.reshape(len(y),1) 
        w_grad = np.divide(yx,logywx).sum()
        # 迭代w
        w = w + learning_rate * w_grad    
    return w


# 输出训练好的参数
w = logistic_regression(data[["x1","x2","ones"]], data["label"],0.5,max_iter=1000)  
print(w)

# 可视化分类结果
x1 = np.linspace(-6, 6, 50)
x2 = - (w[0]/w[1])*x1 - w[2]/w[1]

plt.figure(figsize=(8, 8))
plt.scatter(data_pos["x1"],data_pos["x2"],c="#E4007F",marker="^") # 类别为1的数据绘制成洋红色
plt.scatter(data_neg["x1"],data_neg["x2"],c="#007979",marker="o") # 类别为-1的数据绘制成深绿色
plt.plot(x1,x2,c="gray")

plt.xlabel("$x_1$")
plt.ylabel("$x_2$")
plt.xlim(-6,6)
plt.ylim(1,5)
plt.show()

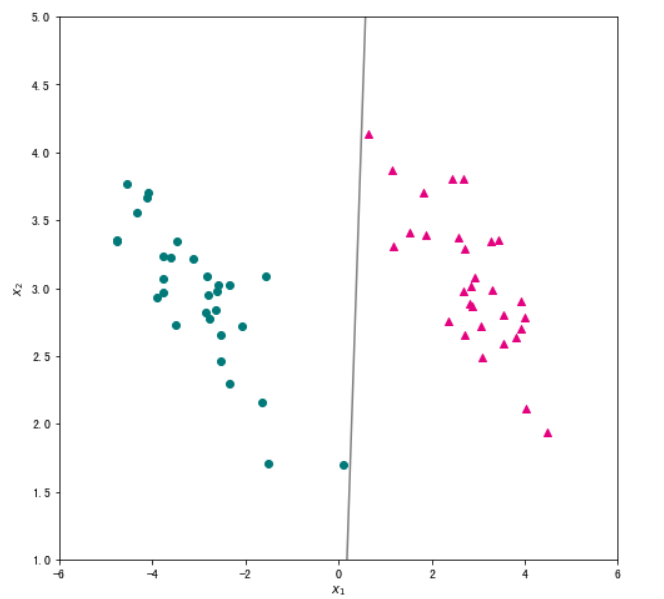
• 我们也可以采用随机梯度下降求解逻辑回归

# 定义随机梯度下降法求解的迭代公式
def logistic_regression_sgd(X,y, learning_rate, max_iter=1000): 
    # 初始化w
    w = np.zeros(X.shape[1])
    for t in range(max_iter):
        # 随机选择一个样本
        i = np.random.randint(len(X))
        # 计算yx
        yixi = y[i] * X.values[i]
         # 计算1 + e^(yxW)
        logyiwxi = 1 +  np.power(np.e, w.T.dot(X.values[i])*y[i])
        w_grad = yixi / logyiwxi
        
        # 迭代w
        w = w + learning_rate * w_grad  
        
    return w

# 输出训练好的参数
w = logistic_regression_sgd(data[["x1","x2","ones"]], data["label"],0.5,max_iter=1000)  
print(w)

# 可视化分类结果
x1 = np.linspace(-6, 6, 50)
x2 = - (w[0]/w[1])*x1 - w[2]/w[1]

plt.figure(figsize=(8, 8))
plt.scatter(data_pos["x1"],data_pos["x2"],c="#E4007F",marker="^") # 类别为1的数据绘制成洋红色
plt.scatter(data_neg["x1"],data_neg["x2"],c="#007979",marker="o") # 类别为-1的数据绘制成深绿色
plt.plot(x1,x2,c="gray")

plt.xlabel("$x_1$")
plt.ylabel("$x_2$")
plt.xlim(-6,6)
plt.ylim(1,5)
plt.show()

新闻文本分类案例

#读取新闻数据并显示前五行
raw_train = pd.read_csv("./input/chinese_news_cutted_train_utf8.csv",sep="	",encoding="utf8")
raw_test = pd.read_csv("./input/chinese_news_cutted_test_utf8.csv",sep="	",encoding="utf8")
#raw_train.head()

#这里仅进行二分类，选择主题为科技和文化的新闻
raw_train_binary = raw_train[((raw_train["分类"] == "科技") | (raw_train["分类"] == "文化"))]
raw_test_binary = raw_test[((raw_test["分类"] == "科技") | (raw_test["分类"] == "文化"))]
raw_test_binary.head()

#先加载停用词表，并使用该表去除文本中的停用词
stop_words = []
file = open("./input/stopwords.txt") 
for line in file:
    stop_words.append(line.strip())
file.close()
#之后将文本数据转换为词向量（第二讲内容）
##调用sklearn.feature_extraction.text的CountVectorizer
from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer(stop_words=stop_words)
X_train = vectorizer.fit_transform(raw_train_binary["分词文章"])
X_test = vectorizer.transform(raw_test_binary["分词文章"])
#再调用sklearn中的随机梯度下降分类器——SGDClassifier
##调整loss参数分别构建感知机，逻辑回归和线性支持向量机模型
from sklearn.linear_model import SGDClassifier
###感知机模型——loss="perceptron"
percep_clf = SGDClassifier(loss="perceptron",penalty=None,learning_rate="constant",eta0=1.0,max_iter=1000,random_state=111)
###逻辑回归模型——loss="log"
lr_clf = SGDClassifier(loss="log",penalty=None,learning_rate="constant",eta0=1.0,max_iter=1000,random_state=111)
###线性支持向量机模型——loss="hinge"
lsvm_clf = SGDClassifier(loss="hinge",penalty="l2",alpha=0.0001,learning_rate="constant",eta0=1.0,max_iter=1000,random_state=111)


#训练感知机模型并输出分类正确率
percep_clf.fit(X_train,raw_train_binary["分类"])
round(percep_clf.score(X_test,raw_test_binary["分类"]),2)

#训练逻辑回归模型并输出分类正确率
lr_clf.fit(X_train,raw_train_binary["分类"])
round(lr_clf.score(X_test,raw_test_binary["分类"]),2)

#训练线性支持向量机模型并输出分类正确率
lsvm_clf.fit(X_train,raw_train_binary["分类"])
round(lsvm_clf.score(X_test,raw_test_binary["分类"]),2)

#模型效果评估
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(5,5))
# 设置正常显示中文
sns.set(font='SimHei')
# 绘制热力图
y_svm_pred = lsvm_clf.predict(X_test) # 预测标签
y_test_true = raw_test_binary["分类"] #真实标签
confusion_matrix = confusion_matrix(y_svm_pred,y_test_true)#计算混淆矩阵
ax = sns.heatmap(confusion_matrix,linewidths=.5,cmap="Blues",
                 annot=True, fmt='d',xticklabels=lsvm_clf.classes_, yticklabels=lsvm_clf.classes_)
ax.set_ylabel('真实')
ax.set_xlabel('预测')
ax.xaxis.set_label_position('top') 
ax.xaxis.tick_top()
ax.set_title('混淆矩阵热力图')

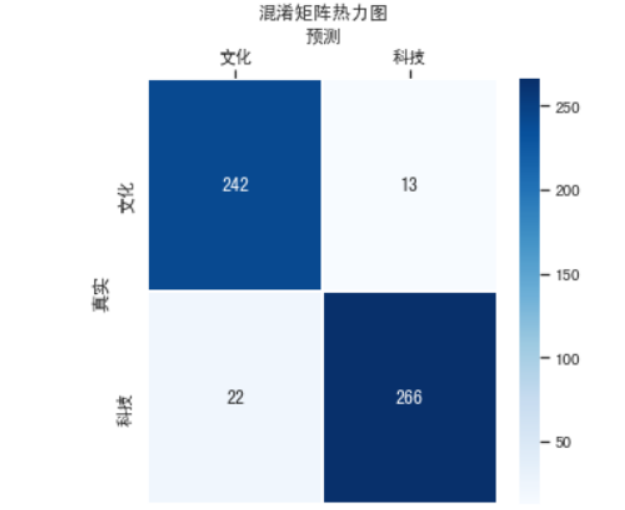
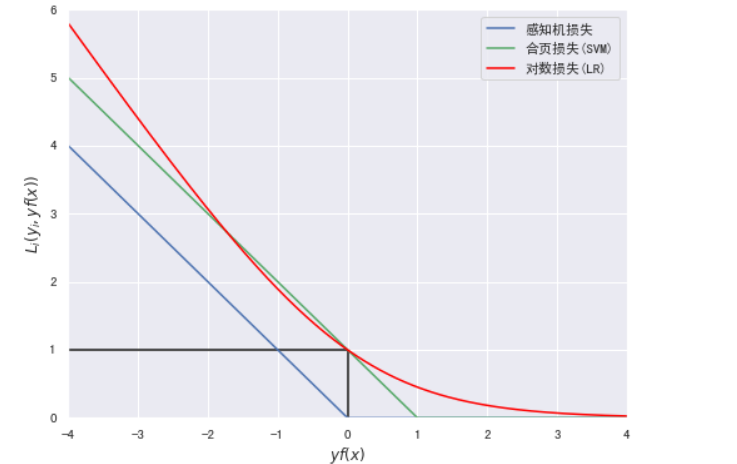
#绘制三种分类模型的损失函数曲线
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
yfx = np.linspace(-4, 4, 500)
perception = [0 if i >= 0 else -i for i in yfx]
hinge = [(1-i) if i <= 1 else 0 for i in yfx]
log = np.log2(1 + np.power(np.e,-yfx))
plt.figure(figsize=(8, 6))
plt.plot(yfx,perception,c="b",label="感知机损失")
plt.plot(yfx,hinge,c="g",label="合页损失(SVM)")
plt.plot(yfx,log,c="red",label="对数损失(LR)")
plt.hlines(1,-4,0)
plt.vlines(0,0,1)
plt.xlabel("$yf(x)$")
plt.ylabel("$L_i(y_i,yf(x))$")
plt.xlim(-4,4)
plt.ylim(0,6)
plt.legend()