14 深度学习-卷积

1.简述人工智能、机器学习和深度学习三者的联系与区别。

2. 全连接神经网络与卷积神经网络的联系与区别。

　　卷积神经网络也是通过一层一层的节点组织起来的。和全连接神经网络一样，卷积神经网络中的每一个节点就是一个神经元。

　　在全连接神经网络中，每相邻两层之间的节点都有边相连，于是会将每一层的全连接层中的节点组织成一列，这样方便显示连接结构。而对于卷积神经网络，相邻两层之间只有部分节点相连，为了展示每一层神经元的维度，一般会将每一层卷积层的节点组织成一个三维矩阵。

　　因此，全连接神经网络和卷积神经网络的唯一区别就是神经网络相邻两层的连接方式。

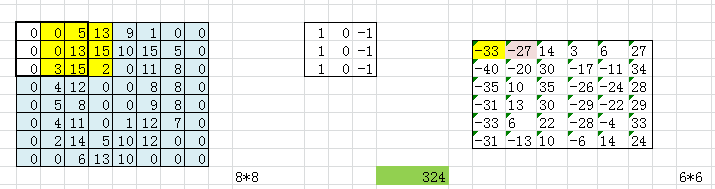
3.理解卷积计算。

以digit0为例，进行手工演算。

from sklearn.datasets import load_digits #小数据集8*8

digits = load_digits()

4.理解卷积如何提取图像特征。

读取一个图像；

以下矩阵为卷积核进行卷积操作；

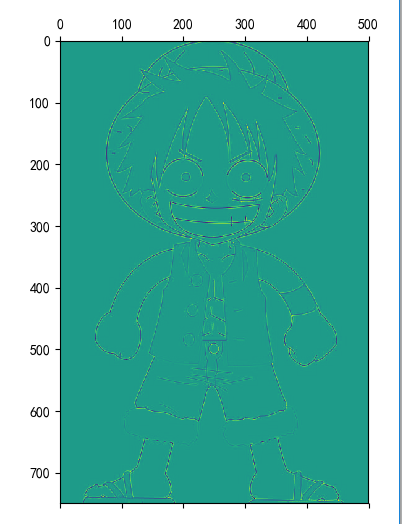
显示卷积之后的图像，观察提取到什么特征。

1	0	-1
1	0	-1
1	0	-1

1	1	1
0	0	0
-1	-1	-1

-1	-1	-1
-1	8	-1
-1	-1	-1

卷积API

scipy.signal.convolve2d

tf.keras.layers.Conv2D

代码：

from PIL import Image
from scipy.signal import convolve2d
import numpy as np
import matplotlib.pyplot as plt

I = Image.open(r'./venv/data/lufei.jpg')
L = I.convert('L')
image = np.array(I)
imageg = np.array(L)

# 卷积矩阵
k = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])
k1 = np.array([[1, 0, -1], [1, 0, -1], [1, 0, -1]])  # 垂直边缘检测
k2 = np.array([[1, 1, 1], [0, 0, 0], [-1, -1, -1]])  # 水平边缘
k3 = np.array([[-1, -1, -1], [-1, 8, -1], [-1, -1, -1]])

# 卷积图像
img0 = convolve2d(imageg, k, boundary='symm', mode='same')
img1 = convolve2d(imageg, k1, boundary='symm', mode='same')
img2 = convolve2d(imageg, k2, boundary='symm', mode='same')
img3 = convolve2d(imageg, k3, boundary='symm', mode='same')

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.title("原图片")
plt.imshow(image)

plt.title("灰度图")
plt.imshow(imageg)
plt.matshow(img0)
plt.matshow(img1)
plt.matshow(img2)
plt.matshow(img3)

结果：

 卷积效果：

 

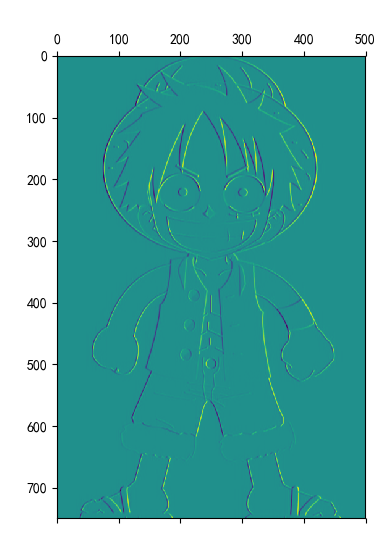
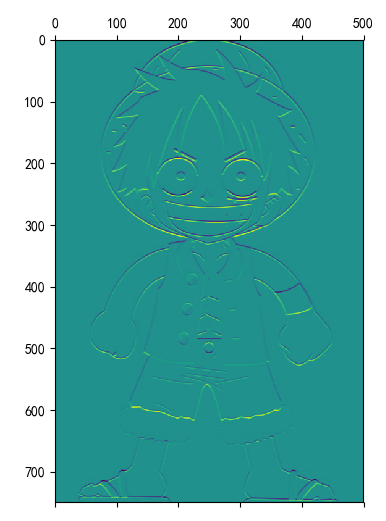
5. 安装Tensorflow,keras