实验二 从角速度到圆周运动 渐开线的再认识
若将螺旋看做是直线运动与圆周运动的叠加,每个旋转周期,直线上移动相同的距离,这样得到的螺旋曲线可以统称为等距螺旋。
当直线与圆周相切,直线速度与圆周速度相同,方向相反时,形成的螺旋即为渐开线螺旋。
【运动形式】
传统的渐开线螺旋描述为:将绕在圆柱上的线条的一头从圆柱上剥离,线头所形成的轨迹即为渐开线螺旋。动画演示如下图所示:

很明显,若用直线运动来描述渐开线,直线一定是与特定的圆周相切的。
上图中采用顺时针的旋转方向,配合从右向左的直线运动,形成了渐开线。
按照常规的理解,上图中的线头是顺时针方向从圆柱中进行剥离,每剥离360°,线头距圆柱的距离增加圆柱的一个周长。
从直线运动的角度来理解:动点(图中的绿色小圈)从直线与圆周的切点出发,逐渐远离切点。该切点(图中的红色小圈)随着圆周在一起旋转,每旋转一个周期,直线上动点移动一个圆周的距离。
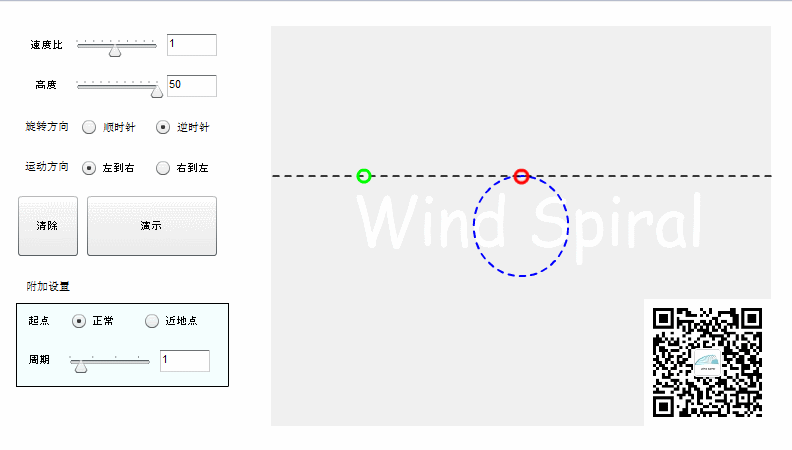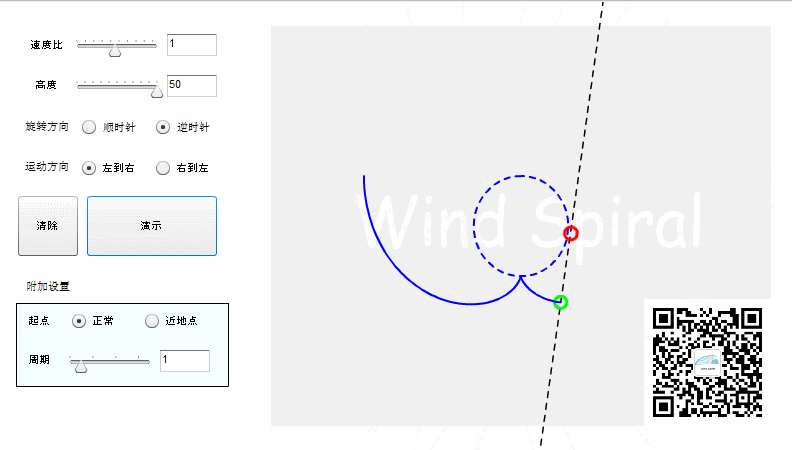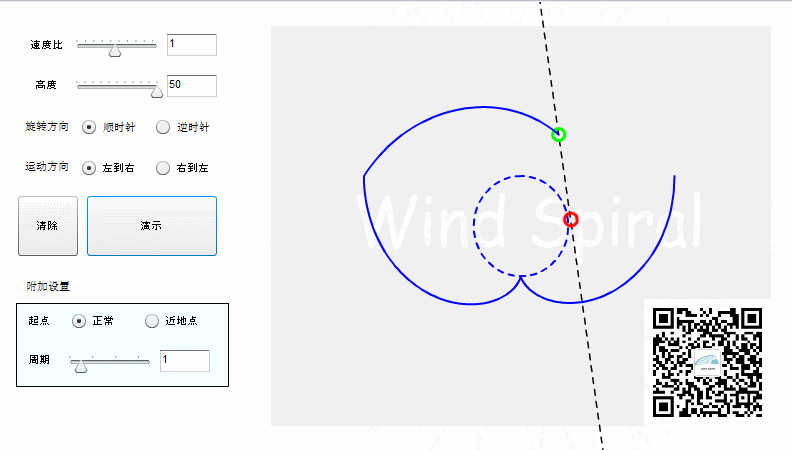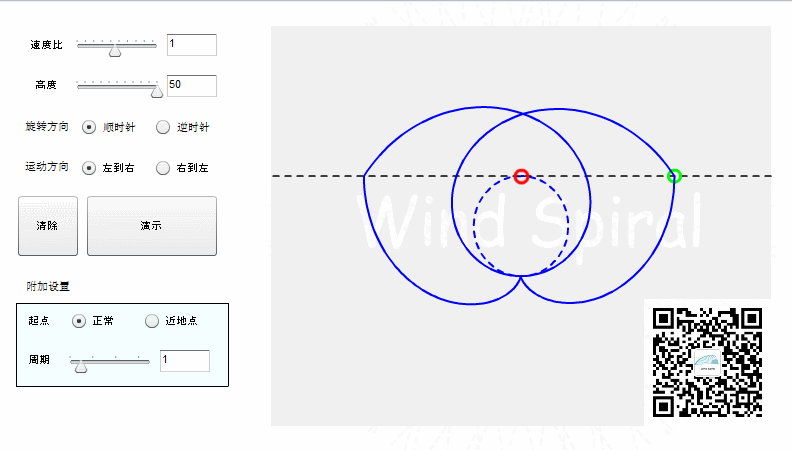
从初始位置的运动方向来看,圆周要顺时针旋转,切点是向右运动。直线上的动点要剥离开,它的运动方向是向左运动。圆周与动点的运动方向相反,速度相同会形成渐开线(运动方式的叠加,并不是速度值的直接叠加)。
若动点与圆周的运动方向相同,尽管切线的位置关系一致、速度关系一致,但形成的螺旋不是渐开线,而是下图的形状。(有没有人和我一样在刚开始画渐开线时,却画出了另外的螺旋?)

上图中,绿点的结束位置不同(运动方向不同),造成螺旋线的形态不同。
与阿基米德螺旋的分析一样,我们并不想止步于传统螺旋的框架内,我们对起点之前的情况更好奇。借助电脑动画技术,我们可以相对容易的画出“完整”的渐开线曲线。

上图的渐开线运动,采用了从左向右的直线运动,圆周运动必须和直线运动相反,因此是逆时针旋转。初始位置的绿色动点 距离 红色切点 为半个圆周的长度,渐开线形成于圆柱的下部。
如果采用从左向右的直线运动,搭配上顺时针的旋转方向则会形成第二种曲线,如下图所示:
从图中可以看到,直线运动与圆周运动的方向,对于螺旋线的形态有着较大的影响,在分析时,是必不可少的先决条件。
【对称特性】
从上面的图形可以看到,渐开线与阿基米德螺旋有所不同的地方在于,当旋转方向不同时,阿基米德螺旋形状完全相同,相切于圆心点,位置相差了180°。对于渐开线来说,不同的旋转方向产生的是不同的两类螺旋,二者相切与圆周上的一点。
【公式分析】
传统的螺旋线分析,通常都是从圆心点出发,按照角速度与直线运动的距离之间的关系进行分析,速度之间的关系并不清晰。
实际上对于特定的圆周,旋转一周的时间可以通过圆周长除以圆周速度得到,若将圆周角用弧度来表示为2Pi,则角速度等于(2*Pi*r/v)/(2*Pi)=r/v。
渐开线剥离的快慢,对螺旋的形状是完全无影响的。因为,在渐开线剥离的过程中,直线运动的速度与圆周运动的速度之比始终为1。在后面的实验中,我们将揭晓等距螺旋的通用公式,通过公式来解释为会么剥离的快慢不会对渐开线的形态造成影响。
======以下属于主观臆测部分======
在我们已知的宇宙世界中,螺旋结构是星体最常见的形式。对于世界起源的主流看法是:世界从一个密度极高的点开始炸裂的。
通过对螺旋运动的观察,我们可以看到,如果直线运动经过圆周运动的叠加,会形成一段收缩的螺旋形态,之后再进入扩散的螺旋形态,这二者是平滑连接的关系。
如果螺旋线在起点之前还可以有一个收缩的过程,那么宇宙是否也是按照某个螺旋线的轨迹先收缩而后扩散呢?
等距螺旋的基础是速度比恒定,当速度比在不断的增大或减小时,螺旋必将呈现加速收缩(或加速发散)的状态。换句话来说,如果,我们的宇宙只是由于旋转的速度在减弱,而直线运动的速度不变,这种情况下,同样可以产生加速扩散的效果。如果这一点可以成立,所谓的暗物质推动宇宙扩散的想法估计就会动摇了吧。
【软件下载】
等距螺旋实验演示软件: