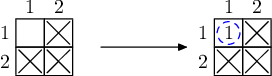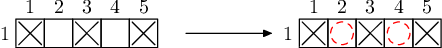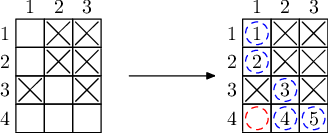有意思的网格图转化。CF Div.1 还是挺有难度的。
注:由于本题有较完美的中文题面,所以不贴英文题面。
英文题面
题目描述
Innopolis 大学的教授正努力研究元素周期表。他们知道,有 (n imes m) 种元素,形成了一个 (n) 行 (m) 列的矩阵。
研究表明,如果元素周期表上有一个元素 A,且元素 B 与它在同一列(A 与 B 不能在同一周期),元素 C 在同一周期(A 与 C 不能在同一列),那么,科学家就可以用这三种元素通过核聚变合成第四种元素 D 的样品,D 与 B 在同一周期,与 C 在同一列。
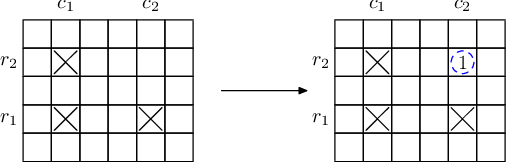
简而言之,如果有在元素周期表中位置为 ((r_1, c_1), (r_1, c_2), (r_2, c_1)) (其中 (r_1 e r_2,c_1 e c_2))的三种元素的样品,就可以生成位置为 ((r_2, c_2))) 的样品。如图所示:
注意:在核聚变中被使用的样品并不会消失,它们可以参与之后的反应;反应得到的样品也可以参与反应。
他们已经获得了 (q) 种元素的样品。为了集齐所有元素的样品,他们会购买一些样品,然后利用核聚变制造出剩下元素的样品。
请求出他们至少需要购买的元素样品的数量。
输入输出格式
输入格式:
第一行,(3) 个整数 (n,m,q (1le n,mle 2 imes 10^5, 0le qlemin {n imes m, 2 imes 10^5}))。
之后的 (q) 行,每行 (2) 个整数 (r_i, c_i (1le r_ile n,1le c_ile m))。保证给定的元素互不相同。
输出格式:
输出一个整数,表示至少需要购买的元素样品的数量。
输入输出样例
输入样例#1:
2 2 3 1 2 2 2 2 1输出样例#1:
0输入样例#2:
1 5 3 1 3 1 1 1 5输出样例#2:
2输入样例#3:
4 3 6 1 2 1 3 2 2 2 3 3 1 3 3输出样例#3:
1样例解释
说明
每个样例解释中有两个矩阵。
第一个表示初始状况(其中,打叉的是原本就有样品的元素)。
第二个表示最终集齐样品时的状况(其中,蓝圈代表核聚变得到的样品,蓝圈中的数字表示得到样品的顺序,红圈表示购买的样品)。样例解释 1
通过给定的三种元素,可以得到第四种元素的样品。
样例解释 2
由于给定的元素只有一行,无法使用核聚变,只能购买剩余的两种元素的样品。
样例解释 3
集齐所有元素的方法不唯一,以下是一种方法。其中,元素 ((4,2)) 只有在购买元素 ((4,1)) 的样品,和反应得到元素 ((1,1)) 的样品后才能得到。
子任务
注意:当且仅当你通过了一个子任务下的所有测试点,你将获得此子任务的分数。
子任务编号 分数 (n) (m) (q) (1) (10) (n=2) (m=2) (0le qle 4) (2) (17) (1 le n le 2) (1 le m le 20) (0 le q le 20) (3) (8) (1 le n le 20) (1 le m le 20) (q=0) (4) (20) (1 le n le 20) (1 le m le 20) (0le q le 400) (5) (30) (1 le n le 1 imes 10^4) (1 le m le 1 imes 10^4) (1 le q le 1 imes 10^5) (6) (15) (1 le n le 2 imes 10^5) (1 le m le 2 imes 10^5) (1 le q le 2 imes 10^5)
题解:
一开始总在找规律,比如先放没放过的行或列,先把给出的元素全部聚变一遍……
实际上在这个网格图中,我们把每行、每列均抽象为一个点,可以看成是一个二分图,每个点连接了它的行和列。
那么当一对行、列连通而它们之间又没有直接连边时,可以通过它的路径生成同时在这一行且在这一列的那个点。因此不需要直接连边。
那么我们计算把整个二分图连通需要多少条边,就是连通块个数-1。
Code:
#include<cstdio>
#include<cstring>
struct edge
{
int n,nxt;
edge(int n,int nxt)
{
this->n=n;
this->nxt=nxt;
}
edge(){}
}e[400100];
int head[400100],ecnt=-1;
void add(int from,int to)
{
e[++ecnt]=edge(to,head[from]);
head[from]=ecnt;
e[++ecnt]=edge(from,head[to]);
head[to]=ecnt;
}
bool used[400100];
int dfs(int x)
{
used[x]=1;
for(int i=head[x];~i;i=e[i].nxt)
if(!used[e[i].n])
dfs(e[i].n);
return 1;
}
int main()
{
memset(head,-1,sizeof(head));
int n,m,k,u,v;
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=k;++i)
{
scanf("%d%d",&u,&v);
add(u,n+v);
}
int ans=0;
for(int i=1;i<=n+m;++i)
if(!used[i])
ans+=dfs(i);
printf("%d
",ans-1);
return 0;
}