学习链接:http://blog.csdn.net/lwt36/article/details/48908031
学习扫描线主要学习的是一种扫描的思想,后期可以求解很多问题。
扫描线求矩形周长并
hdu 1928
Picture
Time Limit: 6000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 4795 Accepted Submission(s): 2339
Problem Description
A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.
Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.

The corresponding boundary is the whole set of line segments drawn in Figure 2.
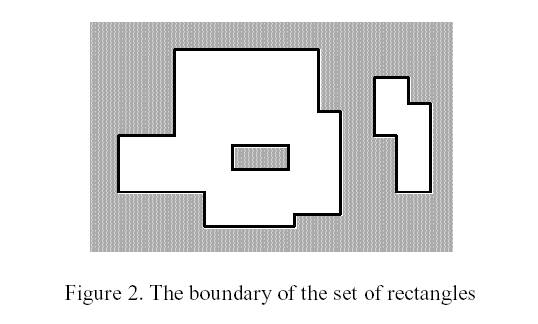
The vertices of all rectangles have integer coordinates.
Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.

The corresponding boundary is the whole set of line segments drawn in Figure 2.

The vertices of all rectangles have integer coordinates.
Input
Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.
0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.
Please process to the end of file.
0 <= number of rectangles < 5000
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.
Please process to the end of file.
Output
Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.
Sample Input
7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16
Sample Output
228
Source
Recommend
linle
1 //#pragma comment(linker, "/STACK:1024000000,1024000000") 2 #include<cstdio> 3 #include<iostream> 4 #include<cstring> 5 #include<algorithm> 6 #include<cmath> 7 #define clr(x) memset(x,0,sizeof(x)) 8 #define MAXN 50010 9 using namespace std; 10 struct edgx 11 { 12 int l,u,x; 13 int d; 14 }edgex[MAXN]; 15 struct edgy 16 { 17 int l,r,y; 18 int d; 19 }edgey[MAXN]; 20 struct seg 21 { 22 int l,r,cov,len; 23 }segt[MAXN<<2]; 24 int cntx,cnty; 25 int x[MAXN],y[MAXN],vec[MAXN]; 26 bool cmpy(edgy a,edgy b) 27 { 28 if(a.y==b.y) return a.d>b.d; 29 return a.y<b.y; 30 } 31 bool cmpx(edgx a,edgx b) 32 { 33 if(a.x==b.x) return a.d>b.d; 34 return a.x<b.x; 35 } 36 void init(int i,int l,int r) 37 { 38 segt[i]=(seg){l,r,0,0}; 39 if(l==r) 40 return ; 41 int mid=(l+r)>>1; 42 init(i<<1,l,mid); 43 init(i<<1|1,mid+1,r); 44 return ; 45 } 46 void pushup(int i) 47 { 48 if(segt[i].cov) 49 { 50 segt[i].len=vec[segt[i].r+1]-vec[segt[i].l]; 51 } 52 else if(segt[i].l==segt[i].r) 53 { 54 segt[i].len=0; 55 } 56 else 57 { 58 segt[i].len=segt[i<<1].len+segt[i<<1|1].len; 59 } 60 return ; 61 } 62 void update(int i,int l,int r,int value) 63 { 64 if(segt[i].l>=l && segt[i].r<=r) 65 { 66 segt[i].cov+=value; 67 pushup(i); 68 return ; 69 } 70 int mid=(segt[i].l+segt[i].r)>>1; 71 if(mid>=r) 72 { 73 update(i<<1,l,r,value); 74 } 75 else if(mid<l) 76 { 77 update(i<<1|1,l,r,value); 78 } 79 else 80 { 81 update(i<<1,l,r,value); 82 update(i<<1|1,l,r,value); 83 } 84 pushup(i); 85 return ; 86 } 87 int main() 88 { 89 int x1,x2,y1,y2,n,m,T,ans,l,r,k; 90 while(scanf("%d",&n)!=EOF) 91 { 92 cntx=0; 93 cnty=0; 94 for(int i=1;i<=n;i++) 95 { 96 scanf("%d%d%d%d",&x1,&y1,&x2,&y2); 97 edgex[++cntx]=(edgx){y1,y2,x1,1}; 98 x[cntx]=x1; 99 edgex[++cntx]=(edgx){y1,y2,x2,-1}; 100 x[cntx]=x2; 101 edgey[++cnty]=(edgy){x1,x2,y1,1}; 102 y[cnty]=y1; 103 edgey[++cnty]=(edgy){x1,x2,y2,-1}; 104 y[cnty]=y2; 105 } 106 n<<=1; 107 ans=0; 108 memcpy(vec,x,sizeof(x)); 109 sort(vec+1,vec+n+1); 110 m=unique(vec+1,vec+n+1)-vec-1; 111 sort(edgey+1,edgey+n+1,cmpy); 112 init(1,1,m); 113 for(int i=1;i<=n;i++) 114 if(edgey[i].l<edgey[i].r) 115 { 116 k=segt[1].len; 117 l=lower_bound(vec+1,vec+m+1,edgey[i].l)-vec; 118 r=lower_bound(vec+1,vec+m+1,edgey[i].r)-vec; 119 update(1,l,r-1,edgey[i].d); 120 ans+=abs(segt[1].len-k); 121 } 122 memcpy(vec,y,sizeof(y)); 123 sort(vec+1,vec+n+1); 124 m=unique(vec+1,vec+n+1)-vec-1; 125 sort(edgex+1,edgex+n+1,cmpx); 126 init(1,1,m); 127 for(int i=1;i<=n;i++) 128 if(edgex[i].l<edgex[i].u) 129 { 130 k=segt[1].len; 131 l=lower_bound(vec+1,vec+m+1,edgex[i].l)-vec; 132 r=lower_bound(vec+1,vec+m+1,edgex[i].u)-vec; 133 update(1,l,r-1,edgex[i].d); 134 ans+=abs(segt[1].len-k); 135 } 136 printf("%d ",ans); 137 } 138 return 0; 139 }
hdu 1255 矩阵面积交
覆盖的面积
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 5718 Accepted Submission(s): 2854
Problem Description
给定平面上若干矩形,求出被这些矩形覆盖过至少两次的区域的面积.


Input
输入数据的第一行是一个正整数T(1<=T<=100),代表测试数据的数量.每个测试数据的第一行是一个正整数N(1<=N<=1000),代表矩形的数量,然后是N行数据,每一行包含四个浮点数,代表平面上的一个矩形的左上角坐标和右下角坐标,矩形的上下边和X轴平行,左右边和Y轴平行.坐标的范围从0到100000.
注意:本题的输入数据较多,推荐使用scanf读入数据.
注意:本题的输入数据较多,推荐使用scanf读入数据.
Output
对于每组测试数据,请计算出被这些矩形覆盖过至少两次的区域的面积.结果保留两位小数.
Sample Input
2
5
1 1 4 2
1 3 3 7
2 1.5 5 4.5
3.5 1.25 7.5 4
6 3 10 7
3
0 0 1 1
1 0 2 1
2 0 3 1
Sample Output
7.63
0.00
Author
Ignatius.L & weigang Lee
1 //#pragma comment(linker, "/STACK:1024000000,1024000000") 2 #include<cstdio> 3 #include<iostream> 4 #include<cstring> 5 #include<algorithm> 6 #include<cmath> 7 #define clr(x) memset(x,0,sizeof(x)) 8 #define MAXN 10010 9 using namespace std; 10 struct edg 11 { 12 double l,r,y; 13 int d; 14 }edge[MAXN]; 15 struct seg 16 { 17 int l,r,cov; 18 double len1,len2; 19 }segt[MAXN<<2]; 20 int cnt; 21 double x[MAXN]; 22 bool cmp(edg a,edg b) 23 { 24 if(a.y==b.y) return a.d>b.d; 25 return a.y<b.y; 26 } 27 double max(double a,double b) 28 { 29 return a>b?a:b; 30 } 31 void init(int i,int l,int r) 32 { 33 segt[i]=(seg){l,r,0,0,0}; 34 if(l==r) 35 return ; 36 int mid=(l+r)>>1; 37 init(i<<1,l,mid); 38 init(i<<1|1,mid+1,r); 39 return ; 40 } 41 void pushup(int i) 42 { 43 if(segt[i].cov>=2) 44 { 45 segt[i].len2=segt[i].len1=x[segt[i].r+1]-x[segt[i].l]; 46 } 47 else if(segt[i].cov==1) 48 { 49 segt[i].len1=x[segt[i].r+1]-x[segt[i].l]; 50 if(segt[i].l==segt[i].r) 51 segt[i].len2=0; 52 else 53 segt[i].len2=max(segt[i<<1].len1,segt[i<<1].len2)+max(segt[i<<1|1].len1,segt[i<<1|1].len2); 54 } 55 else 56 { 57 if(segt[i].l==segt[i].r) 58 { 59 segt[i].len1=segt[i].len2=0; 60 } 61 else 62 { 63 segt[i].len2=segt[i<<1].len2+segt[i<<1|1].len2; 64 segt[i].len1=segt[i<<1].len1+segt[i<<1|1].len1; 65 } 66 } 67 return ; 68 } 69 void update(int i,int l,int r,int value) 70 { 71 if(segt[i].l>=l && segt[i].r<=r) 72 { 73 segt[i].cov+=value; 74 pushup(i); 75 return ; 76 } 77 int mid=(segt[i].l+segt[i].r)>>1; 78 if(mid>=r) 79 { 80 update(i<<1,l,r,value); 81 } 82 else if(mid<l) 83 { 84 update(i<<1|1,l,r,value); 85 } 86 else 87 { 88 update(i<<1,l,r,value); 89 update(i<<1|1,l,r,value); 90 } 91 pushup(i); 92 return ; 93 } 94 int main() 95 { 96 int T,n,m,k,u,v; 97 double x1,x2,y1,y2,ans,l,r; 98 scanf("%d",&T); 99 while(T--) 100 { 101 scanf("%d",&n); 102 cnt=0; 103 ans=0; 104 for(int i=1;i<=n;i++) 105 { 106 scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2); 107 edge[++cnt]=(edg){x1,x2,y1,1}; 108 x[cnt]=x1; 109 edge[++cnt]=(edg){x1,x2,y2,-1}; 110 x[cnt]=x2; 111 } 112 n<<=1; 113 sort(x+1,x+n+1); 114 m=unique(x+1,x+n+1)-x-1; 115 sort(edge+1,edge+n+1,cmp); 116 init(1,1,m); 117 for(int i=1;i<n;i++) 118 if(edge[i].r>edge[i].l) 119 { 120 l=lower_bound(x+1,x+m+1,edge[i].l)-x; 121 r=lower_bound(x+1,x+m+1,edge[i].r)-x; 122 update(1,l,r-1,edge[i].d); 123 ans+=segt[1].len2*(edge[i+1].y-edge[i].y); 124 } 125 printf("%0.2lf ",ans); 126 } 127 return 0; 128 }
hdu 1542 [POJ 1151] 区间面积并
Atlantis
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 12537 Accepted Submission(s): 5257
Problem Description
There are several ancient Greek texts that contain descriptions of the fabled island Atlantis. Some of these texts even include maps of parts of the island. But unfortunately, these maps describe different regions of Atlantis. Your friend Bill has to know the total area for which maps exist. You (unwisely) volunteered to write a program that calculates this quantity.
Input
The input file consists of several test cases. Each test case starts with a line containing a single integer n (1<=n<=100) of available maps. The n following lines describe one map each. Each of these lines contains four numbers x1;y1;x2;y2 (0<=x1<x2<=100000;0<=y1<y2<=100000), not necessarily integers. The values (x1; y1) and (x2;y2) are the coordinates of the top-left resp. bottom-right corner of the mapped area.
The input file is terminated by a line containing a single 0. Don’t process it.
The input file is terminated by a line containing a single 0. Don’t process it.
Output
For each test case, your program should output one section. The first line of each section must be “Test case #k”, where k is the number of the test case (starting with 1). The second one must be “Total explored area: a”, where a is the total explored area (i.e. the area of the union of all rectangles in this test case), printed exact to two digits to the right of the decimal point.
Output a blank line after each test case.
Output a blank line after each test case.
Sample Input
2
10 10 20 20
15 15 25 25.5
0
Sample Output
Test case #1
Total explored area: 180.00
Source
卡格式,不说了,都是泪。
1 //#pragma comment(linker, "/STACK:1024000000,1024000000") 2 #include<cstdio> 3 #include<iostream> 4 #include<cstring> 5 #include<algorithm> 6 #include<cmath> 7 #define clr(x) memset(x,0,sizeof(x)) 8 #define MAXN 10010 9 using namespace std; 10 struct edg 11 { 12 double l,r,y; 13 int d; 14 }edge[MAXN]; 15 struct seg 16 { 17 int l,r,cov; 18 double len; 19 }segt[MAXN<<2]; 20 int cnt; 21 double x[MAXN]; 22 bool cmp(edg a,edg b) 23 { 24 if(a.y==b.y) return a.d>b.d; 25 return a.y<b.y; 26 } 27 double max(double a,double b) 28 { 29 return a>b?a:b; 30 } 31 void init(int i,int l,int r) 32 { 33 segt[i]=(seg){l,r,0,0}; 34 if(l==r) 35 return ; 36 int mid=(l+r)>>1; 37 init(i<<1,l,mid); 38 init(i<<1|1,mid+1,r); 39 return ; 40 } 41 void pushup(int i) 42 { 43 if(segt[i].cov) 44 { 45 segt[i].len=x[segt[i].r+1]-x[segt[i].l]; 46 } 47 else if(segt[i].l==segt[i].r) 48 { 49 segt[i].len=0; 50 } 51 else 52 { 53 segt[i].len=segt[i<<1].len+segt[i<<1|1].len; 54 } 55 return ; 56 } 57 void update(int i,int l,int r,int value) 58 { 59 if(segt[i].l>=l && segt[i].r<=r) 60 { 61 segt[i].cov+=value; 62 pushup(i); 63 return ; 64 } 65 int mid=(segt[i].l+segt[i].r)>>1; 66 if(mid>=r) 67 { 68 update(i<<1,l,r,value); 69 } 70 else if(mid<l) 71 { 72 update(i<<1|1,l,r,value); 73 } 74 else 75 { 76 update(i<<1,l,r,value); 77 update(i<<1|1,l,r,value); 78 } 79 pushup(i); 80 return ; 81 } 82 int main() 83 { 84 int T,n,m,k,u,v; 85 double x1,x2,y1,y2,ans,l,r; 86 int kase=0; 87 while(scanf("%d",&n) && n!=0) 88 { 89 printf("Test case #%d ",++kase); 90 cnt=0; 91 ans=0; 92 for(int i=1;i<=n;i++) 93 { 94 scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2); 95 edge[++cnt]=(edg){x1,x2,y1,1}; 96 x[cnt]=x1; 97 edge[++cnt]=(edg){x1,x2,y2,-1}; 98 x[cnt]=x2; 99 } 100 n<<=1; 101 sort(x+1,x+n+1); 102 m=unique(x+1,x+n+1)-x-1; 103 sort(edge+1,edge+n+1,cmp); 104 init(1,1,m); 105 for(int i=1;i<n;i++) 106 if(edge[i].r>edge[i].l) 107 { 108 l=lower_bound(x+1,x+m+1,edge[i].l)-x; 109 r=lower_bound(x+1,x+m+1,edge[i].r)-x; 110 update(1,l,r-1,edge[i].d); 111 ans+=segt[1].len*(edge[i+1].y-edge[i].y); 112 } 113 printf("Total explored area: %0.2lf ",ans); 114 printf(" "); 115 } 116 return 0; 117 }