修仙场,没脑子,C边界判错一直在写mdzz。。D根本没怎么想。
第二天起来想了想D这不是水题吗立马A了。看了看E一开始想分配问题后来发觉想岔了,只需要每次都把树最后分配的点移到最前面就好了。
To make a paper airplane, one has to use a rectangular piece of paper. From a sheet of standard size you can make ss airplanes.
A group of kk people decided to make nn airplanes each. They are going to buy several packs of paper, each of them containing pp sheets, and then distribute the sheets between the people. Each person should have enough sheets to make nn airplanes. How many packs should they buy?
The only line contains four integers kk, nn, ss, pp (1≤k,n,s,p≤1041≤k,n,s,p≤104) — the number of people, the number of airplanes each should make, the number of airplanes that can be made using one sheet and the number of sheets in one pack, respectively.
Print a single integer — the minimum number of packs they should buy.
5 3 2 3
4
5 3 100 1
5
In the first sample they have to buy 44 packs of paper: there will be 1212 sheets in total, and giving 22 sheets to each person is enough to suit everyone's needs.
In the second sample they have to buy a pack for each person as they can't share sheets.
水题,推个小公式就好了。


1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 using namespace std; 4 int n,k,s,p; 5 int main() 6 { 7 scanf("%d%d%d%d",&k,&n,&s,&p); 8 printf("%d ",(((n-1)/s+1)*k-1)/p+1); 9 return 0; 10 }
Arkady is playing Battleship. The rules of this game aren't really important.
There is a field of n×nn×n cells. There should be exactly one kk-decker on the field, i. e. a ship that is kk cells long oriented either horizontally or vertically. However, Arkady doesn't know where it is located. For each cell Arkady knows if it is definitely empty or can contain a part of the ship.
Consider all possible locations of the ship. Find such a cell that belongs to the maximum possible number of different locations of the ship.
The first line contains two integers nn and kk (1≤k≤n≤1001≤k≤n≤100) — the size of the field and the size of the ship.
The next nn lines contain the field. Each line contains nn characters, each of which is either '#' (denotes a definitely empty cell) or '.' (denotes a cell that can belong to the ship).
Output two integers — the row and the column of a cell that belongs to the maximum possible number of different locations of the ship.
If there are multiple answers, output any of them. In particular, if no ship can be placed on the field, you can output any cell.
4 3
#..#
#.#.
....
.###
3 2
10 4
#....##...
.#...#....
..#..#..#.
...#.#....
.#..##.#..
.....#...#
...#.##...
.#...#.#..
.....#..#.
...#.#...#
6 1
19 6
##..............###
#......#####.....##
.....#########.....
....###########....
...#############...
..###############..
.#################.
.#################.
.#################.
.#################.
#####....##....####
####............###
####............###
#####...####...####
.#####..####..#####
...###........###..
....###########....
.........##........
#.................#
1 8
The picture below shows the three possible locations of the ship that contain the cell (3,2)(3,2) in the first sample.
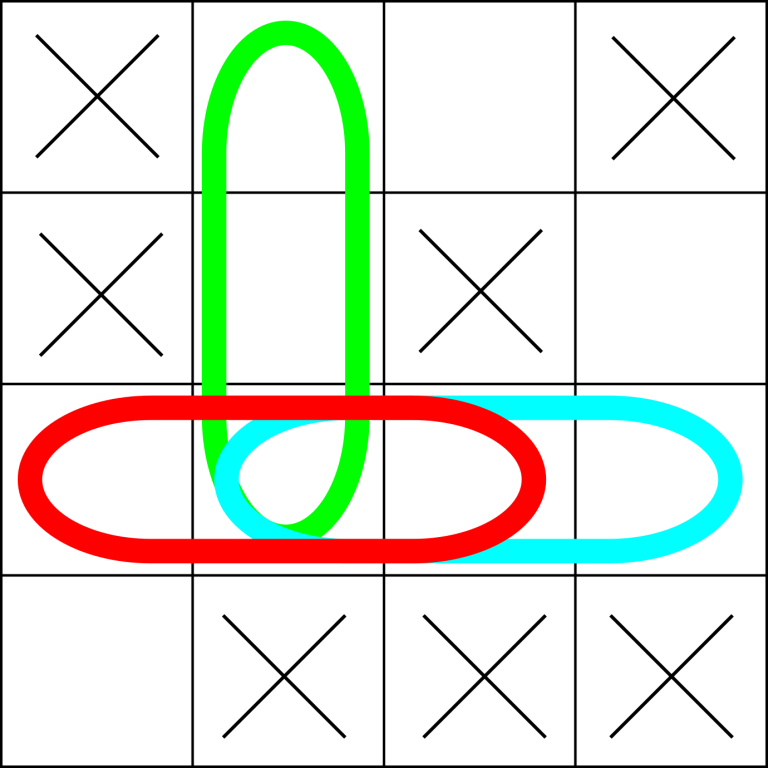
然后这题的话,就是统计下每个点向上、向下、向左、向右最长能达到的船体长度,然后最后算算每个点竖着(上下)这一维能有一部分是他的情况下有多少船,横着有多少船。由于包含自己,所以向上下左右最多延展k长度。因此超过k的算为k然后做个加减法就能算出包含这个点的船只数量。在每个点取最大点就是答案案。


1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define mod 1000000007 5 #define LL long long 6 #define INF 0x3f3f3f3f 7 using namespace std; 8 const int N=1e2+10; 9 int a[N][N],up[N][N],lt[N][N],rt[N][N],down[N][N]; 10 char s[N]; 11 int n,m,k,t,sized,x,y,ans,p; 12 int main() 13 { 14 scanf("%d%d",&n,&sized); 15 for(int i=1;i<=n;i++) 16 { 17 scanf("%s",s); 18 for(int j=0;j<n;j++) 19 if(s[j]=='.') 20 a[i][j+1]=1; 21 } 22 for(int i=1;i<=n;i++) 23 for(int j=1;j<=n;j++) 24 if(a[i][j]) 25 { 26 lt[i][j]=lt[i][j-1]+1; 27 up[i][j]=up[i-1][j]+1; 28 } 29 30 for(int i=n;i>=1;i--) 31 for(int j=n;j>=1;j--) 32 if(a[i][j]) 33 { 34 rt[i][j]=rt[i][j+1]+1; 35 down[i][j]=down[i+1][j]+1; 36 } 37 ans=0; 38 x=y=1; 39 for(int i=1;i<=n;i++) 40 for(int j=1;j<=n;j++) 41 if(a[i][j]) 42 { 43 p=0; 44 if(min(lt[i][j],sized)+min(rt[i][j],sized)>sized) 45 p+=min(lt[i][j],sized)+min(rt[i][j],sized)-sized; 46 if(min(up[i][j],sized)+min(down[i][j],sized)>sized) 47 p+=min(up[i][j],sized)+min(down[i][j],sized)-sized; 48 if(p>ans) 49 { 50 ans=p; 51 x=i; 52 y=j; 53 } 54 } 55 printf("%d %d ",x,y); 56 return 0; 57 }
kk people want to split nn candies between them. Each candy should be given to exactly one of them or be thrown away.
The people are numbered from 11 to kk, and Arkady is the first of them. To split the candies, Arkady will choose an integer xx and then give the first xx candies to himself, the next xx candies to the second person, the next xx candies to the third person and so on in a cycle. The leftover (the remainder that is not divisible by xx) will be thrown away.
Arkady can't choose xx greater than MM as it is considered greedy. Also, he can't choose such a small xx that some person will receive candies more than DD times, as it is considered a slow splitting.
Please find what is the maximum number of candies Arkady can receive by choosing some valid xx.
The only line contains four integers nn, kk, MM and DD (2≤n≤10182≤n≤1018, 2≤k≤n2≤k≤n, 1≤M≤n1≤M≤n, 1≤D≤min(n,1000)1≤D≤min(n,1000), M⋅D⋅k≥nM⋅D⋅k≥n) — the number of candies, the number of people, the maximum number of candies given to a person at once, the maximum number of times a person can receive candies.
Print a single integer — the maximum possible number of candies Arkady can give to himself.
Note that it is always possible to choose some valid xx.
20 4 5 2
8
30 9 4 1
4
In the first example Arkady should choose x=4x=4. He will give 44 candies to himself, 44 candies to the second person, 44 candies to the third person, then 44 candies to the fourth person and then again 44 candies to himself. No person is given candies more than 22 times, and Arkady receives 88 candies in total.
Note that if Arkady chooses x=5x=5, he will receive only 55 candies, and if he chooses x=3x=3, he will receive only 3+3=63+3=6 candies as well as the second person, the third and the fourth persons will receive 33 candies, and 22 candies will be thrown away. He can't choose x=1x=1 nor x=2x=2 because in these cases he will receive candies more than 22 times.
In the second example Arkady has to choose x=4x=4, because any smaller value leads to him receiving candies more than 11 time.
果然二分保平安,由于本傻子错想一个公式确定了x的左边界,而这个公式是错的导致我一直没过题。二分保平安,以后二分确定边界了。。。然后这题的话题目告诉你D≤1000,那你枚举分配轮数就好了。设总共进行了t+1轮,那么第一个人在总共t+1轮分到最多的是什么情况呢?那当然是第t+1轮第一次分给他糖果之后,剩下糖果最少的时候他分到最多。因此我们每一轮最多的x由n/(tk+1)得出。超边界就不计算他。然后答案就在左边界,右边界以及每一轮分到最多的情况中诞生。


1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define mod 1000000007 5 #define LL long long 6 #define INF 0x3f3f3f3f 7 using namespace std; 8 LL n,k,m,d,lt,rt,l,r,p,t,pt; 9 LL ans=INF; 10 LL search(LL n,LL k,LL m,LL d) 11 { 12 LL lt=1,rt=m,p,mid; 13 while(lt!=rt) 14 { 15 mid=(lt+rt)>>1; 16 p=(n-1)/k/mid+1; 17 if(p<=d) 18 rt=mid; 19 else 20 lt=mid+1; 21 } 22 return lt; 23 } 24 int main() 25 { 26 scanf("%I64d%I64d%I64d%I64d",&n,&k,&m,&d); 27 rt=m; 28 lt=search(n,k,m,d); 29 l=n/k/rt; 30 ans=0; 31 ans=max(((n/lt-1)/k+1)*lt,((n/rt-1)/k+1)*rt); 32 for(LL i=l;i<=d;i++) 33 { 34 p=n/(i*k+1); 35 if(p>rt) 36 continue; 37 if(p<lt) 38 break; 39 ans=max(ans,((n/p-1)/k+1)*p); 40 } 41 printf("%I64d ",ans); 42 return 0; 43 44 }
A lot of frogs want to cross a river. A river is ww units width, but frogs can only jump ll units long, where l<wl<w. Frogs can also jump on lengths shorter than ll. but can't jump longer. Hopefully, there are some stones in the river to help them.
The stones are located at integer distances from the banks. There are aiai stones at the distance of ii units from the bank the frogs are currently at. Each stone can only be used once by one frog, after that it drowns in the water.
What is the maximum number of frogs that can cross the river, given that then can only jump on the stones?
The first line contains two integers ww and ll (1≤l<w≤1051≤l<w≤105) — the width of the river and the maximum length of a frog's jump.
The second line contains w−1w−1 integers a1,a2,…,aw−1a1,a2,…,aw−1 (0≤ai≤1040≤ai≤104), where aiai is the number of stones at the distance ii from the bank the frogs are currently at.
Print a single integer — the maximum number of frogs that can cross the river.
10 5
0 0 1 0 2 0 0 1 0
3
10 3
1 1 1 1 2 1 1 1 1
3
In the first sample two frogs can use the different stones at the distance 55, and one frog can use the stones at the distances 33 and then 88.
In the second sample although there are two stones at the distance 55, that does not help. The three paths are: 0→3→6→9→100→3→6→9→10, 0→2→5→8→100→2→5→8→10, 0→1→4→7→100→1→4→7→10.
我的想法是用最小割最大流定理去想(贪)。
不可避免的,如果最多有k只到对岸,选择任意一个位置 $ i $,以位置$i$前面的任意一个位置为源点,一步越过位置$i$的流量总和 $flow[i]≥k$。那这个流量总和 $ flow[i] $ 就是 $ [i-l+1,i] $ 的石头总数 $ sum[i-l+1,i] $。而答案明显就是这些流量总和中最小的那个。因此求个前缀和,然后$O(w) $地遍历一遍找最小的一个 $ sum[i-l+1,i] $ 即为答案。


1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define mod 1000000007 5 #define LL long long 6 #define INF 0x3f3f3f3f 7 using namespace std; 8 const int N=1e5+10; 9 int a[N],pre[N]; 10 int n,l; 11 int ans; 12 int main() 13 { 14 ans=INF; 15 scanf("%d%d",&n,&l); 16 for(int i=1;i<n;i++) 17 scanf("%d",a+i); 18 for(int i=1;i<n;i++) 19 pre[i]=pre[i-1]+a[i]; 20 for(int i=l;i<n;i++) 21 ans=min(pre[i]-pre[i-l],ans); 22 printf("%d ",ans); 23 return 0; 24 }
Arkady's code contains nn variables. Each variable has a unique name consisting of lowercase English letters only. One day Arkady decided to shorten his code.
He wants to replace each variable name with its non-empty prefix so that these new names are still unique (however, a new name of some variable can coincide with some old name of another or same variable). Among such possibilities he wants to find the way with the smallest possible total length of the new names.
A string aa is a prefix of a string bb if you can delete some (possibly none) characters from the end of bb and obtain aa.
Please find this minimum possible total length of new names.
The first line contains a single integer nn (1≤n≤1051≤n≤105) — the number of variables.
The next nn lines contain variable names, one per line. Each name is non-empty and contains only lowercase English letters. The total length of these strings is not greater than 105105. The variable names are distinct.
Print a single integer — the minimum possible total length of new variable names.
3
codeforces
codehorses
code
6
5
abba
abb
ab
aa
aacada
11
3
telegram
digital
resistance
3
In the first example one of the best options is to shorten the names in the given order as "cod", "co", "c".
In the second example we can shorten the last name to "aac" and the first name to "a" without changing the other names.
那最后一题则是一个想法题。
先写个trie,那么每个字符串对应trie一个节点,并且我们标记这样的节点。那么我们的任务是通过上移标记让这些标记节点深度总和最小。我们dfs一下。假如在节点u,我们先处理出u子树所有节点标记的深度。如果u没有被标记,那么我们把最深的一个节点的标记上移到u节点。这样不断贪心得出的答案是最优的。那么我们对每个点写一个优先队列来维护标记节点的深度,移动标记就相当于把优先队列深度最高的出队,然后把该节点u的深度入队。


1 #include<bits/stdc++.h> 2 #define clr(x) memset(x,0,sizeof(x)) 3 #define clr_1(x) memset(x,-1,sizeof(x)) 4 #define mod 1000000007 5 #define LL long long 6 #define INF 0x3f3f3f3f 7 #define pb(x) push_back(x) 8 using namespace std; 9 const int N=1e5+10; 10 const int type=26; 11 char s[N]; 12 int n,m,k; 13 struct node 14 { 15 int next[type],num; 16 }trie[N]; 17 priority_queue<int> slen[N]; 18 int ans,ct,tot; 19 int makenode() 20 { 21 tot++; 22 memset(&trie[tot],0,sizeof(trie[tot])); 23 return tot; 24 } 25 void init() 26 { 27 tot=-1; 28 makenode(); 29 ans=0; 30 return ; 31 } 32 void add(char *s) 33 { 34 int now=0,p; 35 int len=strlen(s); 36 for(int i=0;s[i];i++) 37 { 38 p=s[i]-'a'; 39 if(!trie[now].next[p]) 40 trie[now].next[p]=makenode(); 41 now=trie[now].next[p]; 42 } 43 trie[now].num++; 44 return ; 45 } 46 void dfs(int now,int dep) 47 { 48 int p; 49 for(int i=0;i<type;i++) 50 { 51 p=trie[now].next[i]; 52 if(p) 53 { 54 dfs(p,dep+1); 55 if(slen[p].size()>slen[now].size()) slen[p].swap(slen[now]); 56 while(!slen[p].empty()) 57 { 58 slen[now].push(slen[p].top()); 59 slen[p].pop(); 60 } 61 } 62 } 63 if(trie[now].num==0) 64 { 65 slen[now].pop(); 66 slen[now].push(dep); 67 } 68 else 69 slen[now].push(dep); 70 return ; 71 } 72 int main() 73 { 74 scanf("%d",&n); 75 init(); 76 for(int i=1;i<=n;i++) 77 { 78 scanf("%s",s); 79 add(s); 80 } 81 for(int i=0;i<type;i++) 82 if(trie[0].next[i]) 83 { 84 k=trie[0].next[i]; 85 dfs(k,1); 86 while(!slen[k].empty()) 87 { 88 ans+=slen[k].top(); 89 slen[k].pop(); 90 } 91 } 92 printf("%d ",ans); 93 return 0; 94 }