算法训练 Bus Tour

问题描述

　　想象你是一个在Warsaw的游客，而且预订了一次乘车旅行，去城镇外看一些令人惊异的景点。这辆公共汽车首先围绕城镇行驶一段时间（一段很长的时间，由于Warsaw是一个大城市），把在各自旅馆的人们带上。接着它就去了那个令人惊异的景点，几个小时后又回到城市中，再一次行驶到每一个旅馆，这一次把乘客放下。
　　由于某种原因，每当你这样做的时候，你的旅馆总是第一个要上车的，而且是最后一个才下车的，意味着你不得不忍受两段经过所有当地旅馆的不那么愉快的旅行。这很明显不是你想要做的事（除非由于某种原因你真的要进入那些旅馆），所以让我们来做个改变。我们将开发一些软件使得那些观光公司能够把它们的乘车旅行路线安排得更公平——尽管这有时候可能会导致每一个人的总距离更长，但公平就是公平，不是吗？
　　对于这个问题，有一个起始位置（观光公司的总部），h个需要接送游客的旅馆和一个目的地位置（令人惊异的景点）。我们需要找到一条路径，从总部出发，经过所有的旅馆，到景点去，再回来再一次经过所有的旅馆（可能按照不同的顺序），最后返回总部。为了保证没有一个游客（特别是你）被迫忍受两个完整的旅馆旅行，我们要求在去景点的路上接游客的前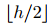个旅馆，在回来的路上也得是前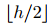个让游客下车的。受制于这些限制条件，我们想让整个公车旅行尽可能短。注意这些限制条件可能会迫使公共汽车经过某个旅馆但是不停下来（这不算做让游客下车），后来再来这里让游客下车，样例就说明了这种情况。

输入格式

　　第一行包含两个整数n和m满足3≤n≤20,2≤m，n是位置的总数（旅馆，总部和景点），m是汽车能在两个位置之间行驶的路径条数。
　　n个不同的位置被标号为0到n-1,0是总部，1到n-2是旅馆，而n-1是景点。假定任意一对位置之间最多只有一条直接路径，而且从任意一个位置都能到达任意另一个位置（并不一定直接到达）。
　　接下来m行，每行包含三个整数u，v和t，满足0≤u，v≤n-1，u≠v，1≤t≤3600，表示公共汽车可以在t秒的时间内直接在u和v之间到达（两个方向都可以）。

输出格式

　　一个整数，表示可能的最短路线的总耗时。

样例输入

5 4
0 1 10
1 2 20
2 3 30
3 4 40

样例输出

300

数据规模和约定

　　对于20%的数据：n=3
　　对于50%的数据：3≤n≤10
　　对于100%的数据：3≤n≤20，2≤m

好久不刷题了，帮朋友做的，状压DP+最短路，算了一下复杂度超了。再想起来在写吧。

思路：先floyd处理出来两点之间的最短路 O(n^3) ，然后状压dp[v | (1 << j)][j] = min (dp[v | (1 << j)][j], dp[v][i] + dis[i][j])，枚举状态和两个点。复杂度O(n*n*(1 << (n + 1)) 算了一下虽然10S，但是有点超。

/*************************************************************************
    > File Name: ALGO-176.cpp
    > Author: LyuCheng
    > Created Time: 2018-02-07 00:10
    > Description: 问题可拆分成：
        先处理出来从0访问前h / 2个点 以第i个点为结尾的最短路，然后在枚举
        n - 2个点作为起点，访问后h / 2以 n - 1作为终点的最短路，然后这就
        是去景点的最短路，然后同理求从景点到起点的最短路
        状态转移方程：dp[v | (1 << j)][j] = min (dp[v | (1 << j)][j], dp[v][i] + dis[i][j])
 ************************************************************************/

#include <iostream>
#include <string>
#include <vector>
#include <string.h>

#define MAXN 21
#define INF 0x3f3f3f3f

using namespace std;

int n, m;
int u,v,w;
int mapn[MAXN][MAXN];
int dis[MAXN][MAXN];
int dp[(1 << MAXN)][MAXN]; //dp[i][j] 表示I状态（访问城市的状态）下最后访问j点的最短路的权值
int fdis[MAXN];//经过前h / 2个点的最短路
int edis[MAXN];//经过剩余点的最短路
vector <int> fir;
vector <int> sec;
int fres;
int sres;

void floyd() {
    memcpy(dis, mapn, sizeof mapn);
    for (int i = 0; i < n; ++ i) {
        for (int j = 0; j < n; ++ j) {
            for (int k = 0; k < n; ++ k) {
                dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
            }
        }
    }
}

void addedge(int u, int v, int w) {
    if (mapn[u][v] > w) {
        mapn[u][v] = w;
        mapn[v][u] = w;
    }
}

void frist_half(int s) { //访问前 h / 2 点的最短路
    memset(dp, INF, sizeof dp);
    dp[1][s] = 0;
    for (int v = 0; v < (1 << (n + 1)); ++ v) {
        for (int i = 0; i < n; ++ i) {
            for (int j = 0; j < n; ++ j) {
                    dp[v | (1 << j)][j] = min (dp[v | (1 << j)][j], dp[v][i] + dis[i][j]);
            }
        }
    }    
}

int end_half(int s, int t) { //访问剩余的点的最短路
    memset(dp, INF, sizeof dp);
    dp[1][s] = 0;
    for (int v = 0; v < (1 << (n + 1)); ++ v) {
        for (int i = 0; i < n; ++ i) {
            for (int j = 0; j < n; ++ j) {
                    dp[v | (1 << j)][j] = min (dp[v | (1 << j)][j], dp[v][i] + dis[i][j]);
            }
        }
    }
    int ans = INF;
    for (int i = 0; i < (int) sec.size(); ++ i) {
        ans = min (ans, dp[sec[i]][t]);
    }
    return ans;
}

void init() {
    fres = INF;
    sres = INF;
    memset(mapn, 0, sizeof mapn);
    for (int i = 0; i < MAXN; ++ i) 
        for (int j = 0; j < MAXN; ++ j) 
            mapn[i][j] = (i == j) ? 0 : INF;
    fir.clear();
    sec.clear();
    for (int i = 0; i < (1 << (n + 1)); ++ i) {
        int s = 1;
        for (int j = 1; j < n / 2; ++ j) 
            if ((i & (1 << j)) == 0)
                s = 0;
        if (s == 1)
            fir.push_back(i);
        s = 1;
        for (int j = n / 2; j < n - 1; ++ j)
            if ((i & (1 << j)) == 0)
                s = 0;
        if (s == 1)
            sec.push_back(i);
    }
}

int main() {
//    freopen ("in.txt", "r", stdin);
    scanf ("%d %d", &n, &m);
    init();
    for (int i = 0; i < m; ++ i) {
        scanf ("%d %d %d", &u, &v, &w);
        addedge(u, v, w);
    }
    floyd(); // floyd处理出来两点间的最短路    

    frist_half(0);
    memset(fdis, INF, sizeof fdis);
    for (int i = 0; i < n; ++ i)
        for (int j = 0; j < (int) fir.size(); ++ j) 
            fdis[i] = min (fdis[i], dp[fir[j]][i]);    
    for (int i = 0; i < n; ++ i) 
        fres = min(fres, fdis[i] + end_half(i, n - 1));

    /*----------------------前半段处理完毕------------------------*/

    frist_half(n - 1);
    memset(edis, INF, sizeof edis);
    for (int i = 0; i < n; ++ i)
        for (int j = 0; j < (int) fir.size(); ++ j)
            edis[i] = min (edis[i], dp[fir[j]][i]);    
    for (int i = 0; i < n; ++ i) { 
        int res = end_half(i, 0);
        sres  = min(sres, edis[i] + res);
    }

    printf ("%d
", fres + sres);
    return 0;
}