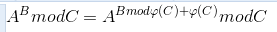Given A,B,C, You should quickly calculate the result of A^B mod C. (1<=A,C<=1000000000,1<=B<=10^1000000).
Input
There are multiply testcases. Each testcase, there is one line contains three integers A, B and C, separated by a single space.
Output
For each testcase, output an integer, denotes the result of A^B mod C.
Sample Input
3 2 4
2 10 1000
Sample Output
1
24
这题的b非常大,只能用字符串处理;
需要一个降幂公式
然后带入欧拉公式,快速幂,快速乘法就可以了
#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<cmath>
#include<string.h>
#include<algorithm>
#define sf scanf
#define pf printf
#define pb push_back
#define mm(a,b) memset((a),(b),sizeof(a))
#include<vector>
typedef __int64 ll;
typedef long double ld;
//const ll mod=1e9+7;
using namespace std;
const double pi=acos(-1.0);
vector<int>v;
char x[1000005];
ll multi(ll a,ll b,ll c)//快速乘
{
ll ans=0;
while(b)
{
if(b&1)
ans=(ans+a)%c;
a=(a+a)%c;
b>>=1;
}
return ans;
}
ll pow(ll a,ll b,ll c)//快速幂
{
ll ans=1,bas=a;
while(b)
{
if(b&1)
ans=multi(ans,bas,c);
bas=multi(bas,bas,c);
b>>=1;
}
return ans;
}
ll p[1000100];
ll ola(ll n){ //欧拉函数
ll i, j, r, aa;
r = n;
aa = n;
mm(p,0);
for(i=2; i<=sqrt(n); i++)
{
if(aa%i==0)
{
r = r/i*(i-1);
while(aa%i==0)
aa /= i;
}
}
if(aa>1)
r = r/aa*(aa-1);
return r;
}
int main()
{
ll a,b,mod;
while(~sf("%I64d %s %I64d",&a,&x,&mod))
{
ll cas=ola(mod);
ll ans=0;
int num=strlen(x);
for(int i=0;i<num;i++)//求那个b%phi(c)
{
ans=ans*10+x[i]-48;
ans%=cas;
}
if(ans<0) ans+=mod;
pf("%I64d
",pow(a,ans+cas,mod));
}
}