一、快速排序扫描分区法
通过单向扫描,双向扫描,以及三指针分区法分别实现快速排序算法。着重理解分区的思想。
单向扫描分区法
思路:用两个指针将数组划分为三个区间,扫描指针(scan_pos)左边是确认小于等于主元的,扫描指针到某个指针(next_bigger_pos)中间为未知的,因此我们将第二个指针(next_bigger_pos)称为未知区间指针,末指针的右边区间为确认大于主元的元素。主元就是具体的划分数组的元素,主元的选择有讲究,这里选择数组的首元素
代码:
import java.util.Arrays; public class QuickSort { public static void main(String[] args) { int arr[] = new int[10]; for(int i=0;i<10;i++){ arr[i] = (int) ((Math.random()+1)*10); } System.out.println("排序前:"+Arrays.toString(arr)); quickSort(arr, 0, arr.length-1); System.out.println("排序后:"+Arrays.toString(arr)); } public static void quickSort(int[]A,int p,int r){ if (p<r) { int q = partition(A,p,r); // 得到分区返回的一个下标 以此划分数组 quickSort(A, p, q-1); quickSort(A, q+1, r); } } private static int partition(int[] A, int p, int r) { int pivot = A[p]; // 主元 int sp = p + 1; // 扫描指针 int bigger = r; // 右侧指针 while(sp<=bigger){ if (A[sp]<=pivot) { // 扫描元素左移,左指针向右移 sp++; }else { swap(A,sp,bigger); // 扫描元素大于主元,二指针的元素交换,右指针左移 bigger--; } } swap(A,p,bigger); return bigger; } private static void swap(int[] A, int p, int bigger) { int temp = A[p]; A[p] = A[bigger]; A[bigger] = temp; } }
结果:
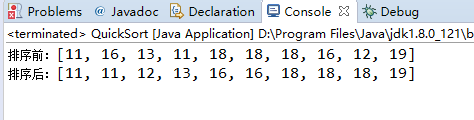
双向扫描分区法
思路:头尾指针往中间扫描,从左找到大于主元的元素,从右找到小于等于主元的元素二者交换,继续扫描,直到左侧无大元素,右侧无小元素。
代码:
import java.util.Arrays; public class QuickSort2 { public static void main(String[] args) { int arr[] = new int[10]; for(int i=0;i<10;i++){ arr[i] = (int) ((Math.random()+1)*10); } System.out.println(Arrays.toString(arr)); quickSort(arr, 0, arr.length-1); System.out.println(Arrays.toString(arr)); } public static void quickSort(int[]A,int p,int r){ if (p<r) { int q = partition2(A,p,r); // 得到分区返回的一个下标 以此划分数组 quickSort(A, p, q-1); quickSort(A, q+1, r); } } //双向扫描分区法 public static int partition2(int[] arr, int p, int r) { int left = p + 1; //左侧扫描指针 int right = r; //右侧指针 int pivot = arr[p]; while(left <= right) { // left不停往右走,直到遇到大于主元的元素 // 循环退出时,left一定是指向第一个大于主元的位置 while(left <= right && arr[left] <= pivot) { left++; } // right不停往左走,直到遇到小于主元的元素 // 循环退出时,right一定是指向从右到左第一个小于于主元的位置 while(left <= right && arr[right] > pivot) { right--; } if(left < right) swap(arr, left, right); } // 循环退出时,两者交错,且right指向的最后一个小于等于主元的位置,也就是主元应该待的位置 swap(arr, p, right); return right; } private static void swap(int[] A, int p, int bigger) { int temp = A[p]; A[p] = A[bigger]; A[bigger] = temp; } }
结果:
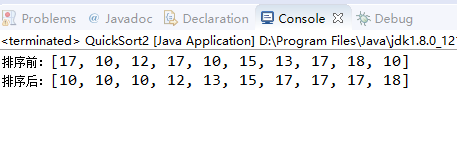
三指针分区法
思路:当待排序数组中,如果有大量相同的元素,则可以三指针分区法,每次将与主元相等的元素找到,排好序,并记录这组与主元相等元素序列的开始下标和结束下标。在进行下次递归排序时,排除这部分相同的元素。从而减少递归次数。
代码:
import java.util.Arrays; public class QuickSort3 { public static void main(String[] args) { int arr[] = new int[10]; for(int i=0;i<10;i++){ arr[i] = (int) ((Math.random()+1)*10); } System.out.println("排序前:"+Arrays.toString(arr)); quickSort(arr, 0, arr.length-1); System.out.println("排序后:"+Arrays.toString(arr)); } public static void quickSort(int[]A,int p,int r){ if (p<r) { int q[] = partition3(A,p,r); // 得到分区返回的一个下标 以此划分数组 quickSort(A, p, q[0]-1); quickSort(A, q[1]+1, r); } } private static int[] partition3(int[] arr, int p, int r) { int s = p + 1; //左扫描指针 int e = s; //记录与主元相等元素序列的开始下标 int bigger = r; //右侧扫描指针 int pivot = arr[p]; //主元 while (s <= bigger) { while(s <= bigger && arr[s] <= pivot) { //当从一开始没有找到与主语相等的元素,且都小于主元时,指针右移 if(s <= bigger && s == e && arr[s] < pivot) { s++; e++; } //如过s!=e时,说明已经找到与主元相等的元素,且e记录的为与主元相等元素的开始下标 //如果下一个元素小于主元,则将小于主元的元素和与主元相等序列的第一个元素交换位置 if(s <= bigger && s != e && arr[s] < pivot) { swap(arr, s, e); e++; s++; } //如果遇到等于主元的元素,左扫描指针++, 记录与主元相等序列的开始下标e不变 if(s <= bigger && arr[s] == pivot) { s++; } } //右侧扫描指针 while(s <= bigger && arr[bigger] > pivot) { bigger--; } //将左侧指针指向大的元素与右侧小于主元的元素交换 if(s <= bigger && arr[s] > arr[bigger]) { swap(arr, s, bigger); } } //最后,数组下标为p的开始元素,和与主元相等序列的前一个元素交换,e-- swap(arr, p, --e); //返回与主元相等序列的开始下标和结束下标 int[] q = {e, bigger}; return q; } private static void swap(int[] A, int p, int bigger) { int temp = A[p]; A[p] = A[bigger]; A[bigger] = temp; } }
结果:

二、快速排序在工程实践中优化方法
1、三点中值法:Arrays.sort()方法就是采用的三点中值法。在上面的例子中,每次取的主元都是待排序子序列的首元素,很大可能不是属于中间的元素,从而容易加大递归的层数。三点中值法就是对待排序数组的开始,中间,最后三个元素的大小进行比较,然后取中间值,这样很大概率能使主元成为中间的元素,从而减少递归层数。
1 //三点中值法 2 public static int partition(int[] arr, int p, int r) { 3 //优化,在p, r, mid之间,选一个中间值作为主元 4 int midIndex = p + ((r - p) >> 1);//中间下标 5 int midValueIndex = -1;//中值的下标 6 if(arr[p] <= arr[midIndex] && arr[p] >= arr[r]) { 7 midValueIndex = p; 8 }else if(arr[r] <= arr[midIndex] && arr[r] >= arr[p]) { 9 midValueIndex = r; 10 }else { 11 midValueIndex = midIndex; 12 } 13 swap(arr, p, midValueIndex); 14 int pivot = arr[p]; 15 int left = p + 1; //左侧指针 16 int right = r; //右侧指针 17 while(left <= right) { 18 while(left <= right && arr[left] <= pivot) { 19 left++; 20 } 21 while(left <= right && arr[right] > pivot) { 22 right--; 23 } 24 if(left < right) { 25 swap(arr, left, right); 26 } 27 } 28 swap(arr, p, right); 29 return right; 30 }
2、绝对中值法:三点中值法也有很大的随机性,如果想要得到绝对的中值,可以通过绝对中值法来获取主元,通过将待排序数组以5个元素分为一组,取中间值,取到整个数组的各组中间值,再将这些数排序,再取中间值作为主元。因为寻找绝对中值,也会花费时间,所以使用三点中值法居多。
1 /** 2 * 获取绝对的中值数,O(N)的样子 3 */ 4 public static int getMedian(int[] arr, int p, int r) { 5 if (arr.length == 1) 6 return arr[p]; 7 int size = r - p + 1;// 数组长度 8 //每五个元素一组 9 int groupSize = (size % 5 == 0) ? (size / 5) : (size / 5 + 1); 10 //存储各小组的中值 11 int medians[] = new int[groupSize]; 12 int indexOfMedians = 0; 13 //对每一组进行插入排序 14 for (int j = 0; j < groupSize; j++) { 15 //单独处理最后一组,因为最后一组可能不满5个元素 16 if (j == groupSize - 1) { 17 InsertionSort.sort(arr, p + j * 5, r); // 排序最后一组 18 medians[indexOfMedians++] = arr[(p + j * 5 + r) / 2]; // 最后一组的中间那个 19 } else { 20 InsertionSort.sort(arr, p + j * 5, p + j * 5 + 4); // 排序非最后一组的某个组 21 medians[indexOfMedians++] = arr[p + j * 5 + 2]; // 当前组(排序后)的中间那个 22 } 23 } 24 25 return getMedian(medians, 0, medians.length - 1); 26 }
3、待排序列表较短时,用插入排序:当排序列表小于8个时,通过计算发现插入排序比快速排序的性能要好。