这篇博文详细分析了前馈神经网络的内容，它对应的函数，优化过程等等。
在上一篇博文中已经完整讲述了 SVM 的思想和原理。讲到了想用一个高度非线性的曲线作为拟合曲线。比如这个曲线可以是：
[g(x)=w_3(f_2(w_2(f_1(w_1x_1+b_1))+b2))+b3
]
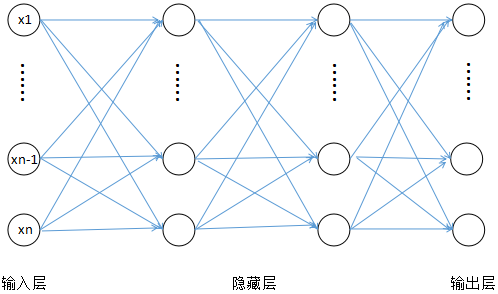
这个函数的 (x), (b) 是向量，(w) 是矩阵，最后得到的结果是向量。(f_1) 和 (f_2) 是 sigmoid 函数或者阶跃函数等非线性函数。这里就只复合三层，其实可以一直复合下去。它用一个图表示就是下面的神经网络：
神经网络示意图
这个图中输入层和输出层的每个节点其实只是输入向量 $x$ 和 $y(x)$ 的各个维度，而每个隐藏层中的节点就是一个 logistic 回归，当然，这里的激活函数可以不止是 sigmod 函数。而相邻两层间的连接线其实就是 $w$。
也就是说，这个神经网络其实就是一个复合而成的高度非线性的函数。所以其中的非线性函数是很重要的，不然的话嵌套多少层，最后的 $g(x)$ 其实还是线性函数。
那么如果直接对 $g(x)$ 构造损失函数（比如讲的平方误差之类的）也是可以的。但是优化参数时候很难，用梯度下降法之类的算法都需要求偏导，这个函数太复杂了，求起来会很麻烦。假如就写成这样一个损失函数（具体思想第一篇中讲过了~）：
$$
L(w,b) = frac{1}{n}sum_{i=1}^{n}(g(x_i) - y(x_i))^2
$$
下面的一些推导都是关于矩阵函数对矩阵或者向量的, 求导后的还是矩阵，所以链式法则的时候相乘的顺序必须是**从右向左**。
这里面 y(x) 就表示真实的标签，n 是训练样本的数量。然后就是对每个参数求偏导。因为这个是个复合函数，所以求偏导的时候需要用到链式法则。比如这里对 $w_3$ 的偏导就是：
$$frac{partial L(w,b)}{partial w_3} = frac{2}{n}sum_{i=1}^{n}frac{partial g(x_i)}{w_3}(g(x_i) - y(x_i)) = frac{2}{n}sum_{i=1}^{n}[f_2(w_2(f_1(w_1x_1+b_1))+b2)](g(x_i) - y(x_i))$$
但是如果需要求更深的某一层，比如需要求对 $w_1$ 的梯度，按照上面的方法用链式法则一层一层求偏导，最后得到关于 $w_1$ 就非常麻烦了。这里只是三层，如果层次更深情况会更加严重。但是其实我们没有必要求出关于每个参数的偏导的解析解。我们的目的是求出它们的数值。所以根据这个链式法则公式，比如在第 i 层，那么我们可能想求对于 $w_i$ 和 $b_i$ 的偏导，也就是：
$$
frac{partial J(w,b)}{partial w_i} = frac{1}{n}sum_{i=1}^{n}frac{partial (w_iF_i + b_i)}{partial w_i} frac{partial J(w,b)}{partial (w_iF_i + b_i)} = frac{1}{n}sum_{i=1}^{n}F_i frac{partial J(w,b)}{partial (w_iF_i + b_i)}
$$
其中 $F_i$ 表示 $f_i(...)$, 其中的省略号是更深的复合函数。这个的值可以把数据 $x_i$ 带进去得到。关键就是需要计算 $frac{partial J(w,b)}{partial (w_iF_i + b_i)}$。但是求导是从外向里一层一层求的，也就是如果我们知道 $frac{partial J(w,b)}{partial (w_{i+1}F_{i+1} + b_{i+1})}$，那么问题就解决了，因为可以：
$$
frac{partial J(w,b)}{partial (w_iF_i + b_i)} = frac{partial F_{i+1}}{partial (w_iF_i + b_i)}frac{partial (w_{i+1}F_{i+1} + b_{i+1})}{partial F_{i+1}}frac{partial J(w,b)}{partial (w_{i+1}F_{i+1} + b_{i+1})}
$$
这样就是一个递推式了，这里的：
$$
frac{partial (w_{i+1}F_{i+1} + b_{i+1})}{partial F_{i+1}}=w_{i+1}\
frac{partial F_{i+1}}{partial (w_iF_i + b_i)} = diag(f^{'}_{i}(w_iF_i + b_i))
$$
这里的第二个式子里面 diag 表示对角矩阵的意思，就是主对角线上的值就是 $f^{'}_{i}(w_iF_i + b_i)$ (i=1,...,m), （m 表示 z_i 的维度）。这是因为上面的函数得到的结果是向量，下面的 $(w_iF_i + b_i)$ 也是向量。而向量函数 $f(x)$ 对向量 $x$ 求偏导得到的是矩阵：
$$
egin{bmatrix}
frac{partial f_1}{partial x_1} &... &frac{partial f_m}{partial x_1} \
.&... & .\
.&... & .\
.&... & .\
frac{partial f_1}{partial x_1}&... &frac{partial f_m}{partial x_n}
end{bmatrix}
$$
在这个问题中除了对角线上的偏导之外，其它的值都是 0。
然后用 $delta_i$ 表示 $frac{partial J(w,b)}{partial (w_iF_i + b_i)}$, 那么上面这个递推式就是：
$$
delta_i=diag(f^{'}_{i}(w_iF_i + b_i))(w_{i+1}^Tdelta_{i+1})
$$
其实到这里问题就已经解决了，已经有了计算每一层 $w_i$ 和 $b_i$ 的式子，就是:
$$
frac{partial J(w,b)}{partial w_i} = frac{1}{n}sum_{i=1}^{n}F_i delta_i\
frac{partial J(w,b)}{partial b_i} = frac{1}{n}sum_{i=1}^{n} delta_i
$$
又有了关于 $delta$ 的递推式，也就是可以从 $delta_{i+1}$ 递推到 $delta_i$ ，也就可以把 $w_i$ 和 $b_i$ 算出来了。但是 $delta_{N}$ （N 为外面的一层）怎么算呢？因为 $J(w,b)$ 的形式在具体问题中是确定的，可以直接求 $delta_{N}=frac{partial J(w,b)}{partial w_NF_N + b_Ni}=frac{partial J(w,b)}{partial g(x)}$ 就行了。
这个就是神经网络中的反向传播算法。为什么叫反向传播呢？如果把这个复合函数 $L(w,b)$ 还原成神经网络的图像就比较直观了：
这里每个节点都表示一个向量，$z$ 表示没有经过激活函数的结果，$a$ 表示经过了激活函数的结果，这样把同一层的节点拆成两个过程。这里 $frac{partial J(w,b)}{partial z_i}$ 就是之前推导过程中的 $frac{partial J(w,b)}{partial (w_iF_i + b_i)}$。整个推导过程可以在这个图中更清晰的表示出来。这篇博文里调参是针对它表示的函数推导的，熟悉了的话就可以直接根据网络的图进行推导，会比较清晰（特别是 LSTM 这些复杂的网络）。关键是要找到那个递推的式子，它其实就是相邻两个层的梯度之间的关系，用链式法则联系起来。
整个流程就是对于某个训练数据 $(x_i, y_i)$, 先正向（从左往右）得到一个预测值 $f(x_i)$， 带入损失函数 $J(x, w, b)$ 中。然后用上面的递推方法反向一层一层的计算对于各层参数的梯度以及对于下一层的梯度，最后就能够算出来对于各个参数的梯度。然后利用梯度下降法等方法调整一次参数。这样一次正向，一次反向就调了一次参数。
最后那个损失函数其实有很多可以选择，交叉熵，softmax 等等。用不同的损失函数对于整个调参过程而言，就是算 $delta_N$ 的时候不同。这个 $delta$ 其实就是损失函数得到的误差，对前面每一层的输出的梯度，整个调参过程就是靠它向前传播。这个就是神经网络中的残差。
这个就是神经网络的基本流程了。但是这个算法如果是浅层的还好，一旦层数变的很多就会带来很多问题：
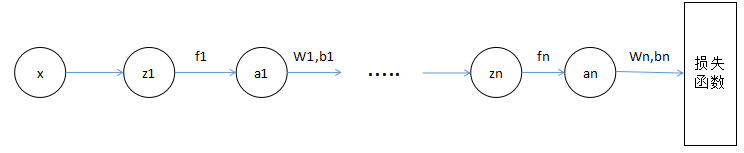
- 优化的时候计算性能要求很高。所以这个算法在发明的时候并没有特别火，现在随着计算机性能的提高，才有了商业价值。
- 梯度消失。这个是指层数太多的时候，最后几层的参数会调的比较好，所以在反向传播的时候残差会越来越小，以至于前面几层的参数很难调好。所以结果还不如用浅层的。
- 参数过多，很容易陷入局部最优解。
针对这些问题，有很多特殊的神经网络，这些网络的层数可以很深，还有各种特殊的结构。这个就是深度学习。比较常见的有循环神经网络(RNN)、卷积神经网络(CNN)、自编码器等。这些网络结构各有各的优点和用处，但是基本流程和优化方法还是跟神经网络差不多，这里就不赘述了。这个系列到这里就结束了~，自编码器、CNN 之类的以后结合 tensorflow 再写吧。
参考链接：
- 吴立德老师的视频
如需转载，请注明出处.
出处：http://www.cnblogs.com/xinchen1111/p/8793570.html
