搜索查找算法实现合集-经典搜索算法实现与分析：顺序查找，二分查找，分块查找；广度优先搜索，深度优先搜索；

本博客整理了当前经典的搜索算法的实现，并进行了简单的分析；博客中所有的代码实现位于：https://github.com/yaowenxu/codes/tree/master/搜索算法 ; 如果代码对您有帮助，希望能点击star~基于推荐和鼓励！感谢~

基本概念： 

• 搜索：就是在指定结构内，找到满足条件的关键字；这个结构可以是查找表结构，也可以是树结构也可以是图结构；
• 查找表：带有相同种类键值的元素所构成的集合；
• 关键字：元素中的某一项数字和标识，一个数据可以有很多关键字，可以通过多种维度来进行搜索；
• 主键：可以用来唯一标识数据或者记录的关键字；
• 静态查找表：查询某个特定的元素是否在表中；只做查找操作，查找过程中集合中的数据不发生变化；
• 动态查找表：在查找过程中，同时进行插入或者删除数据；
• 内查找：全部过程中都在内存中进行，为内查找；
• 外查找：全部过程中需要访问外存，为外查找；
• 性能评价：ASL(Average Search Length)，平均比较长度；表示在查找过程中对关键字的需要执行的平均比较长度（平均比较次数），来进行评价算法性能优劣；
• 查找算法选取：判断当前数据的组织结构，是线性表还是树结构还是图结构；如果是顺序表，还要考虑表格中的数据是否有序；

顺序查找：顺序查找的思想是从左到右依次进行扫描比较，如果满足指定的查找条件则查找成功，若到末尾还未找到，则数组中无满足结构，适合与线性表；数据可以有序也可以无序；

#define DEBUG 1
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
void printarray(vector<int> &arr);

void seqsearch(vector<int> &arr, int v=500){
    cout << "开始查找数据：" << v << endl;
    bool flag =  true;
    for (int i = 0; i < arr.size(); i++)
    {
        if(arr[i] == v){
            cout << "满足索引：" << i << endl;
            flag = false;
        }
    }
    if (flag)
    {
        cout << "无满足数据！" << endl;
    }
}

// 打印函数；
void printarray(vector<int> &arr){
    for(int i = 0; i < arr.size(); i++){
        cout << arr[i] << " ";
    }
    cout << endl;
}

int main(){
    vector<int> arr; 
    freopen("in.txt", "r", stdin); // 重定向到输入 
    int i = 0; 
    int tmp; 
    while (cin >> tmp)
    {   
        arr.push_back(tmp);
        // cout << inarray[i] << endl;
        i++;
    }
    int num =  i;
    cout << "输入数据：" << endl;
    printarray(arr);
    cout << endl;
    if (DEBUG){
        cout << "查找过程：" << endl;
    }

    // 顺序查找
    seqsearch(arr);
    return 0;
}

bash-3.2$ c++ 顺序查找.cc;./a.out
输入数据：
1 2 3 500 9 7 6 500 1 2 

查找过程：
开始查找数据：500
满足索引：3
满足索引：7

算法复杂度：如果只查找一个元素，第一个元素满足情况为1；最后一个满足情况，需要比较n次；
平均时间复杂度：ASL =  (n+...+1)/n = (n+1)/2，O(n);

二分查找：二分查找又称为折半查找；思想是将查找的关键字与中间记录关键字进行比较，如果相等则查找结束；若不相等，比较自身和中间元素的大小，如果小于中间元素，则在左半部递归查找，如果大于中间元素则在右半部递归查找；该算法适合有序顺序表的查找；二分查找使用了一种减治的思想；

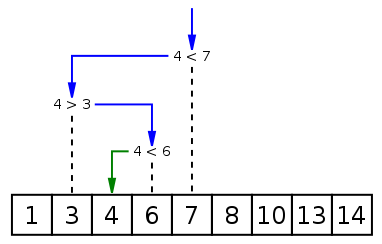
#define DEBUG 1
#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
void printarray(vector<int> &arr);

// 递归实现，找出其中一个满足的方案；如果需要找出所有的满足方案，只要先找出其中一个满足方案，然后在其左右顺序搜索就可以了；(因为数组是排序好的)
void binsearch(vector<int> &arr, int start, int end, int v=900){
    if(DEBUG){
        cout << "s=" << start << " " << "e=" << end << endl;
    }
    if(end < start){
        cout << "无满足数据！" << endl;
        return;
    }
    int mid = (start+end)/2;
    if(arr[mid] == v){
        cout << "满足索引：" << mid << endl;
        return;
    }
    if(arr[mid] < v){
        binsearch(arr, mid+1, end);
    }
    if(arr[mid] > v){
        binsearch(arr, start, mid-1);
    }
}

// 非递归实现，非递归实现使用循环实现，注意循环的出口；以及索引的更新；
void binsearch_2(vector<int> &arr, int v=900){
    int start =  0;
    int end = arr.size()-1;
    int flag = true;
    //使用 do-while 来进行循环
    do {
        int mid = (start+end)/2;
        if(DEBUG){
            cout << "s=" << start << " " << "e=" << end << endl;
        }
        if (arr[mid]==v){
            cout << "满足索引：" << mid << endl;
            flag = false;
            break;
        }
        if (arr[mid] > v){
            end = mid-1;
        }
        if (arr[mid] < v){
            start = mid+1;
        }
    } while (end >= start);
    if(flag){
        cout << "无满足数据！" << endl;
    }
}

// 打印函数；
void printarray(vector<int> &arr){
    for(int i = 0; i < arr.size(); i++){
        cout << arr[i] << " ";
    }
    cout << endl;
}

int main(){
    vector<int> arr; 
    freopen("in.txt", "r", stdin); // 重定向到输入 
    int i = 0; 
    int tmp; 
    while (cin >> tmp)
    {   
        arr.push_back(tmp);
        // cout << inarray[i] << endl;
        i++;
    }
    int num =  i;
    sort(arr.begin(), arr.end());
    cout << "输入数据：" << endl;
    printarray(arr);
    cout << endl;
    if (DEBUG){
        cout << "查找过程：" << endl;
    }

    // 顺序查找
    cout << "binsearch-递归：" << endl;
    binsearch(arr, 0, arr.size()-1);
    cout << "binsearch-非递归：" << endl;
    binsearch_2(arr);
    return 0;
}

bash-3.2$ c++ 二分查找.cc; ./a.out
输入数据：
1 2 4 5 7 8 300 900 

查找过程：
binsearch-递归：
s=0 e=7
s=4 e=7
s=6 e=7
s=7 e=7
满足索引：7
binsearch-非递归：
s=0 e=7
s=4 e=7
s=6 e=7
s=7 e=7
满足索引：7

平均时间复杂度：查找区间可以看作，中间为树的根；左区间为左子树，右区间为右子树，整个查找过程中为二叉树；平均查找就是从二叉树的深度，为 O(logn);但一般数据使用二分查找，要求数据有序，如果数据无序，则先需要使用排序算法对无序数组进行排序；本实现使用的是 sort函数；当然你可以自行实现；

分块查找：分块查找，分块就是把数据分为很多块；块内的数据是没有顺序的；块与块之间是有序的；左块中的元素小于右块中元素的最小值；分块查找由分块有序的线性表和有序的索引表构成；索引表记录了每个块的最大关键字和块的起始位置；在查找过程中，先使用二分查找定位到对应的块；然后再在块中进行顺序搜索；分块查找支持动态数据查找；

#include <iostream>
using namespace std;

int seqtable[20] = {8, 14, 6, 9, 10, 22, 34, 18, 19, 31, 40, 38, 54, 66, 46, 71, 78, 68, 80, 85}; // 顺序表
int indextable[4][2] = {{14, 0},{34, 5},{66, 10},{85, 15}}; // 索引表 

void blocksearch1(int v = 85){
    // 二分查找；
    int start = 0;
    int stop = 3;
    // 顺序搜索的范围，该变量由二分搜索查表确定
    int s = 0;
    int e = 20;
    do{
        int mid =  (start+stop)/2;
        cout << "二分查找前：" << "start:" << start << " mid:" << mid << " stop:" << stop << " s=" << s << " e=" << e << endl;
        if(indextable[mid][0] < v){
            start = mid+1;
            if (mid == 3){
                cout << "无满足数据！" << endl;
                return;
            }
            s =  indextable[mid+1][1];
        }
        if(indextable[mid][0] >= v){
            stop = mid-1;
            if (mid < 3){
                e =  indextable[mid+1][1];
            }
        }
        cout << "二分查找后：" << "start:" << start << " mid:" << mid << " stop:" << stop << " s=" << s << " e=" << e << endl;
    }while(stop >= start);
    
    // 顺序搜索
    cout << "顺序搜索区间: " << "s=" << s << " e=" << e << endl; 
    int flag = true;
    for (int i = s; i < e; i++){
        if(seqtable[i] ==  v){
            cout << "满足索引：" << i << endl;
            flag = false;
            break;
        }
    }
    if (flag){
        cout << "无满足数据！" << endl;
    }
}

void blocksearch2(int v = 85){
    // 二分查找；
    int start = 0;
    int stop = 3;
    // 顺序搜索的范围，该变量由二分搜索查表确定
    int s = 0;
    int e = 20;
    do{
        int mid =  (start+stop)/2;
        cout << "二分查找前：" << "start:" << start << " mid:" << mid << " stop:" << stop << " s=" << s << " e=" << e << endl;
        if(indextable[mid][0] == v){  // 加入此判断，可以过早终止；
            s = indextable[mid][1];
            if (mid < 3){
                e =  indextable[mid+1][1];
            }
            break;
        }
        if(indextable[mid][0] < v){   // 加入此判断可以过早终止；
            start = mid+1;
            if (mid == 3){
                cout << "无满足数据！" << endl;
                return;
            }
            s =  indextable[mid+1][1];
        }
        if(indextable[mid][0] > v){
            stop = mid-1;
            if (mid < 3){
                e =  indextable[mid+1][1];
            }
        }
        cout << "二分查找后：" << "start:" << start << " mid:" << mid << " stop:" << stop << " s=" << s << " e=" << e << endl;
    }while(stop >= start);
    
    // 顺序搜索
    cout << "顺序搜索区间: " << "s=" << s << " e=" << e << endl; 
    int flag = true;
    for (int i = s; i < e; i++){
        if(seqtable[i] ==  v){
            cout << "满足索引：" << i << endl;
            flag = false;
            break;
        }
    }
    if (flag){
        cout << "无满足数据！" << endl;
    }
}

int main(){
    cout << "分块查找1:" << endl;
    blocksearch1();
    cout << endl;
    cout << "分块查找2:" << endl;
    blocksearch2();
}

bash-3.2$ c++ 分块查找.cc; ./a.out
分块查找1:
二分查找前：start:0 mid:1 stop:3 s=0 e=20
二分查找后：start:2 mid:1 stop:3 s=10 e=20
二分查找前：start:2 mid:2 stop:3 s=10 e=20
二分查找后：start:3 mid:2 stop:3 s=15 e=20
二分查找前：start:3 mid:3 stop:3 s=15 e=20
二分查找后：start:3 mid:3 stop:2 s=15 e=20
顺序搜索区间: s=15 e=20
满足索引：19

分块查找2:
二分查找前：start:0 mid:1 stop:3 s=0 e=20
二分查找后：start:2 mid:1 stop:3 s=10 e=20
二分查找前：start:2 mid:2 stop:3 s=10 e=20
二分查找后：start:3 mid:2 stop:3 s=15 e=20
二分查找前：start:3 mid:3 stop:3 s=15 e=20
顺序搜索区间: s=15 e=20
满足索引：19

算法时间复杂度：块间使用二分查找进行查找；块内使用顺序搜索进行查找；效率介于顺序查找和二分查找之间；
平均查找长度：二分查找 > 分块查找 > 顺序查找；
适用性：顺序搜索无条件限制，二分查找要求数据有序；分块查找要求分块有序；
存储结构：顺序查找和分块查找适用于顺序表和链表；二分查找适用于顺序表；
分块查找优点：分块查找效率介于顺序查找和二分查找之间，可以用于动态数据查找；

广度优先搜索(BFS)：Breadth First Search; 从树的根开始，从上打下，从左到右遍历树的节点；

深度优先搜索(DFS): Depth First Search; 沿着树的深度优先遍历树的节点，直到到达叶子节点，再进行回溯；根绝根节点遍历顺序的不同，又分为先序，中序和后序遍历；

关于深度优先搜索和广度优先搜索，在经典数据结构实现与分析树结构部分进行详细讲解；

保持更新，转载请注明出处；更多内容请关注cnblogs.com/xuyaowen;

参考链接：

七大查找算法（Python）

几种常见的搜索算法 

程序员的内功——数据结构和算法系列 

排序与搜索