最长公共子序列（LCS）

题目描述：

　　传送门 

题解：最长公共子序列是一个经典的dp问题。核心的递推公式如下图，根据下面的递推式子便能写出解决的代码。

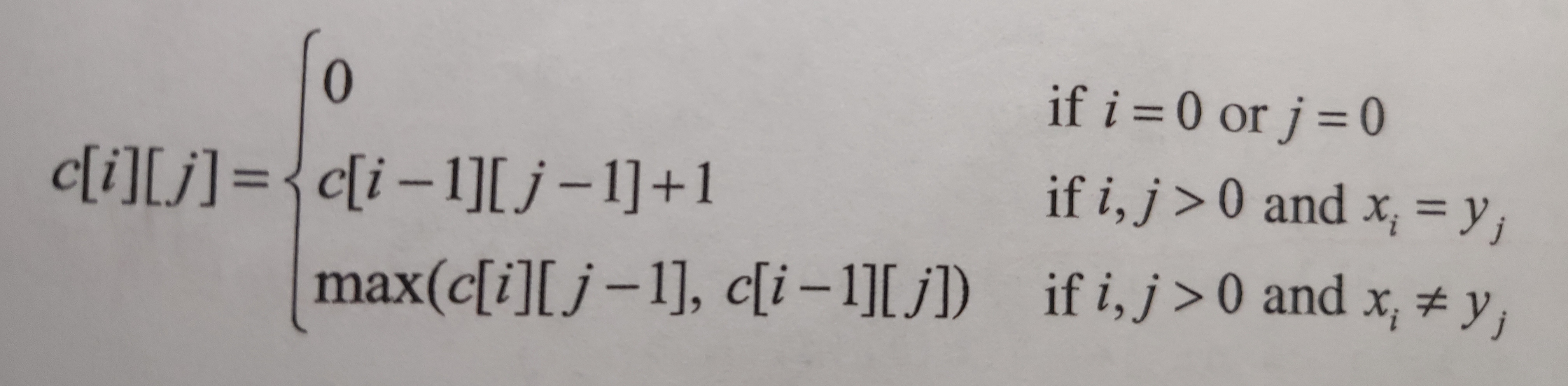
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;

int num[10000][10000]={0};
int a[100000];
int b[100000];
//根据递推公式可判断是从前往后推  递推方向的判断很重要 
int n=0;
int main(){
    cin>>n;
    
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    for(int i=1;i<=n;i++){
        cin>>b[i];
    }
    
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(a[i]==b[j]){            //相当于xi==yi时 
                num[i][j]=num[i-1][j-1]+1;
            }else{
                num[i][j]=max(num[i-1][j],num[i][j-1]);        //相当于xi不等于yi时 
            }
        }
    }
    
    cout<<num[n][n];
    
    return 0;
}

对于这个题而言，朴素算法是n^2的，会被10^5卡死，所以我么可以考虑nlogn的做法。

下面的做法是将求解最长公共子序列问题转换为最长上升子序列问题，从而提高效率。

比如序列a、b分别为：

a: 5 3 2 1 4

b: 3 5 4 2 1

首先第一步以序列a为标准，即将序列a换成1 2 3 4 5（1~n）的形式。因此可以看见在序列a中有如下对应关系：

5-1  3-2  2-3  1-4  4-5（m-n代表m换成了n，这种对应关系同样也要用在b序列）

此时b序列变成2 1 5 3 4。

由于a序列是一个绝对的上升序列（1~n），因此要找变换后的两个序列的最长公共子序列变成了找在b序列中的最长上升子序列（因为a中只有上升，b中有上升则一定会与a中的部分元素对应）。比如这里b的最长上升子序列变成了1 3 4。从而传统的LCS问题转换成了一个不用LCS求解而用LIS求解的问题。

那么接下来的问题是如何求解nlogn的LIS问题？

具体思路见：https://www.cnblogs.com/xwh-blogs/p/12867960.html

#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
#define re register

int a[100005];
int b[100005];
int mapp[100005];
int index[100005];        //专门用于存第2个序列的下标数组，减少搜索的时间复杂度 
//思考递归还是循环递推  10^5比较大 递归不好说 
//根据递推公式可判断是从前往后推  递推方向的判断很重要 
int n=0;
int main(){
    int maxlen[100005]={0};
    int len=0;
    cin>>n;
    for(re int i=1;i<=n;i++){
        cin>>a[i];
    }
    for(re int i=1;i<=n;i++){
        cin>>b[i];
        index[b[i]]=i;
    }
    
    for(int i=1;i<=n;i++){
        mapp[index[a[i]]]=i;
    }
    //现在变成一个求最长上升子序列的问题 
    maxlen[1]=mapp[1];        //第一个数直接放入maxlen中
    len=1;
    for(re int i=2;i<=n;i++){        //从第2个数开始搜起 ;
        if(maxlen[len]<mapp[i]){        //maxlen[len]是当前maxlen数组最末的一个数 
            len++;
            maxlen[len]=mapp[i];
        }else{
            int *pos;
            pos=lower_bound(maxlen+1,maxlen+1+len,mapp[i]);    //返回的是地址 
            *pos=mapp[i];                //加1是因为下标从1开始 
        }
    }
    cout<<len;
    return 0;
}