普通的二叉搜索树作为数据存储工具有重要的优势:可以快速地找到一个给定关键字的数据项,并且可以快速地插入和删除数据项。其他的数据存储结构,例如数组、有序数组以及链表,执行这些操作却很慢。因此,二叉搜索树似乎是理想的数据存储结构。
如果树中插入的是随机数据,则执行效果很好。但是,如果插入的是有序的数据或者是逆序的数据,速度就变得特别慢。因为当插入的数值有序时,二叉树就是非平衡的了。而对于非平衡树,它的快速查找(插入,删除)指定的数据项的能力就丧失了。O(log(N))-->O(N)
解决非平衡树问题的方法:红-黑树,它是增加了某些特点的二叉搜索树。
红黑规则:
当插入(或者删除)一个新节点时,必须要遵循的一定的规则,它们被称为红-黑规则。如果遵循这些规则,树就是平衡的。
1、每一个节点不是红色的就是黑色的。
2、根节点是黑色的。
3、每个叶子节点(NILL)是黑色的。【这里的叶节点是指为空的叶子节点】
4、如果节点是红色的,则它的子节点必须是黑色的。
5、对于任意结点而言,其到叶结点树尾端NIL指针的每条路径都包含相同数目的黑结点。【确保没有一条路径会比其他路径长出两倍,因而,红黑树是相对是接近平衡的二叉树】
红黑树的时间复杂度:
一颗含有N个节点的红黑树的高度至多为2log(N+1)
因为每个节点到叶子节点(null),黑色节点是相同的,它的一个孩子的高度最多是它的另一个孩子高度的2倍。假设是平衡树,则树高为log(N),所以红黑树的高度最多是它的两倍。
红黑树的基本操作(一)左旋和右旋
红黑树的基本操作是添加,删除。在对红黑树进行添加或删除之后,都会用到旋转方法。添加或删除红黑树中的节点之后,红黑树就发生了变化,可能不满足红黑树的5条性质,也就不再是一颗红黑树了,而是一颗普通的树。而通过旋转,可以使这棵树重新成为红黑树。简单点说,旋转的目的是让树保持红黑树的特性。
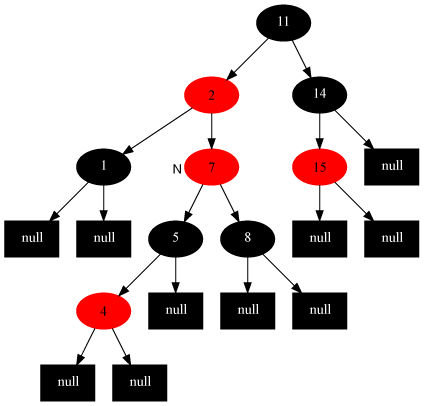
红黑树示意图如下:
红黑树的应用
红黑树的应用比较广泛,主要是用它来存储有序的数据,它的时间复杂度是O(lgn),效率非常之高。
例如,Java集合中的TreeSet和TreeMap,C++ STL中的set、map,以及Linux虚拟内存的管理,都是通过红黑树去实现的。
红黑树的基本操作(一) 左旋和右旋
红黑树的基本操作是添加、删除。在对红黑树进行添加或删除之后,都会用到旋转方法。为什么呢?道理很简单,添加或删除红黑树中的节点之后,红黑树就发生了变化,可能不满足红黑树的5条性质,也就不再是一颗红黑树了,而是一颗普通的树。而通过旋转,可以使这颗树重新成为红黑树。简单点说,旋转的目的是让树保持红黑树的特性。
旋转包括两种:左旋 和 右旋。下面分别对它们进行介绍。
1. 左旋
对x进行左旋,意味着"将x变成一个左节点"。
左旋的伪代码《算法导论》:参考上面的示意图和下面的伪代码,理解“红黑树T的节点x进行左旋”是如何进行的。
LEFT-ROTATE(T, x) 01 y ← right[x] // 前提:这里假设x的右孩子为y。下面开始正式操作 02 right[x] ← left[y] // 将 “y的左孩子” 设为 “x的右孩子”,即 将β设为x的右孩子 03 p[left[y]] ← x // 将 “x” 设为 “y的左孩子的父亲”,即 将β的父亲设为x 04 p[y] ← p[x] // 将 “x的父亲” 设为 “y的父亲” 05 if p[x] = nil[T] 06 then root[T] ← y // 情况1:如果 “x的父亲” 是空节点,则将y设为根节点 07 else if x = left[p[x]] 08 then left[p[x]] ← y // 情况2:如果 x是它父节点的左孩子,则将y设为“x的父节点的左孩子” 09 else right[p[x]] ← y // 情况3:(x是它父节点的右孩子) 将y设为“x的父节点的右孩子” 10 left[y] ← x // 将 “x” 设为 “y的左孩子” 11 p[x] ← y // 将 “x的父节点” 设为 “y”
理解左旋之后,看看下面一个更鲜明的例子。你可以先不看右边的结果,自己尝试一下。
2. 右旋
对x进行左旋,意味着"将x变成一个左节点"。
右旋的伪代码《算法导论》:参考上面的示意图和下面的伪代码,理解“红黑树T的节点y进行右旋”是如何进行的。
RIGHT-ROTATE(T, y) 01 x ← left[y] // 前提:这里假设y的左孩子为x。下面开始正式操作 02 left[y] ← right[x] // 将 “x的右孩子” 设为 “y的左孩子”,即 将β设为y的左孩子 03 p[right[x]] ← y // 将 “y” 设为 “x的右孩子的父亲”,即 将β的父亲设为y 04 p[x] ← p[y] // 将 “y的父亲” 设为 “x的父亲” 05 if p[y] = nil[T] 06 then root[T] ← x // 情况1:如果 “y的父亲” 是空节点,则将x设为根节点 07 else if y = right[p[y]] 08 then right[p[y]] ← x // 情况2:如果 y是它父节点的右孩子,则将x设为“y的父节点的左孩子” 09 else left[p[y]] ← x // 情况3:(y是它父节点的左孩子) 将x设为“y的父节点的左孩子” 10 right[x] ← y // 将 “y” 设为 “x的右孩子” 11 p[y] ← x // 将 “y的父节点” 设为 “x”
理解右旋之后,看看下面一个更鲜明的例子。你可以先不看右边的结果,自己尝试一下。
旋转总结:
(01) 左旋 和 右旋 是相对的两个概念,原理类似。理解一个也就理解了另一个。
(02) 下面谈谈如何区分 左旋 和 右旋。
在实际应用中,若没有彻底理解 左旋 和 右旋,可能会将它们混淆。下面谈谈我对如何区分 左旋 和 右旋 的理解。
左旋示例图(以x为节点进行左旋):
z
x /
/ --(左旋)--> x
y z /
y
对x进行左旋,意味着,将“x的右孩子”设为“x的父亲节点”;即,将 x变成了一个左节点(x成了为z的左孩子)!。 因此,左旋中的“左”,意味着“被旋转的节点将变成一个左节点”。
右旋示例图(以x为节点进行右旋):
y
x
/ --(右旋)--> x
y z
z
对x进行右旋,意味着,将“x的左孩子”设为“x的父亲节点”;即,将 x变成了一个右节点(x成了为y的右孩子)! 因此,右旋中的“右”,意味着“被旋转的节点将变成一个右节点”。
红黑树的基本操作(二) 添加
将一个节点插入到红黑树中,需要执行哪些步骤呢?首先,将红黑树当作一颗二叉查找树,将节点插入;然后,将节点着色为红色;最后,通过旋转和重新着色等方法来修正该树,使之重新成为一颗红黑树。详细描述如下:
第一步: 将红黑树当作一颗二叉查找树,将节点插入。
红黑树本身就是一颗二叉查找树,将节点插入后,该树仍然是一颗二叉查找树。也就意味着,树的键值仍然是有序的。此外,无论是左旋还是右旋,若旋转之前这棵树是二叉查找树,旋转之后它一定还是二叉查找树。这也就意味着,任何的旋转和重新着色操作,都不会改变它仍然是一颗二叉查找树的事实。
第二步:将插入的节点着色为"红色"。
第三步: 通过一系列的旋转或着色等操作,使之重新成为一颗红黑树。
第二步中,将插入节点着色为"红色"之后,不会违背"特性(5)"。那它到底会违背哪些特性呢?
对于"特性(1)",显然不会违背了。因为我们已经将它涂成红色了。
对于"特性(2)",显然也不会违背。在第一步中,我们是将红黑树当作二叉查找树,然后执行的插入操作。而根据二叉查找数的特点,插入操作不会改变根节点。所以,根节点仍然是黑色。
对于"特性(3)",显然不会违背了。这里的叶子节点是指的空叶子节点,插入非空节点并不会对它们造成影响。
对于"特性(4)",是有可能违背的!
那接下来,想办法使之"满足特性(4)",就可以将树重新构造成红黑树了。
下面看看代码到底是怎样实现这三步的。
添加操作的伪代码《算法导论》
RB-INSERT(T, z) 01 y ← nil[T] // 新建节点“y”,将y设为空节点。 02 x ← root[T] // 设“红黑树T”的根节点为“x” 03 while x ≠ nil[T] // 找出要插入的节点“z”在二叉树T中的位置“y” 04 do y ← x 05 if key[z] < key[x] 06 then x ← left[x] 07 else x ← right[x] 08 p[z] ← y // 设置 “z的父亲” 为 “y” 09 if y = nil[T] 10 then root[T] ← z // 情况1:若y是空节点,则将z设为根 11 else if key[z] < key[y] 12 then left[y] ← z // 情况2:若“z所包含的值” < “y所包含的值”,则将z设为“y的左孩子” 13 else right[y] ← z // 情况3:(“z所包含的值” >= “y所包含的值”)将z设为“y的右孩子” 14 left[z] ← nil[T] // z的左孩子设为空 15 right[z] ← nil[T] // z的右孩子设为空。至此,已经完成将“节点z插入到二叉树”中了。 16 color[z] ← RED // 将z着色为“红色” 17 RB-INSERT-FIXUP(T, z) // 通过RB-INSERT-FIXUP对红黑树的节点进行颜色修改以及旋转,让树T仍然是一颗红黑树
结合伪代码以及为代码上面的说明,先理解RB-INSERT。理解了RB-INSERT之后,我们接着对 RB-INSERT-FIXUP的伪代码进行说明。
添加修正操作的伪代码《算法导论》
RB-INSERT-FIXUP(T, z) 01 while color[p[z]] = RED // 若“当前节点(z)的父节点是红色”,则进行以下处理。 02 do if p[z] = left[p[p[z]]] // 若“z的父节点”是“z的祖父节点的左孩子”,则进行以下处理。 03 then y ← right[p[p[z]]] // 将y设置为“z的叔叔节点(z的祖父节点的右孩子)” 04 if color[y] = RED // Case 1条件:叔叔是红色 05 then color[p[z]] ← BLACK ▹ Case 1 // (01) 将“父节点”设为黑色。 06 color[y] ← BLACK ▹ Case 1 // (02) 将“叔叔节点”设为黑色。 07 color[p[p[z]]] ← RED ▹ Case 1 // (03) 将“祖父节点”设为“红色”。 08 z ← p[p[z]] ▹ Case 1 // (04) 将“祖父节点”设为“当前节点”(红色节点) 09 else if z = right[p[z]] // Case 2条件:叔叔是黑色,且当前节点是右孩子 10 then z ← p[z] ▹ Case 2 // (01) 将“父节点”作为“新的当前节点”。 11 LEFT-ROTATE(T, z) ▹ Case 2 // (02) 以“新的当前节点”为支点进行左旋。 12 color[p[z]] ← BLACK ▹ Case 3 // Case 3条件:叔叔是黑色,且当前节点是左孩子。(01) 将“父节点”设为“黑色”。 13 color[p[p[z]]] ← RED ▹ Case 3 // (02) 将“祖父节点”设为“红色”。 14 RIGHT-ROTATE(T, p[p[z]]) ▹ Case 3 // (03) 以“祖父节点”为支点进行右旋。 15 else (same as then clause with "right" and "left" exchanged) // 若“z的父节点”是“z的祖父节点的右孩子”,将上面的操作中“right”和“left”交换位置,然后依次执行。 16 color[root[T]] ← BLACK
根据被插入节点的父节点的情况,可以将"当节点z被着色为红色节点,并插入二叉树"划分为三种情况来处理。
① 情况说明:被插入的节点是根节点。
处理方法:直接把此节点涂为黑色。
② 情况说明:被插入的节点的父节点是黑色。
处理方法:什么也不需要做。节点被插入后,仍然是红黑树。
③ 情况说明:被插入的节点的父节点是红色。
处理方法:那么,该情况与红黑树的"特性(5)"相冲突。这种情况下,被插入节点是一定存在非空祖父节点的;进一步的讲,被插入节点也一定存在叔叔节点(即使叔叔节点为空,我们也视之为存在,空节点本身就是黑色节点)。理解这点之后,我们依据"叔叔节点的情况",将这种情况进一步划分为3种情况(Case)。
| 现象说明 | 处理策略 | |
| Case 1 | 当前节点的父节点是红色,且当前节点的祖父节点的另一个子节点(叔叔节点)也是红色。 |
(01) 将“父节点”设为黑色。 |
| Case 2 | 当前节点的父节点是红色,叔叔节点是黑色,且当前节点是其父节点的右孩子 |
(01) 将“父节点”作为“新的当前节点”。 |
| Case 3 | 当前节点的父节点是红色,叔叔节点是黑色,且当前节点是其父节点的左孩子 |
(01) 将“父节点”设为“黑色”。 |
上面三种情况(Case)处理问题的核心思路都是:将红色的节点移到根节点;然后,将根节点设为黑色。下面对它们详细进行介绍。
1. (Case 1)叔叔是红色
1.1 现象说明
当前节点(即,被插入节点)的父节点是红色,且当前节点的祖父节点的另一个子节点(叔叔节点)也是红色。
1.2 处理策略
(01) 将"父节点"设为黑色。
(02) 将"叔叔节点"设为黑色。
(03) 将"祖父节点"设为"红色"。
(04) 将"祖父节点"设为"当前节点"(红色节点);即,之后继续对"当前节点"进行操作。
下面谈谈为什么要这样处理。(建议理解的时候,通过下面的图进行对比)
"当前节点"和"父节点"都是红色,违背"特性(4)"。所以,将"父节点"设置"黑色"以解决这个问题。
但是,将"父节点"由"红色"变成"黑色"之后,违背了"特性(5)":因为,包含"父节点"的分支的黑色节点的总数增加了1。 解决这个问题的办法是:将"祖父节点"由"黑色"变成红色,同时,将"叔叔节点"由"红色"变成"黑色"。关于这里,说明几点:第一,为什么"祖父节点"之前是黑色?这个应该很容易想明白,因为在变换操作之前,该树是红黑树,"父节点"是红色,那么"祖父节点"一定是黑色。 第二,为什么将"祖父节点"由"黑色"变成红色,同时,将"叔叔节点"由"红色"变成"黑色";能解决"包含'父节点'的分支的黑色节点的总数增加了1"的问题。这个道理也很简单。"包含'父节点'的分支的黑色节点的总数增加了1"同时也意味着 "包含'祖父节点'的分支的黑色节点的总数增加了1",既然这样,我们通过将"祖父节点"由"黑色"变成"红色"以解决"包含'祖父节点'的分支的黑色节点的总数增加了1"的问题; 但是,这样处理之后又会引起另一个问题“包含‘叔叔’节点的分支的黑色节点的总数减少了1",现在我们已知"叔叔节点"是"红色",将"叔叔节点"设为"黑色"就能解决这个问题。 所以,将"祖父节点"由"黑色"变成红色,同时,将"叔叔节点"由"红色"变成"黑色";就解决了该问题。
按照上面的步骤处理之后:当前节点、父节点、叔叔节点之间都不会违背红黑树特性,但祖父节点却不一定。若此时,祖父节点是根节点,直接将祖父节点设为"黑色",那就完全解决这个问题了;若祖父节点不是根节点,那我们需要将"祖父节点"设为"新的当前节点",接着对"新的当前节点"进行分析。
1.3 示意图
红黑树由之前的:
变化成:
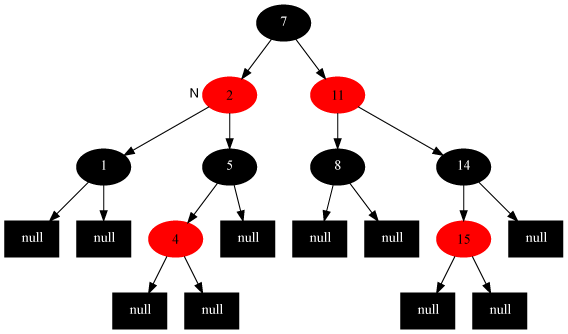
2. (Case 2)叔叔是黑色,且当前节点是右孩子
2.1 现象说明
当前节点(7)的父节点是红色,叔叔节点(14)是黑色,且当前节点是其父节点的右孩子
2.2 处理策略
1、将"父节点"作为"新的当前节点"。
2、以"新的当前节点"为支点进行左旋。
下面谈谈为什么要这样处理。(建议理解的时候,通过下面的图进行对比)
首先,将"父节点"作为"新的当前节点";接着,以"新的当前节点"为支点进行左旋。 为了便于理解,我们先说明第(02)步,再说明第(01)步;为了便于说明,我们设置"父节点"的代号为F(Father),"当前节点"的代号为S(Son)。
为什么要"以F为支点进行左旋"呢?根据已知条件可知:S是F的右孩子。而之前我们说过,我们处理红黑树的核心思想:将红色的节点移到根节点;然后,将根节点设为黑色。既然是"将红色的节点移到根节点",那就是说要不断的将破坏红黑树特性的红色节点上移(即向根方向移动)。 而S又是一个右孩子,因此,我们可以通过F"左旋"来将S上移!
按照上面的步骤(以F为支点进行左旋)处理之后:若S变成了根节点,那么直接将其设为"黑色",就完全解决问题了;若S不是根节点,那我们需要执行步骤(01),即"将F设为'新的当前节点'"。那为什么不继续以S为新的当前节点继续处理,而需要以F为新的当前节点来进行处理呢?这是因为"左旋"之后,F变成了S的"子节点",即S变成了F的父节点;而我们处理问题的时候,需要从下至上(由叶到根)方向进行处理;也就是说,必须先解决"孩子"的问题,再解决"父亲"的问题;所以,我们执行步骤(01):将"父节点"(2)作为"新的当前节点"。
2.2 示意图
所以红黑树由之前的:
变化成:
3. (Case 3)叔叔是黑色,且当前节点是左孩子
3.1 现象说明
当前节点(2)的父节点(7)是红色,叔叔节点(14)是黑色,且当前节点是其父节点的左孩子
3.2 处理策略
(01) 将"父节点"设为"黑色"。
(02) 将"祖父节点"设为"红色"。
(03) 以"祖父节点"为支点进行右旋。
下面谈谈为什么要这样处理。(建议理解的时候,通过下面的图进行对比)
为了便于说明,我们设置"当前节点"为S(Original Son),"兄弟节点"为B(Brother),"叔叔节点"为U(Uncle),"父节点"为F(Father),祖父节点为G(Grand-Father)。
S和F都是红色,违背了红黑树的“特性(4)”,我们可以将F由“红色”变为“黑色”,就解决了“违背‘特性(4)’”的问题;但却引起了其它问题:违背特性(5),因为将F由红色改为黑色之后,所有经过F的分支的黑色节点的个数增加了1。那我们如何解决"所有经过F的分支的黑色节点的个数增加了1"的问题呢? 我们可以通过"将G由黑色变成红色",同时"以G为支点进行右旋"来解决。
2.3 示意图
所以红黑树由之前的:
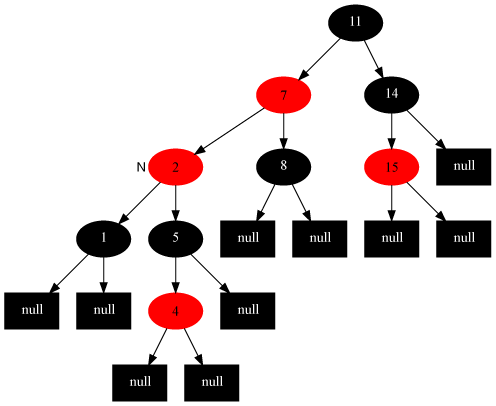
变化成:
红黑树的基本操作(三) 删除
将红黑树内的某一个节点删除。需要执行的操作依次是:首先,将红黑树当作一颗二叉查找树,将该节点从二叉查找树中删除;然后,通过"旋转和重新着色"等一系列来修正该树,使之重新成为一棵红黑树。详细描述如下:
第一步:将红黑树当作一颗二叉查找树,将节点删除。
这和"删除常规二叉查找树中删除节点的方法是一样的"。分3种情况:
① 被删除节点没有儿子,即为叶节点。那么,直接将该节点删除就OK了。
② 被删除节点只有一个儿子。那么,直接删除该节点,并用该节点的唯一子节点顶替它的位置。
③ 被删除节点有两个儿子。那么,先找出它的后继节点(右子树的最小值的那个节点,该节点要么没有孩子,要么只有一个右孩子,如果有左孩子,那么它的左孩子就是子树最小值了);然后把"它的后继节点的内容"复制给"该节点的内容";之后,删除"它的后继节点"。在这里,后继节点相当于替身,在将后继节点的内容复制给"被删除节点"之后,再将后继节点删除。这样就巧妙的将问题转换为"删除后继节点"的情况了,下面就考虑后继节点。 在"被删除节点"有两个非空子节点的情况下,它的后继节点不可能是双子非空。既然"的后继节点"不可能双子都非空,就意味着"该节点的后继节点"要么没有儿子,要么只有一个儿子。若没有儿子,则按"情况① "进行处理;若只有一个儿子,则按"情况② "进行处理。
第二步:通过"旋转和重新着色"等一系列来修正该树,使之重新成为一棵红黑树。
因为"第一步"中删除节点之后,可能会违背红黑树的特性。所以需要通过"旋转和重新着色"来修正该树,使之重新成为一棵红黑树。
删除操作的伪代码《算法导论》
RB-DELETE(T, z) 01 if left[z] = nil[T] or right[z] = nil[T] 02 then y ← z // 若“z的左孩子” 或 “z的右孩子”为空,则将“z”赋值给 “y”; 03 else y ← TREE-SUCCESSOR(z) // 否则,将“z的后继节点”赋值给 “y”。 04 if left[y] ≠ nil[T] 05 then x ← left[y] // 若“y的左孩子” 不为空,则将“y的左孩子” 赋值给 “x”; 06 else x ← right[y] // 否则,“y的右孩子” 赋值给 “x”。 07 p[x] ← p[y] // 将“y的父节点” 设置为 “x的父节点” 08 if p[y] = nil[T] 09 then root[T] ← x // 情况1:若“y的父节点” 为空,则设置“x” 为 “根节点”。 10 else if y = left[p[y]] 11 then left[p[y]] ← x // 情况2:若“y是它父节点的左孩子”,则设置“x” 为 “y的父节点的左孩子” 12 else right[p[y]] ← x // 情况3:若“y是它父节点的右孩子”,则设置“x” 为 “y的父节点的右孩子” 13 if y ≠ z 14 then key[z] ← key[y] // 若“y的值” 赋值给 “z”。注意:这里只拷贝z的值给y,而没有拷贝z的颜色!!! 15 copy y's satellite data into z 16 if color[y] = BLACK 17 then RB-DELETE-FIXUP(T, x) // 若“y为黑节点”,则调用 18 return y
结合伪代码以及为代码上面的说明,先理解RB-DELETE。理解了RB-DELETE之后,接着对 RB-DELETE-FIXUP的伪代码进行说明
RB-DELETE-FIXUP(T, x) 01 while x ≠ root[T] and color[x] = BLACK 02 do if x = left[p[x]] 03 then w ← right[p[x]] // 若 “x”是“它父节点的左孩子”,则设置 “w”为“x的叔叔”(即x为它父节点的右孩子) 04 if color[w] = RED // Case 1: x是“黑+黑”节点,x的兄弟节点是红色。(此时x的父节点和x的兄弟节点的子节点都是黑节点)。 05 then color[w] ← BLACK ▹ Case 1 // (01) 将x的兄弟节点设为“黑色”。 06 color[p[x]] ← RED ▹ Case 1 // (02) 将x的父节点设为“红色”。 07 LEFT-ROTATE(T, p[x]) ▹ Case 1 // (03) 对x的父节点进行左旋。 08 w ← right[p[x]] ▹ Case 1 // (04) 左旋后,重新设置x的兄弟节点。 09 if color[left[w]] = BLACK and color[right[w]] = BLACK // Case 2: x是“黑+黑”节点,x的兄弟节点是黑色,x的兄弟节点的两个孩子都是黑色。 10 then color[w] ← RED ▹ Case 2 // (01) 将x的兄弟节点设为“红色”。 11 x ← p[x] ▹ Case 2 // (02) 设置“x的父节点”为“新的x节点”。 12 else if color[right[w]] = BLACK // Case 3: x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的左孩子是红色,右孩子是黑色的。 13 then color[left[w]] ← BLACK ▹ Case 3 // (01) 将x兄弟节点的左孩子设为“黑色”。 14 color[w] ← RED ▹ Case 3 // (02) 将x兄弟节点设为“红色”。 15 RIGHT-ROTATE(T, w) ▹ Case 3 // (03) 对x的兄弟节点进行右旋。 16 w ← right[p[x]] ▹ Case 3 // (04) 右旋后,重新设置x的兄弟节点。 17 color[w] ← color[p[x]] ▹ Case 4 // Case 4: x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的右孩子是红色的。(01) 将x父节点颜色 赋值给 x的兄弟节点。 18 color[p[x]] ← BLACK ▹ Case 4 // (02) 将x父节点设为“黑色”。 19 color[right[w]] ← BLACK ▹ Case 4 // (03) 将x兄弟节点的右子节设为“黑色”。 20 LEFT-ROTATE(T, p[x]) ▹ Case 4 // (04) 对x的父节点进行左旋。 21 x ← root[T] ▹ Case 4 // (05) 设置“x”为“根节点”。 22 else (same as then clause with "right" and "left" exchanged) // 若 “x”是“它父节点的右孩子”,将上面的操作中“right”和“left”交换位置,然后依次执行。 23 color[x] ← BLACK
下面对删除函数进行分析。在分析之前,我们再次温习一下红黑树的几个特性:
(1) 每个节点或者是黑色,或者是红色。
(2) 根节点是黑色。
(3) 每个叶子节点是黑色。 [注意:这里叶子节点,是指为空的叶子节点!]
(4) 如果一个节点是红色的,则它的子节点必须是黑色的。
(5) 对于任意结点而言,其到叶结点树尾端NIL指针的每条路径都包含相同数目的黑结点
前面我们将"删除红黑树中的节点"大致分为两步,在第一步中"将红黑树当作一颗二叉查找树,将节点删除"后,可能违反"特性(2)、(4)、(5)"三个特性。第二步需要解决上面的三个问题,进而保持红黑树的全部特性。
为了便于分析,我们假设"x包含一个额外的黑色"(x原本的颜色还存在),这样就不会违反"特性(5)"。为什么呢?
通过RB-DELETE算法,我们知道:删除节点y之后,x占据了原来节点y的位置。 既然删除y(y是黑色),意味着减少一个黑色节点;那么,再在该位置上增加一个黑色即可。这样,当我们假设"x包含一个额外的黑色",就正好弥补了"删除y所丢失的黑色节点",也就不会违反"特性(5)"。 因此,假设"x包含一个额外的黑色"(x原本的颜色还存在),这样就不会违反"特性(5)"。
现在,x不仅包含它原本的颜色属性,x还包含一个额外的黑色。即x的颜色属性是"红+黑"或"黑+黑",它违反了"特性(1)"。
现在,我们面临的问题,由解决"违反了特性(2)、(4)、(5)三个特性"转换成了"解决违反特性(1)、(2)、(4)三个特性"。RB-DELETE-FIXUP需要做的就是通过算法恢复红黑树的特性(1)、(2)、(4)。RB-DELETE-FIXUP的思想是:将x所包含的额外的黑色不断沿树上移(向根方向移动),直到出现下面的姿态:
a) x指向一个"红+黑"节点。此时,将x设为一个"黑"节点即可。
b) x指向根。此时,将x设为一个"黑"节点即可。
c) 非前面两种姿态。
将上面的姿态,可以概括为3种情况。
① 情况说明:x是“红+黑”节点。
处理方法:直接把x设为黑色,结束。此时红黑树性质全部恢复。
② 情况说明:x是“黑+黑”节点,且x是根。
处理方法:什么都不做,结束。此时红黑树性质全部恢复。
③ 情况说明:x是“黑+黑”节点,且x不是根。
处理方法:这种情况又可以划分为4种子情况。这4种子情况如下表所示:
| 现象说明 | 处理策略 | |
| Case 1 | x是"黑+黑"节点,x的兄弟节点是红色。(此时x的父节点和x的兄弟节点的子节点都是黑节点)。 |
(01) 将x的兄弟节点设为“黑色”。 |
| Case 2 | x是“黑+黑”节点,x的兄弟节点是黑色,x的兄弟节点的两个孩子都是黑色。 |
(01) 将x的兄弟节点设为“红色”。 |
| Case 3 | x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的左孩子是红色,右孩子是黑色的。 |
(01) 将x兄弟节点的左孩子设为“黑色”。 |
| Case 4 | x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的右孩子是红色的,x的兄弟节点的左孩子任意颜色。 |
(01) 将x父节点颜色 赋值给 x的兄弟节点。 |
1. (Case 1)x是"黑+黑"节点,x的兄弟节点是红色
1.1 现象说明
x是"黑+黑"节点,x的兄弟节点是红色。(此时x的父节点和x的兄弟节点的子节点都是黑节点)。
1.2 处理策略
(01) 将x的兄弟节点设为“黑色”。
(02) 将x的父节点设为“红色”。
(03) 对x的父节点进行左旋。
(04) 左旋后,重新设置x的兄弟节点。
下面谈谈为什么要这样处理。(建议理解的时候,通过下面的图进行对比)
这样做的目的是将“Case 1”转换为“Case 2”、“Case 3”或“Case 4”,从而进行进一步的处理。对x的父节点进行左旋;左旋后,为了保持红黑树特性,就需要在左旋前“将x的兄弟节点设为黑色”,同时“将x的父节点设为红色”;左旋后,由于x的兄弟节点发生了变化,需要更新x的兄弟节点,从而进行后续处理。
1.3 示意图
2. (Case 2) x是"黑+黑"节点,x的兄弟节点是黑色,x的兄弟节点的两个孩子都是黑色
2.1 现象说明
x是“黑+黑”节点,x的兄弟节点是黑色,x的兄弟节点的两个孩子都是黑色。
2.2 处理策略
(01) 将x的兄弟节点设为“红色”。
(02) 设置“x的父节点”为“新的x节点”。
下面谈谈为什么要这样处理。(建议理解的时候,通过下面的图进行对比)
这个情况的处理思想:是将“x中多余的一个黑色属性上移(往根方向移动)”。 x是“黑+黑”节点,我们将x由“黑+黑”节点 变成 “黑”节点,多余的一个“黑”属性移到x的父节点中,即x的父节点多出了一个黑属性(若x的父节点原先是“黑”,则此时变成了“黑+黑”;若x的父节点原先时“红”,则此时变成了“红+黑”)。 此时,需要注意的是:所有经过x的分支中黑节点个数没变化;但是,所有经过x的兄弟节点的分支中黑色节点的个数增加了1(因为x的父节点多了一个黑色属性)!为了解决这个问题,我们需要将“所有经过x的兄弟节点的分支中黑色节点的个数减1”即可,那么就可以通过“将x的兄弟节点由黑色变成红色”来实现。
经过上面的步骤(将x的兄弟节点设为红色),多余的一个颜色属性(黑色)已经跑到x的父节点中。我们需要将x的父节点设为“新的x节点”进行处理。若“新的x节点”是“黑+红”,直接将“新的x节点”设为黑色,即可完全解决该问题;若“新的x节点”是“黑+黑”,则需要对“新的x节点”进行进一步处理。
2.3 示意图
3. (Case 3)x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的左孩子是红色,右孩子是黑色的
3.1 现象说明
x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的左孩子是红色,右孩子是黑色的。
3.2 处理策略
(01) 将x兄弟节点的左孩子设为“黑色”。
(02) 将x兄弟节点设为“红色”。
(03) 对x的兄弟节点进行右旋。
(04) 右旋后,重新设置x的兄弟节点。
下面谈谈为什么要这样处理。(建议理解的时候,通过下面的图进行对比)
我们处理“Case 3”的目的是为了将“Case 3”进行转换,转换成“Case 4”,从而进行进一步的处理。转换的方式是对x的兄弟节点进行右旋;为了保证右旋后,它仍然是红黑树,就需要在右旋前“将x的兄弟节点的左孩子设为黑色”,同时“将x的兄弟节点设为红色”;右旋后,由于x的兄弟节点发生了变化,需要更新x的兄弟节点,从而进行后续处理。
3.3 示意图
4. (Case 4)x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的右孩子是红色的,x的兄弟节点的左孩子任意颜色
4.1 现象说明
x是“黑+黑”节点,x的兄弟节点是黑色;x的兄弟节点的右孩子是红色的,x的兄弟节点的左孩子任意颜色。
4.2 处理策略
(01) 将x父节点颜色 赋值给 x的兄弟节点。
(02) 将x父节点设为“黑色”。
(03) 将x兄弟节点的右子节设为“黑色”。
(04) 对x的父节点进行左旋。
(05) 设置“x”为“根节点”。
下面谈谈为什么要这样处理。(建议理解的时候,通过下面的图进行对比)
我们处理“Case 4”的目的是:去掉x中额外的黑色,将x变成单独的黑色。处理的方式是“:进行颜色修改,然后对x的父节点进行左旋。下面,我们来分析是如何实现的。
为了便于说明,我们设置“当前节点”为S(Original Son),“兄弟节点”为B(Brother),“兄弟节点的左孩子”为BLS(Brother's Left Son),“兄弟节点的右孩子”为BRS(Brother's Right Son),“父节点”为F(Father)。
我们要对F进行左旋。但在左旋前,我们需要调换F和B的颜色,并设置BRS为黑色。为什么需要这里处理呢?因为左旋后,F和BLS是父子关系,而我们已知BL是红色,如果F是红色,则违背了“特性(4)”;为了解决这一问题,我们将“F设置为黑色”。 但是,F设置为黑色之后,为了保证满足“特性(5)”,即为了保证左旋之后:
第一,“同时经过根节点和S的分支的黑色节点个数不变”。
若满足“第一”,只需要S丢弃它多余的颜色即可。因为S的颜色是“黑+黑”,而左旋后“同时经过根节点和S的分支的黑色节点个数”增加了1;现在,只需将S由“黑+黑”变成单独的“黑”节点,即可满足“第一”。
第二,“同时经过根节点和BLS的分支的黑色节点数不变”。
若满足“第二”,只需要将“F的原始颜色”赋值给B即可。之前,我们已经将“F设置为黑色”(即,将B的颜色"黑色",赋值给了F)。至此,我们算是调换了F和B的颜色。
第三,“同时经过根节点和BRS的分支的黑色节点数不变”。
在“第二”已经满足的情况下,若要满足“第三”,只需要将BRS设置为“黑色”即可。
经过,上面的处理之后。红黑树的特性全部得到的满足!接着,我们将x设为根节点,就可以跳出while循环(参考伪代码);即完成了全部处理。
至此,我们就完成了Case 4的处理。理解Case 4的核心,是了解如何“去掉当前节点额外的黑色”。
4.3 示意图
OK!至此,红黑树的理论知识差不多讲完了。后续再更新红黑树的实现代码!
红黑树的java实现(完整码源)
class RBTNode
{
public boolean color; public int data; public RBTNode leftChild; public RBTNode rightChild; public RBTNode parent; public RBTNode(boolean color, int data, RBTNode leftChild, RBTNode rightChild, RBTNode parent)
{ super(); this.color = color; this.data = data; this.leftChild = leftChild; this.rightChild = rightChild; this.parent = parent; } } class RBTree
{ public RBTNode root; private static final boolean RED = false; private static final boolean BLACK=true; //前序遍历红黑树 public void preOrder(RBTNode node) { if(node != null) { System.out.print(node.data+" "); preOrder(node.leftChild); preOrder(node.rightChild); } }
public void preOrder() {this.preOrder(root);} //中序遍历红黑树 public void inOrder(RBTNode node) { if(node != null) { inOrder(node.leftChild); System.out.print(node.data+" "); inOrder(node.rightChild); } } public void inOrder() {this.inOrder(root);} //中序遍历,每个节点显示前驱和后继节点 public void testNode(RBTNode node) { if(node != null) { testNode(node.leftChild); RBTNode node1 = getPrecessor(node); RBTNode node2 = getSuccessor(node); System.out.print("本节点:"+node.data); if(node1 != null) System.out.print(" 前驱节点:"+node1.data); else System.out.print(" 没有前驱节点"); if(node2 != null) System.out.print(" 后继节点:"+node2.data); else System.out.print(" 没有后继节点"); System.out.println(""); testNode(node.rightChild); } } //后序遍历红黑树 public void postOrder(RBTNode node) { if(node != null) { postOrder(node.leftChild); postOrder(node.rightChild); System.out.print(node.data+" "); } } public void postOrder() {this.postOrder(root);} //在二叉查找树中查询给定关键字 public RBTNode find(int key) { RBTNode currentNode = this.root; while(currentNode!=null && currentNode.data!=key) { if(key < currentNode.data) currentNode = currentNode.leftChild; else currentNode = currentNode.rightChild; } return currentNode; } //查找二叉查找树中的最小关键字节点 public RBTNode minNode(RBTNode node) { if(node ==null) return null; RBTNode currentNode = node; while(currentNode.leftChild!=null) currentNode = currentNode.leftChild; return currentNode; } //查找二叉查找树中的最大关键字节点 public RBTNode maxNode(RBTNode node) { if(node ==null) return null; RBTNode currentNode = node; while(currentNode.rightChild!=null) currentNode = currentNode.rightChild; return currentNode; } //查找给定节点在中序遍历下的后继节点 private RBTNode getSuccessor(RBTNode node) { //子树为空 if(node == null) return null; //若该节点的右子树不为空,则其后继节点就是右子树中的最小关键字节点 if(node.rightChild!=null) return minNode(node.rightChild); //若该节点右子树为空,则向上一直找它的祖先,直到一个祖先是另一个祖先的左孩子 RBTNode parentNode = node.parent; while(parentNode!=null && node==parentNode.rightChild) { node = parentNode; parentNode = parentNode.parent; } return parentNode; } //查找给定节点在中序遍历下的前驱节点 public RBTNode getPrecessor(RBTNode node) { //子树为空 if(node == null) return null; //若该节点的左子树不为空,则其后继节点就是右子树中的最大关键字节点 if(node.leftChild!=null) return maxNode(node.leftChild); //若该节点左子树为空,则向上一直找它的祖先,直到一个祖先是另一个祖先的右孩子 RBTNode parentNode = node.parent; while(parentNode!=null && node == parentNode.leftChild) { node = parentNode; parentNode = parentNode.parent; } return parentNode; } /* * 对红黑树的节点(x)进行左旋转 * px px * / / * x y * / --(左旋)-. / # * lx y x ry * / / * ly ry lx ly */ public void leftRotate(RBTNode x) { //设置y为x的右孩子 RBTNode y = x.rightChild; //步骤一:如果y的左孩子非空,将y的左孩子设为x的右孩子,x设为y的左孩子的父亲 x.rightChild = y.leftChild; if(y.leftChild != null) { y.leftChild.parent = x; } //步骤二: if(x.parent == null) { this.root = y; y.parent = null; } else { //将x的父亲设为y的父亲 y.parent =x.parent; //x是其父节点的左孩子 if(x.parent.leftChild == x) x.parent.leftChild = y; //x是其父节点的右孩子 else x.parent.rightChild = y; } //步骤三:x设为y的左孩子,x的父节点设为y y.leftChild = x; x.parent = y; } /* * 对红黑树的节点(x)进行右旋转 * px px * / / * x y * / --(右旋)-. / * y rx ly x * / / * ly ry ry rx */ public void rightRotate(RBTNode x) { //设置y为x的左孩子 RBTNode y = x.leftChild; //步骤一:如果y的右孩子非空,将y的右孩子设为x的左孩子,x设为y的右孩子的父亲 x.leftChild = y.rightChild; if(y.rightChild != null) y.rightChild.parent = x; //步骤二: if(x.parent == null) { this.root = y; y.parent = null; } else { //将x的父亲设为y的父亲 y.parent =x.parent; //x是其父节点的左孩子 if(x.parent.leftChild == x) x.parent.leftChild = y; //x是其父节点的右孩子 else x.parent.rightChild = y; } //步骤三:x设为y的右孩子,y设为x的父节点 y.rightChild = x; x.parent = y; } //将节点插入到红黑树中 public void insert(RBTNode node) { if(root == null) { root = node; root.color=BLACK; return; } RBTNode currentNode = root; RBTNode parentNode = null; while(currentNode != null) { parentNode = currentNode; if(node.data < currentNode.data) currentNode = currentNode.leftChild; else if(node.data > currentNode.data) currentNode = currentNode.rightChild; else //树中已存在匹配给定关键字的节点,则什么都不做直接返回 return; } //parentNode就是最后一个非空的节点 if(node.data < parentNode.data) { parentNode.leftChild = node; node.parent = parentNode; } else { parentNode.rightChild = node; node.parent = parentNode; } //设置节点的颜色为红色 node.color = RED; //将它重新修正为一颗二叉查找树 insertFixUp(node); } public void insert(int key) { RBTNode node = new RBTNode(BLACK,key,null,null,null); if(node != null) insert(node); } /* * 红黑树插入修正函数 * 在向红黑树中插入节点之后(失去平衡),再调用该函数; * 目的是将它重新塑造成一颗红黑树。 */ public void insertFixUp(RBTNode node) { RBTNode parentNode,gparentNode; //1、父节点不存在 parentNode = node.parent; if(parentNode == null) { node.color =BLACK; return ; } //2、父节点存在且是黑色的 if(parentNode != null && (parentNode.color == BLACK)) return ; //3、若父节点存在,并且父节点的颜色是红色的 while(parentNode!=null && (parentNode.color == RED)) { //由于父节点是红色的,那么该父节点一定有父节点,因为它不能作为根节点 gparentNode = parentNode.parent; /*父节点是祖先节点的左孩子 * O G * / * O F * / * O S O S * */ if(parentNode == gparentNode.leftChild) { //Case1条件:叔叔节点是红色 RBTNode uncleNode = gparentNode.rightChild; //叔叔节点如果不为空且是红色的 if(uncleNode != null && (uncleNode.color == RED)) { uncleNode.color = BLACK; parentNode.color = BLACK; gparentNode.color = RED; //祖父节点设为当前节点 node = gparentNode; } //Case2条件:叔叔节点不为空且是黑色的或是为空(也当做是黑色的)并且当前节点是父节点的右孩子 if(((uncleNode != null && (uncleNode.color == BLACK))||uncleNode == null)
&&parentNode.rightChild == node) { leftRotate(parentNode); RBTNode temp = parentNode; parentNode = node; node = temp; } //Case3条件:叔叔节点不为空且是黑色的或是为空(也当做是黑色的)并且当前节点是父节点的左孩子 if(((uncleNode != null && (uncleNode.color == BLACK))||uncleNode == null)
&&parentNode.leftChild == node) { parentNode.color = BLACK; gparentNode.color = RED; rightRotate(gparentNode); } } /*父节点是祖先节点的右孩子 * O G * * O F * / * O S O S * */ else{ //Case1条件:叔叔节点是红色 RBTNode uncleNode = gparentNode.leftChild; //叔叔节点如果不为空且是红色的 if(uncleNode != null && (uncleNode.color == RED)) { uncleNode.color = BLACK; parentNode.color = BLACK; gparentNode.color = RED; //祖父节点设为当前节点 node = gparentNode; } //Case2条件:叔叔节点不为空且是黑色的或是为空(也当做是黑色的)并且当前节点是父节点的左孩子 if(((uncleNode != null && (uncleNode.color == BLACK))||uncleNode == null)
&&parentNode.leftChild == node) { rightRotate(parentNode); RBTNode temp = parentNode; parentNode = node; node = temp; } //Case3条件:叔叔节点不为空且是黑色的或是为空(也当做是黑色的)并且当前节点是父节点的右孩子 if(((uncleNode != null && (uncleNode.color == BLACK))||uncleNode == null)
&&parentNode.rightChild == node) { parentNode.color = BLACK; gparentNode.color = RED; leftRotate(gparentNode); } } } } //删除节点 public boolean delete(RBTNode node) { RBTNode currentNode = node; if(currentNode == null) return false; //key节点没有孩子 if(currentNode.leftChild == null && currentNode.rightChild == null) { //key节点是根节点 if(currentNode == root) { root = null; return true; } //key节点是其父节点的左孩子 RBTNode parentNode = currentNode.parent; if(currentNode ==parentNode.leftChild) { parentNode.leftChild = null; } //key节点是其父节点的右孩子 else { parentNode.rightChild = null; } return true; } //key节点只有左孩子 if(currentNode.leftChild != null && currentNode.rightChild == null) { //key节点是根节点 if(currentNode == root) { root = currentNode.leftChild; root.parent=null; return true; } //key节点是其父节点的左孩子 RBTNode parentNode = currentNode.parent; if(currentNode == parentNode.leftChild) { parentNode.leftChild = currentNode.leftChild; currentNode.leftChild.parent = parentNode; } //key节点是其父节点的右孩子 else { parentNode.rightChild = currentNode.leftChild; currentNode.leftChild.parent = parentNode; } return true; } //key节点只有右孩子 if(currentNode.leftChild == null && currentNode.rightChild != null) { //key节点是根节点 if(currentNode == root) { root = currentNode.rightChild; root.parent = null; return true; } //key节点是其父节点的左孩子 RBTNode parentNode = currentNode.parent; if(currentNode == currentNode.parent.leftChild) { parentNode.leftChild = currentNode.rightChild; currentNode.rightChild.parent = parentNode; } //key节点是其父节点的右孩子 else { parentNode.rightChild = currentNode.rightChild; currentNode.rightChild.parent = parentNode; } return true; } //key节点左右孩子都有 if(currentNode.leftChild != null && currentNode.rightChild != null) { // TreeNode successorNode = getSuccessor(currentNode); RBTNode successorNode = minNode(node.rightChild); delete(successorNode); currentNode.data = successorNode.data; } return true; } }
public class RBTreeApp { public static void main(String[] args) { int a[] = {10,40,30,60,90,70,20,50,80}; System.out.println("原始数据:"); for(int i=0;i<a.length;i++) System.out.print(a[i]+" "); System.out.println(" "); RBTree rbt = new RBTree(); for(int i=0;i<a.length;i++) rbt.insert(a[i]); System.out.println("前序遍历:"); rbt.preOrder(); System.out.println(""); System.out.println("中序遍历:"); rbt.inOrder(); System.out.println(); System.out.println("后序遍历:"); rbt.postOrder(); System.out.println(); System.out.print("根节点关键字: " ); if(rbt!=null) System.out.println(rbt.root.data); System.out.print("最小关键字: "); if(rbt.root!=null) System.out.println( rbt.minNode(rbt.root).data); System.out.print("最大关键字: "); if(rbt.root!=null) System.out.println( rbt.maxNode(rbt.root).data); System.out.println("查找节点80:"+rbt.find(80).data); rbt.testNode(rbt.root); } }
红黑树的测试结果:
原始数据:
10 40 30 60 90 70 20 50 80
前序遍历:
30 10 20 60 40 50 80 70 90
中序遍历:
10 20 30 40 50 60 70 80 90
后序遍历:
20 10 50 40 70 90 80 60 30
根节点关键字: 30
最小关键字: 10
最大关键字: 90
查找节点80:80
本节点:10 没有前驱节点 后继节点:20
本节点:20 前驱节点:10 后继节点:30
本节点:30 前驱节点:20 后继节点:40
本节点:40 前驱节点:30 后继节点:50
本节点:50 前驱节点:40 后继节点:60
本节点:60 前驱节点:50 后继节点:70
本节点:70 前驱节点:60 后继节点:80
本节点:80 前驱节点:70 后继节点:90
本节点:90 前驱节点:80 没有后继节点